Matemática
onde $\Delta$ é a área do triângulo $(T)=A_1A_2A_3$.
Demonstração: Note que:
\begin{equation}
\Delta=\frac{1}{2} a_2a_3 \text{sen}(\alpha_1)
\end{equation}
 Pela lei dos cossenos, temos que:
Pela lei dos cossenos, temos que:
\begin{equation}
\begin{matrix}
a_1^2 = a_2 ^2+a_3 ^2-2a_2 a_3 \cos (\alpha_1) \Rightarrow\\
a_2a_3 \cos(\alpha_1) = a_2^2 + a_3^2 - a_1^2\\
\end{matrix}
\end{equation}
De $(1)$ e $(2)$, temos que:
$$4\cot(\alpha_1)=\frac{2a_2a_3\cos(\alpha_1)}{\frac{1}{2}a_2a_3\text{sen}(\alpha_1)}=\frac{a_2^2+a_3^2-a_1^2}{\Delta}$$\begin{equation}
\cot(\alpha_1)=\frac{-a_1^2+a_2^2+a_3^2}{4\Delta}
\end{equation}
Por simetria, temos:
\begin{equation}
\cot(\alpha_2)=\frac{a_1^2-a_2^2+a_3^3}{4\Delta}
\end{equation}
e
\begin{equation}
\cot(\alpha_3)=\frac{a_1^2+a_2^2-a_3^2}{4\Delta}
\end{equation}
Substituindo as $(3)$, $(4)$ e $(5)$ na equação:
$$\cot (\omega)=\cot (\alpha_1)+\cot(\alpha_2)+\cot (\alpha_3)$$
(para maiores detalhes veja a parte $2$ sobre os pontos de Brocard), segue que:
$$\cot(\omega)=\frac{\left (-a_1^2+a_2^2+a_3^2 \right)+\left (a_1^2-a_2^2+a_3^2 \right )+\left (a_1^2+a_2^2-a_3^2 \right )}{4\Delta}$$
\begin{equation}
\cot(\omega)=\frac{a_1^2+a_2^2+a_3^2}{4\Delta}
\end{equation}
Teorema $4$: Em um triângulo $(T)=A_1A_2A_3$, de ângulos internos $\alpha_1$, $\alpha_2$ e $\alpha_3$ e lados opostos $a_1$, $a_2$ e $a_3$, respectivamente, contendo o ponto $\Omega$, existe o ângulo $\omega$ tal que:$$0 \leq \omega \leq \frac{\pi}{6}$$
Demonstração: Já vimos na postagem anterior que:
$$\frac{\text{sen}(\alpha_1-\omega)}{\text{sen}(\alpha_1) \cdot \text{sen}(\omega)}=\cot(\omega)-\cot(\alpha_1)$$
Substituindo $\omega$ por $-\omega$, obtemos:
\begin{matrix}
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\alpha_1) \cdot \text{sen}(-\omega)}=\frac{\cos (-\omega)}{\text{sen}(-\omega)}-\cot(\alpha_1)\\
-\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\alpha_1)\cdot \text{sen}(\omega)}=-\frac{\cos(\omega)}{\text{sen}(\omega)}-\cot(\alpha_1)\\
\\\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\text{sen}(\alpha_1)\cot(\omega)+\cos(\alpha_1)\\
\end{matrix}
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\text{sen}(\alpha_1)\left [ \cot(\alpha_1)+\cot(\alpha_2)+\cot(\alpha_3) \right ]+\cos(\alpha_1)$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\cos(\alpha_1)+\text{sen}(\alpha_1)\frac{\cos(\alpha_2)}{\text{sen}(\alpha_2)}+\text{sen}(\alpha_1)\frac{\cos(\alpha_3)}{\text{sen}(\alpha_3)}+\cos(\alpha_1)$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_2)\cos(\alpha_1)+\text{sen}(\alpha_1)\cos(\alpha_2)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_1)\cos(\alpha_3)+\text{sen}(\alpha_3)\cos(\alpha_1)}{\text{sen}(\alpha_3)}$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_1+\alpha_2)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_1+\alpha_2)}{\text{sen}(\alpha_3)}$$
Mas, $\alpha_1+\alpha_2+\alpha_3=\pi$, de modo que:
\begin{equation}
\text{sen}(\alpha_1+\alpha_2)=\text{sen}(\pi-\alpha_3)=\text{sen}(\alpha_3)
\end{equation}
e
$$\text{sen}(\alpha_1+\alpha_3)=\text{sen}(\pi-\alpha_2)=\text{sen}(\alpha_2)$$
Assim:
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_3)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_2)}{\text{sen}(\alpha_3)}$$
Pela lei dos senos no triângulo $(T)=A_1A_2A_3$, sabemos que:
$$\frac{\text{sen}(\alpha_2)}{a_2}=\frac{\text{sen}(\alpha_3)}{a_3}\Rightarrow \frac{\text{sen}(\alpha_2)}{\text{sen}(\alpha_3)}=\frac{a_2}{a_3}$$
e pela desigualdade aritmética-geométrica, segue que:
\begin{matrix}
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{a_3}{a_2}+\frac{a_2}{a_3}\\
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=2\cdot \frac{\frac{a_3}{a_2}+\frac{a_2}{a_3}}{2}\\
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)} \geq \sqrt{\frac{a_3}{a_2}\cdot \frac{a_2}{a_3}}=2\\
\end{matrix}
Isto mostra que:
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)} \geq 2$$
e a igualdade é válida se e somente se $a_2=a_3$. Consequentemente:
\begin{matrix}
2\text{sen}(\omega) \leq \text{sen}(\alpha_1+\omega) \leq 1\Rightarrow\\
0 < \text{sen}(\omega) \leq \frac{1}{2} \Rightarrow\\
0 < \omega \leq \frac{\pi}{6}\\
\end{matrix}e $\omega = \dfrac{\pi}{6}$ se e somente se $(T)$ for triângulo equilátero.
Veja mais:
Os Pontos de Brocard (Parte $1$)
Os Pontos de Brocard (Parte $2$)
Pontos Notáveis de um Triângulo
Desigualdade Aritmética-Geométrica no blog Fatos Matemáticos

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
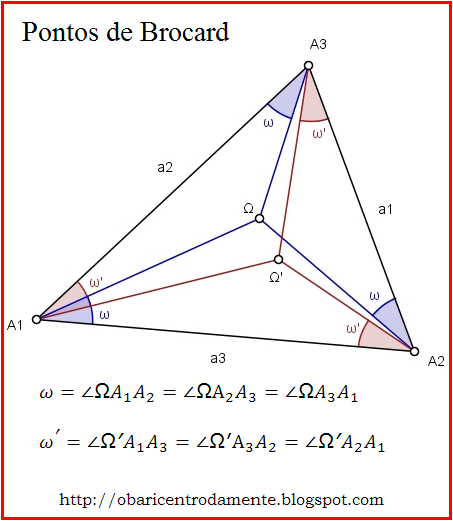
Os Pontos de Brocard (Parte 3)
Vimos na primeira postagem desta série sobre os Pontos de Brocard as definições e suas construções geométricas. Na segunda postagem, vimos algumas propriedades importantes, teoremas e corolários. Nesta terceira parte, veremos outros teoremas igualmente interessantes.
Por:
Kleber Kilhian
Paulo Sérgio C. Lino
Teorema $3$: Em um triângulo $(T)=A_1A_2A_3$, de ângulos internos, $\alpha_1$, $\alpha_2$ e $\alpha_3$, respectivamente, contendo o ponto $\Omega$ existe o ângulo $\omega$ de modo que vale a relação:
$$\cot (\omega)=\frac{\alpha_1^2+\alpha_2^2+\alpha_3^2}{4\Delta}$$onde $\Delta$ é a área do triângulo $(T)=A_1A_2A_3$.
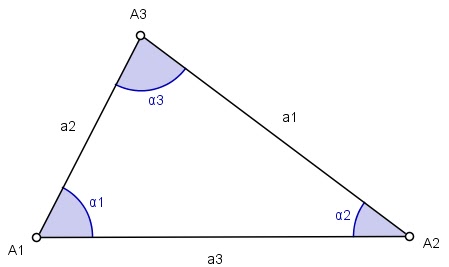
Demonstração: Note que:
\begin{equation}
\Delta=\frac{1}{2} a_2a_3 \text{sen}(\alpha_1)
\end{equation}

\begin{equation}
\begin{matrix}
a_1^2 = a_2 ^2+a_3 ^2-2a_2 a_3 \cos (\alpha_1) \Rightarrow\\
a_2a_3 \cos(\alpha_1) = a_2^2 + a_3^2 - a_1^2\\
\end{matrix}
\end{equation}
De $(1)$ e $(2)$, temos que:
$$4\cot(\alpha_1)=\frac{2a_2a_3\cos(\alpha_1)}{\frac{1}{2}a_2a_3\text{sen}(\alpha_1)}=\frac{a_2^2+a_3^2-a_1^2}{\Delta}$$\begin{equation}
\cot(\alpha_1)=\frac{-a_1^2+a_2^2+a_3^2}{4\Delta}
\end{equation}
Por simetria, temos:
\begin{equation}
\cot(\alpha_2)=\frac{a_1^2-a_2^2+a_3^3}{4\Delta}
\end{equation}
e
\begin{equation}
\cot(\alpha_3)=\frac{a_1^2+a_2^2-a_3^2}{4\Delta}
\end{equation}
Substituindo as $(3)$, $(4)$ e $(5)$ na equação:
$$\cot (\omega)=\cot (\alpha_1)+\cot(\alpha_2)+\cot (\alpha_3)$$
(para maiores detalhes veja a parte $2$ sobre os pontos de Brocard), segue que:
$$\cot(\omega)=\frac{\left (-a_1^2+a_2^2+a_3^2 \right)+\left (a_1^2-a_2^2+a_3^2 \right )+\left (a_1^2+a_2^2-a_3^2 \right )}{4\Delta}$$
\begin{equation}
\cot(\omega)=\frac{a_1^2+a_2^2+a_3^2}{4\Delta}
\end{equation}
Teorema $4$: Em um triângulo $(T)=A_1A_2A_3$, de ângulos internos $\alpha_1$, $\alpha_2$ e $\alpha_3$ e lados opostos $a_1$, $a_2$ e $a_3$, respectivamente, contendo o ponto $\Omega$, existe o ângulo $\omega$ tal que:
Demonstração: Já vimos na postagem anterior que:
$$\frac{\text{sen}(\alpha_1-\omega)}{\text{sen}(\alpha_1) \cdot \text{sen}(\omega)}=\cot(\omega)-\cot(\alpha_1)$$
Substituindo $\omega$ por $-\omega$, obtemos:
\begin{matrix}
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\alpha_1) \cdot \text{sen}(-\omega)}=\frac{\cos (-\omega)}{\text{sen}(-\omega)}-\cot(\alpha_1)\\
-\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\alpha_1)\cdot \text{sen}(\omega)}=-\frac{\cos(\omega)}{\text{sen}(\omega)}-\cot(\alpha_1)\\
\\\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\text{sen}(\alpha_1)\cot(\omega)+\cos(\alpha_1)\\
\end{matrix}
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\text{sen}(\alpha_1)\left [ \cot(\alpha_1)+\cot(\alpha_2)+\cot(\alpha_3) \right ]+\cos(\alpha_1)$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\cos(\alpha_1)+\text{sen}(\alpha_1)\frac{\cos(\alpha_2)}{\text{sen}(\alpha_2)}+\text{sen}(\alpha_1)\frac{\cos(\alpha_3)}{\text{sen}(\alpha_3)}+\cos(\alpha_1)$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_2)\cos(\alpha_1)+\text{sen}(\alpha_1)\cos(\alpha_2)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_1)\cos(\alpha_3)+\text{sen}(\alpha_3)\cos(\alpha_1)}{\text{sen}(\alpha_3)}$$
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_1+\alpha_2)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_1+\alpha_2)}{\text{sen}(\alpha_3)}$$
Mas, $\alpha_1+\alpha_2+\alpha_3=\pi$, de modo que:
\begin{equation}
\text{sen}(\alpha_1+\alpha_2)=\text{sen}(\pi-\alpha_3)=\text{sen}(\alpha_3)
\end{equation}
e
$$\text{sen}(\alpha_1+\alpha_3)=\text{sen}(\pi-\alpha_2)=\text{sen}(\alpha_2)$$
Assim:
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{\text{sen}(\alpha_3)}{\text{sen}(\alpha_2)}+\frac{\text{sen}(\alpha_2)}{\text{sen}(\alpha_3)}$$
Pela lei dos senos no triângulo $(T)=A_1A_2A_3$, sabemos que:
$$\frac{\text{sen}(\alpha_2)}{a_2}=\frac{\text{sen}(\alpha_3)}{a_3}\Rightarrow \frac{\text{sen}(\alpha_2)}{\text{sen}(\alpha_3)}=\frac{a_2}{a_3}$$
e pela desigualdade aritmética-geométrica, segue que:
\begin{matrix}
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=\frac{a_3}{a_2}+\frac{a_2}{a_3}\\
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)}=2\cdot \frac{\frac{a_3}{a_2}+\frac{a_2}{a_3}}{2}\\
\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)} \geq \sqrt{\frac{a_3}{a_2}\cdot \frac{a_2}{a_3}}=2\\
\end{matrix}
Isto mostra que:
$$\frac{\text{sen}(\alpha_1+\omega)}{\text{sen}(\omega)} \geq 2$$
e a igualdade é válida se e somente se $a_2=a_3$. Consequentemente:
\begin{matrix}
2\text{sen}(\omega) \leq \text{sen}(\alpha_1+\omega) \leq 1\Rightarrow\\
0 < \text{sen}(\omega) \leq \frac{1}{2} \Rightarrow\\
0 < \omega \leq \frac{\pi}{6}\\
\end{matrix}e $\omega = \dfrac{\pi}{6}$ se e somente se $(T)$ for triângulo equilátero.
Veja mais:
Os Pontos de Brocard (Parte $1$)
Os Pontos de Brocard (Parte $2$)
Pontos Notáveis de um Triângulo
Desigualdade Aritmética-Geométrica no blog Fatos Matemáticos

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
