Matemática
- Polinómios
Divisão inteira de polinómios Calcule o quociente e o resto da divisão inteira de A(x) = 4x3 + 8x2 + 1 por B(x) = 2x2 + 3x - 1.Resolução: Recorde que o algoritmo da divisão inteira de polinómios permite calcular o quociente e o resto da...
- Divisão De Polinômios
Divisão de polinômios Definição Considere dois polinômios: A(x) denominado dividendo e B(x) denominado divisor, com B(x) ≠ 0. Na divisão de A por B obtemos a função polinomial Q, denominada quociente, e a função polinomial R denominada resto,...
- Polinômios - Exercícios Resolvidos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Polinômios
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Divisão De Polinômios
Considere dois polinômios, A(x) e B(x), sendo B(x) um polinômio não identicamente nulo. Ao dividir A(x) por B(x) encontramos outros dois polinômios Q(x) e R(x), tais que: Onde: A(x) é o dividendo B(x) é o divisor Q(x) é o quociente R(x) é o resto...
Matemática
Polinômios
Considerações sobre o Grau Sendo A e B dois polinômios não-nulos, o grau do produto A · B é a soma dos graus dos polinômios A e B. 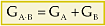 No caso de um dos polinômios A ou B ser identicamente nulo, o produto A · B é identicamente nulo (o grau não é definido). Exemplo GA = 5 e GB = 3 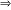 GA + B = 8 GA + B = 87. Divisão de Polinômios 7.1. Definição Dados dois polinômios, A(x) e B(x), B não-nulo, existe um único par de polinômios Q (x) e R(x) em que se verificam as condições: 1a) A(x) 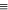 B(x) · Q(x)+ R(x) B(x) · Q(x)+ R(x)2a) GR < GB ou R(x) 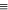 0 0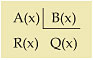  Os polinômios A e B são chamados de dividendoe divisor e os polinômios Q e R são o quociente e oresto. Quando R(x)  0 , dizemos que a divisão é exata, ou que A(x) é divisível por B(x). 0 , dizemos que a divisão é exata, ou que A(x) é divisível por B(x).7.2. O Método da Chave Dividir o polinômio A(x) pelo polinômio B(x), não-nulo, significa determinar o quociente Q(x) e o resto R(x). Vamos dividir, por exemplo, o polinômio A(x) = 2x3 – 8x2 +7x – 5 por B(x) = x2 – 2x + 3, pelo método da chave. 1a etapa Dividimos inicialmente 2x3 por x2, encontrando 2x. 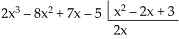  2a etapa Multiplicamos 2x por x2 – 2x + 3 e vemos “quanto falta para 2x3 – 8x2 + 7x – 5”, isto é, subtraímos: |  |  |  | 2x3 – 4x2 + 6x de 2x3 – 8x2 + 7x – 5. 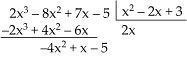 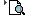 3a etapa Enquanto o grau do resto for maior ou igual ao grau do divisor, continuamos a divisão. Dividimos então – 4x2 por x2, encontrando – 4. 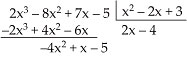 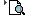 4a etapa Multiplicamos – 4 por x2 – 2x + 3 e vemos “quanto falta para – 4x2 + x – 5”. 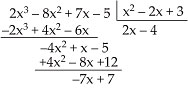  Nesse ponto terminamos a divisão, pois o grau de – 7x + 7 é menor que o grau do divisor. Portanto, temos: Quociente = Q(x) = 2x – 4 Resto = R(x) = – 7x + 7 7.3. Considerações sobre o Grau Sendo A e B dois polinômios não-nulos, o grau do quociente Q(x) é a diferença entre os graus dos polinômios A e B, e o resto, se não for nulo, terá grau menor que o grau de B(x). 7.4. O Método de Descartes Vamos dividir, por exemplo, o polinômio A (x) = 2x3 – 8x2 + 7x – 5 por B(x) = x2 – 2x + 3 pelo método de Descartes, também conhecido como método dos coeficientes a determinar. 1a etapa Estimamos quem serão o quociente Q(x) e o resto R(x) da divisão, lembrando que GQ = GA – GB = 1, e, se o resto não for nulo, GR < GBinterna.coceducacao.com.br |
- Polinómios
Divisão inteira de polinómios Calcule o quociente e o resto da divisão inteira de A(x) = 4x3 + 8x2 + 1 por B(x) = 2x2 + 3x - 1.Resolução: Recorde que o algoritmo da divisão inteira de polinómios permite calcular o quociente e o resto da...
- Divisão De Polinômios
Divisão de polinômios Definição Considere dois polinômios: A(x) denominado dividendo e B(x) denominado divisor, com B(x) ≠ 0. Na divisão de A por B obtemos a função polinomial Q, denominada quociente, e a função polinomial R denominada resto,...
- Polinômios - Exercícios Resolvidos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Polinômios
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Divisão De Polinômios
Considere dois polinômios, A(x) e B(x), sendo B(x) um polinômio não identicamente nulo. Ao dividir A(x) por B(x) encontramos outros dois polinômios Q(x) e R(x), tais que: Onde: A(x) é o dividendo B(x) é o divisor Q(x) é o quociente R(x) é o resto...
