Matemática
 Quando eu era criança fui à praia para um dia de lazer, sempre fui muito curioso e sempre queria ter uma explicação para todas as coisas (talvez isso me motivou escolher a Matemática), dessa vez me deparei com a Linha do Horizonte e me perguntei:
Quando eu era criança fui à praia para um dia de lazer, sempre fui muito curioso e sempre queria ter uma explicação para todas as coisas (talvez isso me motivou escolher a Matemática), dessa vez me deparei com a Linha do Horizonte e me perguntei:
- Qual a distância da beira da praia até a linha do horizonte?
Fiquei bastante intrigado, até perguntei pra algumas pessoas, mas elas não souberam me responder naquele momento, resolvi então deixar para depois, pensei que no futuro talvez soubesse a resposta para essa dúvida. Os anos passaram e no último sábado estava em minha casa navegando na Internet e me deparei com a imagem do início dessa postagem e novamente me veio a pergunta não respondida da minha infância, mas dessa vez sabia que eu mesmo podia chegar ao resultado, e é essa experiência que compartilho hoje com os leitores do Giga Matemática.
Primeiramente, o que é a linha do horizonte? Eis a definição de alguns dicionários:
"1. Lugar em que céu e terra parecem que se unem.
2. Linha que se estende até onde alcança o olhar.
3. Toda faixa de mar, céu ou terra que pode ser vista por alguém em campo aberto."
Usaremos aqui a definição 2. Note que pela definição 3, fatores na paisagem alteram a distância da linha do horizonte, tais como elevações, vegetação, construções, etc. Desse modo, nos focaremos em uma situação particular, onde o observador está visualizando o mar.
Vou listar abaixo algumas perguntas que serão respondidas ao final da postagem:
 Ora, o Horizonte nada mais é do que um efeito visual gerado pela curvatura da Terra, ou seja, a linha do horizonte depende de "quão curva" a terra é, assim iremos assumir que a Terra é uma Esfera de raio $R$ ($R\approx 6378,1 km$). Se traçarmos um segmento de reta partindo de nossos olhos e tangenciando a superfície da terra então podemos definir a distância $D$ que a linha do horizonte de encontra de nossos olhos, então um dos fatores que irá influenciar no cálculo dessa distância será a altura $h$ que nossos olhos se encontram do chão.
Ora, o Horizonte nada mais é do que um efeito visual gerado pela curvatura da Terra, ou seja, a linha do horizonte depende de "quão curva" a terra é, assim iremos assumir que a Terra é uma Esfera de raio $R$ ($R\approx 6378,1 km$). Se traçarmos um segmento de reta partindo de nossos olhos e tangenciando a superfície da terra então podemos definir a distância $D$ que a linha do horizonte de encontra de nossos olhos, então um dos fatores que irá influenciar no cálculo dessa distância será a altura $h$ que nossos olhos se encontram do chão.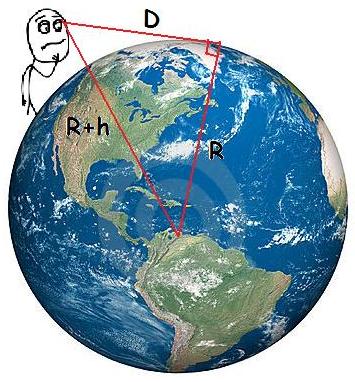
- Questão 56 ? Concurso See ? 2.010 ? Professor De Educação Básica Ii ? Matemática
A figura representa o planeta Terra e uma montanha cujo ponto mais alto é indicado por A. A semi-reta AB indica a linha do horizonte, e o segmento BC o raio da Terra. Se BC = 100 . AB, então, a altura da montanha, na mesma unidade de BC e AB, é igual...
- Video Da Postagem "qual A Distância Até A Linha Do Horizonte?"
Olá pessoal, a postagem hoje é para divulgar o resultado de uma parceria do Giga Matemática com o blog Matemática Rio. No vídeo é apresentado a postagem Qual a distância da linha do horizonte?. Visualizem abaixo: Não deixem de visitar o...
- Trigonométria
1) Calcular os catetos de um triângulo retângulo cuja hipotenusa mede 6 cm e um dos ângulos mede 60º. 2) Quando o ângulo de elevação do sol é de 65 º, a sombra de um edifício mede 18 m. Calcule a altura do edifício. (sen 65º = 0,9063, cos...
- Distância Entre Ponto E Reta
Considere um ponto A (x0, y0) e uma reta s: ax + by + c = 0 pertencente a um mesmo plano, a distância desses pontos poderá ser calculada através da fórmula: Exemplo 1: Calcule a distância da reta P à reta r, em cada um dos casos: • P(1,3) e r:...
- Posição Relativa Entre Uma Reta E Uma Circunferência
Posição relativa entre uma reta e uma circunferênciaMarcelo Rigonatto CircunferênciaConsidere uma circunferência no plano de cento O(xo, yo) e raio r. Dada uma reta s de equação ax + by +c = 0, também do mesmo plano. A reta...
Matemática
Qual a "distância" da Linha do Horizonte?
- Qual a distância da beira da praia até a linha do horizonte?
Fiquei bastante intrigado, até perguntei pra algumas pessoas, mas elas não souberam me responder naquele momento, resolvi então deixar para depois, pensei que no futuro talvez soubesse a resposta para essa dúvida. Os anos passaram e no último sábado estava em minha casa navegando na Internet e me deparei com a imagem do início dessa postagem e novamente me veio a pergunta não respondida da minha infância, mas dessa vez sabia que eu mesmo podia chegar ao resultado, e é essa experiência que compartilho hoje com os leitores do Giga Matemática.
Primeiramente, o que é a linha do horizonte? Eis a definição de alguns dicionários:
"1. Lugar em que céu e terra parecem que se unem.
2. Linha que se estende até onde alcança o olhar.
3. Toda faixa de mar, céu ou terra que pode ser vista por alguém em campo aberto."
Usaremos aqui a definição 2. Note que pela definição 3, fatores na paisagem alteram a distância da linha do horizonte, tais como elevações, vegetação, construções, etc. Desse modo, nos focaremos em uma situação particular, onde o observador está visualizando o mar.
Vou listar abaixo algumas perguntas que serão respondidas ao final da postagem:
- A altura da pessoa altera a distância do horizonte?
- A elevação em relação ao nível do mar altera essa distância?
- A curvatura da Terra influencia essa distância?
- Qual seria então a distância da Linha do Horizonte em outros planetas?

 Ora, o Horizonte nada mais é do que um efeito visual gerado pela curvatura da Terra, ou seja, a linha do horizonte depende de "quão curva" a terra é, assim iremos assumir que a Terra é uma Esfera de raio $R$ ($R\approx 6378,1 km$). Se traçarmos um segmento de reta partindo de nossos olhos e tangenciando a superfície da terra então podemos definir a distância $D$ que a linha do horizonte de encontra de nossos olhos, então um dos fatores que irá influenciar no cálculo dessa distância será a altura $h$ que nossos olhos se encontram do chão.
Ora, o Horizonte nada mais é do que um efeito visual gerado pela curvatura da Terra, ou seja, a linha do horizonte depende de "quão curva" a terra é, assim iremos assumir que a Terra é uma Esfera de raio $R$ ($R\approx 6378,1 km$). Se traçarmos um segmento de reta partindo de nossos olhos e tangenciando a superfície da terra então podemos definir a distância $D$ que a linha do horizonte de encontra de nossos olhos, então um dos fatores que irá influenciar no cálculo dessa distância será a altura $h$ que nossos olhos se encontram do chão.Então três medidas estarão envolvidas:
- O raio da terra $(R)$;
- A altura do observador $(h)$;
- A distância da Linha do Horizonte $(D)$.

A figura acima mostra um esquema de como podemos obter essa distância, note que o segmento de reta de comprimento $D$ é perpendicular ao raio da Terra, pois a reta à qual contém esse segmento tangencia um grande círculo da terra. Utilizando um Milenar Teorema da Geometria advindo da Escola Pitagórica, conhecido também por Teorema de Pitágoras (risos), temos a solução para nossos problemas:
$$(R+h)^2=R^2+D^2$$
$$R^2+2hR+h^2=R^2+D^2$$
$$2hR+h^2=D^2$$
$$D=\sqrt{h^2+2hR}$$
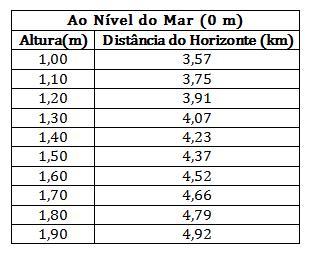
Podemos considerar a distância do horizonte como uma função que depende do valor de $h$, ou seja, a distância depende da altura que o observador se encontra em relação ao nível do mar. A tabela abaixo mostra alguns valores para algumas alturas:

À medida que nos elevamos do nível do mar, a distância da Linha do Horizonte aumenta, ou seja, a Linha do Horizonte da minha infância agora está mais longe! Antes era em torno de 4,37 km, hoje é 4,66 km.
Iremos agora responder as perguntas formuladas começo da postagem:
1. A altura da pessoa altera a distância do horizonte?
Acabamos de ver que sim, pois o cálculo dessa distância depende da altura $h$ que os olhos do observador se encontra do nível do mar.
2. A elevação em relação ao nível do mar altera essa distância?
Sim, nesse caso a fórmula ficaria da seguinte forma:
$$D=\sqrt{(h+a)^2+2(h+a)R}$$
onde, $h$ é a altura da pessoa, $a$ é a elevação em relação ao nível do mar e $R$ é o raio da Terra em metros.
Por exemplo, uma pessoa de 1,80 m (em média, os olhos se encontram à 10 cm do topo da cabela, por isso aqui será usado $h=1,70$) que está no alto de uma montanha com 50 m de altura do nível do mar ($a=50$)irá enxergar o horizonte à uma distância de aproximadamente 25,51 km.
3. A curvatura da Terra influencia essa distância?
Este é um conceito de Geometria Diferencial, a curvatura gaussiana $K$ de uma esfera depende do raio da esfera considerada, de fato, $K=\frac{1}{R^2}$, assim, em alguns pontos da Terra o horizonte está mais perto ou mais longe, perto da Linha do Equador o horizonte está mais perto do que próximo ao pólos, mas a diferença é muito pequena.
4. Qual seria então a distância da Linha do Horizonte em outros planetas?
Nesse caso a fórmula ficaria da seguinte forma:
$$D=\sqrt{(h+a)^2+2(h+a)R_p}$$
onde, $h$ é altura dos olhos do observador ao solo, $a$ é a altitude em relação ao ponto mais baixo do planeta(não considerando crateras) e $R_p$ é o raio do planeta considerado.
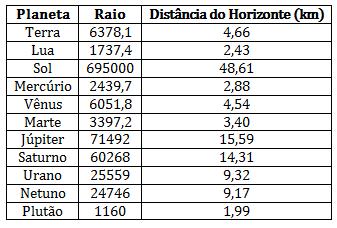
Note que essa fórmula é bem geral, a tabela abaixo mostra a distância do horizonte em alguns planetas, na lua e no sol. (Consideraremos uma pessoa de 1,80 m de altura, com os olhos à uma distância de 1,70 m do solo e no ponto mais baixo do planeta).

Encerro esta postagem deixando a célebre frase de Isaac Newton que agora faz todo sentido (risos):
"Se pude enxergar mais longe, é porque me apoiei nos ombros de gigantes".
- Questão 56 ? Concurso See ? 2.010 ? Professor De Educação Básica Ii ? Matemática
A figura representa o planeta Terra e uma montanha cujo ponto mais alto é indicado por A. A semi-reta AB indica a linha do horizonte, e o segmento BC o raio da Terra. Se BC = 100 . AB, então, a altura da montanha, na mesma unidade de BC e AB, é igual...
- Video Da Postagem "qual A Distância Até A Linha Do Horizonte?"
Olá pessoal, a postagem hoje é para divulgar o resultado de uma parceria do Giga Matemática com o blog Matemática Rio. No vídeo é apresentado a postagem Qual a distância da linha do horizonte?. Visualizem abaixo: Não deixem de visitar o...
- Trigonométria
1) Calcular os catetos de um triângulo retângulo cuja hipotenusa mede 6 cm e um dos ângulos mede 60º. 2) Quando o ângulo de elevação do sol é de 65 º, a sombra de um edifício mede 18 m. Calcule a altura do edifício. (sen 65º = 0,9063, cos...
- Distância Entre Ponto E Reta
Considere um ponto A (x0, y0) e uma reta s: ax + by + c = 0 pertencente a um mesmo plano, a distância desses pontos poderá ser calculada através da fórmula: Exemplo 1: Calcule a distância da reta P à reta r, em cada um dos casos: • P(1,3) e r:...
- Posição Relativa Entre Uma Reta E Uma Circunferência
Posição relativa entre uma reta e uma circunferênciaMarcelo Rigonatto CircunferênciaConsidere uma circunferência no plano de cento O(xo, yo) e raio r. Dada uma reta s de equação ax + by +c = 0, também do mesmo plano. A reta...
