Matemática
Regra de Chió
Através dessa regra é possível abaixar em uma unidade a ordem de uma matriz quadrada A sem alterar o valor do seu determinante.
A regra prática de Chió consiste em:
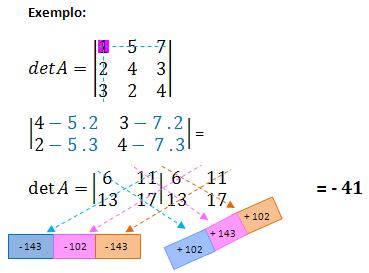
a) Escolher um elemento aij = 1 (caso não exista, aplicar as propriedades para que apareça o elemento 1).
b) Suprimir a linha (i) e a coluna (j) do elemento aij = 1, obtendo-se o menor complementar do referido elemento.
c) Subtrair de cada elemento do menor complementar obtido o produto dos elementos que ficam nos pés das perpendiculares traçadas do elemento considerado às filas suprimidas.
d) Multiplicar o determinante obtido no 3.º item por (-1)i+j onde i e j designam as ordens da linha e da coluna às quais pertence o elemento aij = 1.
www.colegioweb.com.br
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Matriz
Para compreender melhor o que é uma matriz, iremos compará-la com uma tabela. Toda tabela é formada por linhas e colunas, assim como uma matriz. Na matriz indicamos a quantidade de linhas por m e a quantidade de colunas por n. Tanto em uma tabela como...
- Cálculo Do Cofator De Uma Matriz Quadrada
Cálculo do cofator de uma matriz quadradaMarcelo Rigonatto MatrizO cálculo do determinante de uma matriz quadrada, muitas vezes, pode ser simplificado utilizando algumas propriedades e teoremas. O cofator é um elemento que facilitará...
- Determinante
a) Menor complementar O menor complementar de um elemento é o determinante da sua matriz quadrada. Para obtermos o menor complementar basta eliminar a linha e a coluna que o elemento pertence. Obs.: todos elementos de uma matriz possui um menor complementar....
- A Regra De Chió Para O Cálculo De Determinantes
Toda matriz quadrada, de qualquer ordem, tem associada a ela um número chamado determinante da matriz. Existem alguns métodos para calcular o determinante de uma matriz, como por exemplo a Regra de Sarrus e o Teorema de Laplace utilizando a Matriz de...
Matemática
Regra de chió
Regra de Chió
Através dessa regra é possível abaixar em uma unidade a ordem de uma matriz quadrada A sem alterar o valor do seu determinante.
A regra prática de Chió consiste em:
a) Escolher um elemento aij = 1 (caso não exista, aplicar as propriedades para que apareça o elemento 1).
b) Suprimir a linha (i) e a coluna (j) do elemento aij = 1, obtendo-se o menor complementar do referido elemento.
c) Subtrair de cada elemento do menor complementar obtido o produto dos elementos que ficam nos pés das perpendiculares traçadas do elemento considerado às filas suprimidas.
d) Multiplicar o determinante obtido no 3.º item por (-1)i+j onde i e j designam as ordens da linha e da coluna às quais pertence o elemento aij = 1.

www.colegioweb.com.br
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Matriz
Para compreender melhor o que é uma matriz, iremos compará-la com uma tabela. Toda tabela é formada por linhas e colunas, assim como uma matriz. Na matriz indicamos a quantidade de linhas por m e a quantidade de colunas por n. Tanto em uma tabela como...
- Cálculo Do Cofator De Uma Matriz Quadrada
Cálculo do cofator de uma matriz quadradaMarcelo Rigonatto MatrizO cálculo do determinante de uma matriz quadrada, muitas vezes, pode ser simplificado utilizando algumas propriedades e teoremas. O cofator é um elemento que facilitará...
- Determinante
a) Menor complementar O menor complementar de um elemento é o determinante da sua matriz quadrada. Para obtermos o menor complementar basta eliminar a linha e a coluna que o elemento pertence. Obs.: todos elementos de uma matriz possui um menor complementar....
- A Regra De Chió Para O Cálculo De Determinantes
Toda matriz quadrada, de qualquer ordem, tem associada a ela um número chamado determinante da matriz. Existem alguns métodos para calcular o determinante de uma matriz, como por exemplo a Regra de Sarrus e o Teorema de Laplace utilizando a Matriz de...
