Matemática
Toda matriz quadrada, de qualquer ordem, tem associada a ela um número chamado determinante da matriz.
Existem alguns métodos para calcular o determinante de uma matriz, como por exemplo a Regra de Sarrus e o Teorema de Laplace utilizando a Matriz de Cofatores.
A Regra de Chió é muito prática se o elemento $a_{11}$ da matriz for igual a $1$, o que nos permite calcular o determinante de uma matriz de ordem $n$ usando uma matriz de ordem $n-1$.
Dada uma matriz quadrada de ordem $n$ sendo $a_{11}=1$:
\begin{equation*}
\begin{bmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
a_{21} & a_{22} & a_{23} & \cdots & a_{2n}\\
a_{31} & a_{32} & a_{33} & \cdots & a_{3n}\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn}
\end{bmatrix}
\end{equation*}
obtemos uma matriz de ordem $n-1$ fazendo:
\begin{equation*}
\begin{bmatrix}
a_{22}-(a_{12}\cdot a_{21}) & a_{23}-(a_{13}\cdot a_{21}) & \cdots & a_{2n}-(a_{1n}\cdot a_{21})\\
a_{32}-(a_{12}\cdot a_{31}) & a_{33}-(a_{13}\cdot a_{31}) & \cdots &a_{3n}-(a_{1n}\cdot a_{31}) \\
\vdots & \vdots & \ddots & \vdots\\
a_{n2}-(a_{12}\cdot a_{n1}) & a_{n3}-(a_{13}\cdot a_{n1}) & \cdots & a_{nn}-(a_{1n}\cdot a_{n1})
\end{bmatrix}
\end{equation*}
\begin{equation*}
M=
\begin{bmatrix}
1 & 2 & 0 & -1\\
1 & 3 & 6 & 9\\
4 & 1 & 2 & 0\\
-2 & 2 & 3 & -4
\end{bmatrix}
\end{equation*}
Como o elemento $a_{11}=1$, então fazemos:
\begin{equation*}
\det{M}=
\begin{vmatrix}
\boldsymbol {\color{red}{1}} & \boldsymbol{\color{blue}{2}} & \boldsymbol{\color{blue}{0}} & \boldsymbol{\color{blue}{-1}}\\
\boldsymbol{\color{green}{1}} & 3 & 6 & 9\\
\boldsymbol{\color{green}{4}} & 1 & 2 & 0\\
\boldsymbol{\color{green}{-2}} & 2 & 3 & -4
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
3-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{1}}) & 6-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{1}}) & 9-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{1}})\\
1-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{4}})& 2-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{4}}) & 0-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{4}})\\
2-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{(-2)}}) & 3-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{(-2)}}) & -4-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{(-2)}})
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
1 & 6 & 10\\
-7 & 2 & 4\\
6 & 3 & -6
\end{vmatrix}
\end{equation*}
Aqui poderíamos aplicar a Regra de Sarrus, mas vamos aplicar novamente a Regra de Chió, já que o elemento $a_{11}=1$ e assim obteremos um determinante a partir de uma matriz de ordem $2$, resolvido rapidamente.
\begin{equation*}
\det{M}=
\begin{vmatrix}
\boldsymbol {\color{red}{1}} & \boldsymbol{\color{blue}{6}} & \boldsymbol{\color{blue}{10}} \\
\boldsymbol{\color{green}{-7}} & 2 & 4 \\
\boldsymbol{\color{green}{6}} & 3 & -6
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
2-(\boldsymbol {\color{blue}{6}} \cdot \boldsymbol {\color{green}{(-7)}}) & 4-(\boldsymbol {\color{blue}{10}} \cdot \boldsymbol {\color{green}{(-7)}}) \\
3-(\boldsymbol {\color{blue}{6}} \cdot \boldsymbol {\color{green}{(6)}}) & -6-(\boldsymbol {\color{blue}{10}} \cdot \boldsymbol {\color{green}{(6)}})
\end{vmatrix}
\\
\:
\
\det{M}=
\begin{vmatrix}
44 & 74\\
-33 & -66
\end{vmatrix}
\\
\:
\\
\det{M}=(44 \cdot (-66)) - (74 \cdot (-33))=-462
\end{equation*}
Assim, o determinante da matriz $M$ é igual a $-462$.
Ao trocarmos de posição duas filas de uma matriz, o determinante da nova matriz é o oposto do determinante da matriz anterior, ou seja, tem o sinal trocado.
Por exemplo: seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
3 & 2 & 0 &-1\\
2 & 3 & 6 &9\\
4 & 1 & 2 &0\\
-2 & 2 & 3 &-1
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}\det{A}=
\begin{vmatrix}
3 & 2 & 0 &-1\\
2 & 3 & 6 &9\\
4 & 1 & 2 &0\\
-2 & 2 & 3 &-1
\end{vmatrix}
\end{equation*}
Trocando a primeira linha pela terceira, obtemos:
\begin{equation*}\det{A}=-
\begin{vmatrix}
4 & 1 & 2 &0\\
2 & 3 & 6 &9\\
3 & 2 & 0 & -1\\
-2 & 2 & 3 &-1
\end{vmatrix}
\end{equation*}
E agora trocamos a primeira coluna pela segunda:
\begin{equation*}\det{A}=
\begin{vmatrix}
1 & 4 & 2 &0\\
3 & 2 & 6 &9\\
2 & 3 & 0 & -1\\
2 & -2 & 3 &-1
\end{vmatrix}
\end{equation*}
Vejam que o sinal do determinante passou de $+$ para $-$ e depois para $+$.
$2)$ Se o elemento $a_{11} \neq 1$ e n]ao houver qualquer elemento da matriz igual a $1$, podemos criar elementos igual a $1$ na matriz usando o Teorema de Jacobi que essencialmente diz que o determinante de uma matriz quadrada não se altera se adicionarmos aos elementos de uma fila qualquer, os elementos correspondentes de outra fila paralela previamente multiplicada por uma constante.
Por exemplo: Seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
3 & 2 & 0 & -1\\
2 & 3 & 6 & 9\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}
\det A=\begin{vmatrix}
3 & 2 & 0 & -1\\
2 & 3 & 6 & 9\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{vmatrix}
\end{equation*}
Como não há um elemento da matriz igual a $1$, vamos criá-lo multiplicando a segunda linha por $-1$ e somá-la à primeira:
\begin{equation*}
\det A=\begin{vmatrix}
3 & 2 & 0 & -1\\
\boldsymbol{\color{red}{2}} & \boldsymbol{\color{red}{3}} & \boldsymbol{\color{red}{6}} & \boldsymbol{\color{red}{9}}\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{vmatrix}
\begin{matrix}
\longleftarrow & + & \looparrowleft \\
\longrightarrow & \times &(-1) \\
~\\
~\\
\end{matrix}
=
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{-6}}&\boldsymbol{\color{blue}{-10}}\\
2&3&6&9\\
4&5&2&0\\
-2&2&3&-4
\end{vmatrix}
\end{equation*}
Ao calcularmos o determinante da matriz equivalente, veremos que é igual ao determinante da matriz original.
$3)$ Se o elemento $a_{11} \neq 1$ e não houver outro elemento igual a $1$ na matriz, podemos criar elementos igual a $1$ na matriz colocando um fator $k$ comum a uma fila em evidência, pois se todos os elementos de uma fila de uma matriz quadrada são multiplicados por um mesmo número $k$, então seu determinante fica multiplicado por $k$.
Por exemplo: Seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
2&4&-2\\
10&6&0\\
4&-4&10
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}
\det A=
\begin{vmatrix}
\boldsymbol{\color{red}{2}}&\boldsymbol{\color{red}{4}}&\boldsymbol{\color{red}{-2}}\\
10&6&0\\
4&-4&10
\end{vmatrix}
=
2
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&\boldsymbol{\color{blue}{2}}&\boldsymbol{\color{blue}{-1}}\\
10&6&0\\
4&-4&10
\end{vmatrix}
\end{equation*}
\begin{equation*}
M=
\begin{bmatrix}
2&-1&0&3&2\\
-2&3&2&0&-2\\
-3&2&-1&-5&4\\
-1&3&2&-2&0\\
0&4&-2&-1&3
\end{bmatrix}
\end{equation*}
Nesta matriz, o elemento $a_{11}\neq 1$ e não há nenhum outro elemento da matriz que seja igual a $1$. Para que o elemento $a_{11}$ seja igual a $1$, multiplicamos a segunda coluna por $1$ e somamos o resultado com a primeira coluna:
\begin{equation*}
\det M=
\begin{vmatrix}
2&\boldsymbol{\color{red}{-1}}&0&3&2\\
-2&\boldsymbol{\color{red}{3}}&2&0&-2\\
-3&\boldsymbol{\color{red}{2}}&-1&-5&4\\
-1&\boldsymbol{\color{red}{3}}&2&-2&0\\
0&\boldsymbol{\color{red}{4}}&-2&-1&3
\end{vmatrix}
=
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&-1&0&3&2\\
\boldsymbol{\color{blue}{1}}&3&2&0&-2\\
\boldsymbol{\color{blue}{-1}}&2&-1&-5&4\\
\boldsymbol{\color{blue}{2}}&3&2&-2&0\\
\boldsymbol{\color{blue}{4}}&4&-2&-1&3
\end{vmatrix}
\end{equation*}
Agora, podemos aplicar a Regra de Chió:
\begin{equation*}
\det M=
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{0}}&\boldsymbol{\color{blue}{3}}&\boldsymbol{\color{blue}{2}}\\
\boldsymbol{\color{green}{1}}&3&2&0&-2\\
\boldsymbol{\color{green}{-1}}&2&-1&-5&4\\
\boldsymbol{\color{green}{2}}&3&2&-2&0\\
\boldsymbol{\color{green}{4}}&4&-2&-1&3
\end{vmatrix}
\\
\:
\\
=
\begin{vmatrix}
3-(\color{blue}{-1}\cdot \color{green}{1}) & 2-(\color{blue}{0}\cdot \color{green}{1}) & 0-(\color{blue}{3}\cdot \color{green}{1}) & -2-(\color{blue}{2}\cdot \color{green}{1})\\
2-(\color{blue}{-1}\cdot \color{green}{(-1)}) & -1-(\color{blue}{0}\cdot \color{green}{(-1)}) & -5-(\color{blue}{3}\cdot \color{green}{(-1)}) & 4-(\color{blue}{2}\cdot \color{green}{(-1)})\\
3-(\color{blue}{-1}\cdot \color{green}{2}) & 2-(\color{blue}{0}\cdot \color{green}{2}) & -2-(\color{blue}{3}\cdot \color{green}{2}) &0-(\color{blue}{2}\cdot \color{green}{2})\\
4-(\color{blue}{-1}\cdot \color{green}{4}) & -2-(\color{blue}{0}\cdot \color{green}{4}) & -1-(\color{blue}{3}\cdot \color{green}{4}) & 3-(\color{blue}{2}\cdot \color{green}{4})
\end{vmatrix}
\\
\:
\\
=
\begin{vmatrix}
4&2&-3&-4\\
1&-1&-2&6\\
5&2&-8&-4\\
8&-2&-13&-5
\end{vmatrix}
\end{equation*}
Agora, trocamos a segunda linha pela primeira e aplicamos a Regra de Chió novamente. Como estaremos trocando apenas um linha, não podemos nos esquecer de trocar o sinal do determinante:
\begin{equation*}
\det M=-
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{-2}}&\boldsymbol{\color{blue}{6}}\\
\boldsymbol{\color{green}{4}}&2&-3&-4\\
\boldsymbol{\color{green}{5}}&2&-8&-4\\
\boldsymbol{\color{green}{8}}&-2&-13&-5
\end{vmatrix}
\\
\:
\\
=-
\begin{vmatrix}
2-(-1\cdot 4) & -3-(-2\cdot 4) & -4-(6\cdot 4)\\
2-(-1 \cdot 5) & -8-(-2 \cdot 5) & -4-(6 \cdot 5)\\
-2-(-1\cdot 8) & -13-(-2\cdot8) & -5-(6\cdot8)
\end{vmatrix}
\\
\:
\\
=-
\begin{vmatrix}
6&5&-28\\
7&2&-34\\
6&3&-53
\end{vmatrix}
\end{equation*}
Aqui, podemos aplicar a Regra de Sarrus ou ainda aplica a Regra de Chió novamente. Primeiramente trocamos a segunda linha pela primeira, já trocando o sinal do determinante:
\begin{equation*}
\det M=
\begin{vmatrix}
7&2&-34\\
6&5&-28\\
6&3&-53
\end{vmatrix}
\end{equation*}
Agora, multiplicamos a segunda linha por $-1$ e somamos o resultado à primeira linha:
\begin{equation*}
\det M=
\begin{vmatrix}
1&-3&-6\\
6&5&-28\\
6&3&-53
\end{vmatrix}
\end{equation*}
Agora que o elemento $a_{11}=1$, aplicamos a Regra de Chió:
\begin{equation*}
\det M=
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-3}}&\boldsymbol{\color{blue}{-6}}\\
\boldsymbol{\color{green}{6}}&5&-28\\
\boldsymbol{\color{green}{6}}&3&-53
\end{vmatrix}
\\
\:
\\
\det M=\begin{vmatrix}
5-(-3\cdot 6) & -28-(-6\cdot 6)\\
3-(-3\cdot 6) & -53-(-6\cdot 6)
\end{vmatrix}
\\
\:
\\
\det M=
\begin{vmatrix}
23 & 8\\
21 & -17
\end{vmatrix}
\\
\:
\\
\det M=(23 \cdot (-17))-(21 \cdot 8)=-559
\end{equation*}
O Método de Castilho para resolução de sistemas lineares
Sistemas lineares e determinantes: Origens e desenvolvimento

- Resolvendo O Problema Do Retângulo E Triângulo Inscritos
[veja o problema aqui] Vamos chamar a altura do triângulo de H, conforme a figura abaixo: Note agora que um modo alternativo de enunciar o problema seria este: encontre h que satisfaça a seguinte igualdade:(área do retângulo = área do triângulo)...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Os $10$ Problemas De Apolônio: Problema $1:[ppp]$ Problema Dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares. Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
A Regra de Chió para o cálculo de determinantes
Toda matriz quadrada, de qualquer ordem, tem associada a ela um número chamado determinante da matriz.
Existem alguns métodos para calcular o determinante de uma matriz, como por exemplo a Regra de Sarrus e o Teorema de Laplace utilizando a Matriz de Cofatores.

A Regra de Chió é muito prática se o elemento $a_{11}$ da matriz for igual a $1$, o que nos permite calcular o determinante de uma matriz de ordem $n$ usando uma matriz de ordem $n-1$.
Dada uma matriz quadrada de ordem $n$ sendo $a_{11}=1$:
\begin{equation*}
\begin{bmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
a_{21} & a_{22} & a_{23} & \cdots & a_{2n}\\
a_{31} & a_{32} & a_{33} & \cdots & a_{3n}\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn}
\end{bmatrix}
\end{equation*}
obtemos uma matriz de ordem $n-1$ fazendo:
\begin{equation*}
\begin{bmatrix}
a_{22}-(a_{12}\cdot a_{21}) & a_{23}-(a_{13}\cdot a_{21}) & \cdots & a_{2n}-(a_{1n}\cdot a_{21})\\
a_{32}-(a_{12}\cdot a_{31}) & a_{33}-(a_{13}\cdot a_{31}) & \cdots &a_{3n}-(a_{1n}\cdot a_{31}) \\
\vdots & \vdots & \ddots & \vdots\\
a_{n2}-(a_{12}\cdot a_{n1}) & a_{n3}-(a_{13}\cdot a_{n1}) & \cdots & a_{nn}-(a_{1n}\cdot a_{n1})
\end{bmatrix}
\end{equation*}
Exemplo $1$:
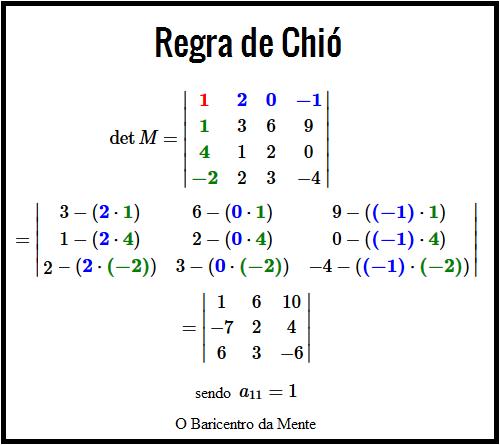
Seja $M$ a matriz quadrada de ordem $4$. Calcular o determinante usando a Regra de Chió.\begin{equation*}
M=
\begin{bmatrix}
1 & 2 & 0 & -1\\
1 & 3 & 6 & 9\\
4 & 1 & 2 & 0\\
-2 & 2 & 3 & -4
\end{bmatrix}
\end{equation*}
Como o elemento $a_{11}=1$, então fazemos:
\begin{equation*}
\det{M}=
\begin{vmatrix}
\boldsymbol {\color{red}{1}} & \boldsymbol{\color{blue}{2}} & \boldsymbol{\color{blue}{0}} & \boldsymbol{\color{blue}{-1}}\\
\boldsymbol{\color{green}{1}} & 3 & 6 & 9\\
\boldsymbol{\color{green}{4}} & 1 & 2 & 0\\
\boldsymbol{\color{green}{-2}} & 2 & 3 & -4
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
3-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{1}}) & 6-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{1}}) & 9-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{1}})\\
1-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{4}})& 2-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{4}}) & 0-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{4}})\\
2-(\boldsymbol {\color{blue}{2}} \cdot \boldsymbol {\color{green}{(-2)}}) & 3-(\boldsymbol {\color{blue}{0}} \cdot \boldsymbol {\color{green}{(-2)}}) & -4-(\boldsymbol {\color{blue}{(-1)}} \cdot \boldsymbol {\color{green}{(-2)}})
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
1 & 6 & 10\\
-7 & 2 & 4\\
6 & 3 & -6
\end{vmatrix}
\end{equation*}
Aqui poderíamos aplicar a Regra de Sarrus, mas vamos aplicar novamente a Regra de Chió, já que o elemento $a_{11}=1$ e assim obteremos um determinante a partir de uma matriz de ordem $2$, resolvido rapidamente.
\begin{equation*}
\det{M}=
\begin{vmatrix}
\boldsymbol {\color{red}{1}} & \boldsymbol{\color{blue}{6}} & \boldsymbol{\color{blue}{10}} \\
\boldsymbol{\color{green}{-7}} & 2 & 4 \\
\boldsymbol{\color{green}{6}} & 3 & -6
\end{vmatrix}
\\
\:
\\
\det{M}=
\begin{vmatrix}
2-(\boldsymbol {\color{blue}{6}} \cdot \boldsymbol {\color{green}{(-7)}}) & 4-(\boldsymbol {\color{blue}{10}} \cdot \boldsymbol {\color{green}{(-7)}}) \\
3-(\boldsymbol {\color{blue}{6}} \cdot \boldsymbol {\color{green}{(6)}}) & -6-(\boldsymbol {\color{blue}{10}} \cdot \boldsymbol {\color{green}{(6)}})
\end{vmatrix}
\\
\:
\
\det{M}=
\begin{vmatrix}
44 & 74\\
-33 & -66
\end{vmatrix}
\\
\:
\\
\det{M}=(44 \cdot (-66)) - (74 \cdot (-33))=-462
\end{equation*}
Assim, o determinante da matriz $M$ é igual a $-462$.
Observações:
$1)$ Se o elemento $a_{11} \neq 1$ e existir algum elemento da matriz que seja igual a $1$, então podemos obter uma matriz equivalente trocando a posição de duas filas (colunas ou linhas).Ao trocarmos de posição duas filas de uma matriz, o determinante da nova matriz é o oposto do determinante da matriz anterior, ou seja, tem o sinal trocado.
Por exemplo: seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
3 & 2 & 0 &-1\\
2 & 3 & 6 &9\\
4 & 1 & 2 &0\\
-2 & 2 & 3 &-1
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}\det{A}=
\begin{vmatrix}
3 & 2 & 0 &-1\\
2 & 3 & 6 &9\\
4 & 1 & 2 &0\\
-2 & 2 & 3 &-1
\end{vmatrix}
\end{equation*}
Trocando a primeira linha pela terceira, obtemos:
\begin{equation*}\det{A}=-
\begin{vmatrix}
4 & 1 & 2 &0\\
2 & 3 & 6 &9\\
3 & 2 & 0 & -1\\
-2 & 2 & 3 &-1
\end{vmatrix}
\end{equation*}
E agora trocamos a primeira coluna pela segunda:
\begin{equation*}\det{A}=
\begin{vmatrix}
1 & 4 & 2 &0\\
3 & 2 & 6 &9\\
2 & 3 & 0 & -1\\
2 & -2 & 3 &-1
\end{vmatrix}
\end{equation*}
Vejam que o sinal do determinante passou de $+$ para $-$ e depois para $+$.
$2)$ Se o elemento $a_{11} \neq 1$ e n]ao houver qualquer elemento da matriz igual a $1$, podemos criar elementos igual a $1$ na matriz usando o Teorema de Jacobi que essencialmente diz que o determinante de uma matriz quadrada não se altera se adicionarmos aos elementos de uma fila qualquer, os elementos correspondentes de outra fila paralela previamente multiplicada por uma constante.
Por exemplo: Seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
3 & 2 & 0 & -1\\
2 & 3 & 6 & 9\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}
\det A=\begin{vmatrix}
3 & 2 & 0 & -1\\
2 & 3 & 6 & 9\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{vmatrix}
\end{equation*}
Como não há um elemento da matriz igual a $1$, vamos criá-lo multiplicando a segunda linha por $-1$ e somá-la à primeira:
\begin{equation*}
\det A=\begin{vmatrix}
3 & 2 & 0 & -1\\
\boldsymbol{\color{red}{2}} & \boldsymbol{\color{red}{3}} & \boldsymbol{\color{red}{6}} & \boldsymbol{\color{red}{9}}\\
4 & 5 & 2 & 0\\
-2 & 2 & 3 & -4
\end{vmatrix}
\begin{matrix}
\longleftarrow & + & \looparrowleft \\
\longrightarrow & \times &(-1) \\
~\\
~\\
\end{matrix}
=
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{-6}}&\boldsymbol{\color{blue}{-10}}\\
2&3&6&9\\
4&5&2&0\\
-2&2&3&-4
\end{vmatrix}
\end{equation*}
Ao calcularmos o determinante da matriz equivalente, veremos que é igual ao determinante da matriz original.
$3)$ Se o elemento $a_{11} \neq 1$ e não houver outro elemento igual a $1$ na matriz, podemos criar elementos igual a $1$ na matriz colocando um fator $k$ comum a uma fila em evidência, pois se todos os elementos de uma fila de uma matriz quadrada são multiplicados por um mesmo número $k$, então seu determinante fica multiplicado por $k$.
Por exemplo: Seja a matriz:
\begin{equation*}
A=
\begin{bmatrix}
2&4&-2\\
10&6&0\\
4&-4&10
\end{bmatrix}
\end{equation*}
O determinante da matriz $A$ será dado por:
\begin{equation*}
\det A=
\begin{vmatrix}
\boldsymbol{\color{red}{2}}&\boldsymbol{\color{red}{4}}&\boldsymbol{\color{red}{-2}}\\
10&6&0\\
4&-4&10
\end{vmatrix}
=
2
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&\boldsymbol{\color{blue}{2}}&\boldsymbol{\color{blue}{-1}}\\
10&6&0\\
4&-4&10
\end{vmatrix}
\end{equation*}
Exemplo $2$:
Encontrar o determinante da matriz quadrada de ordem $5$ abaixo:\begin{equation*}
M=
\begin{bmatrix}
2&-1&0&3&2\\
-2&3&2&0&-2\\
-3&2&-1&-5&4\\
-1&3&2&-2&0\\
0&4&-2&-1&3
\end{bmatrix}
\end{equation*}
Nesta matriz, o elemento $a_{11}\neq 1$ e não há nenhum outro elemento da matriz que seja igual a $1$. Para que o elemento $a_{11}$ seja igual a $1$, multiplicamos a segunda coluna por $1$ e somamos o resultado com a primeira coluna:
\begin{equation*}
\det M=
\begin{vmatrix}
2&\boldsymbol{\color{red}{-1}}&0&3&2\\
-2&\boldsymbol{\color{red}{3}}&2&0&-2\\
-3&\boldsymbol{\color{red}{2}}&-1&-5&4\\
-1&\boldsymbol{\color{red}{3}}&2&-2&0\\
0&\boldsymbol{\color{red}{4}}&-2&-1&3
\end{vmatrix}
=
\begin{vmatrix}
\boldsymbol{\color{blue}{1}}&-1&0&3&2\\
\boldsymbol{\color{blue}{1}}&3&2&0&-2\\
\boldsymbol{\color{blue}{-1}}&2&-1&-5&4\\
\boldsymbol{\color{blue}{2}}&3&2&-2&0\\
\boldsymbol{\color{blue}{4}}&4&-2&-1&3
\end{vmatrix}
\end{equation*}
Agora, podemos aplicar a Regra de Chió:
\begin{equation*}
\det M=
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{0}}&\boldsymbol{\color{blue}{3}}&\boldsymbol{\color{blue}{2}}\\
\boldsymbol{\color{green}{1}}&3&2&0&-2\\
\boldsymbol{\color{green}{-1}}&2&-1&-5&4\\
\boldsymbol{\color{green}{2}}&3&2&-2&0\\
\boldsymbol{\color{green}{4}}&4&-2&-1&3
\end{vmatrix}
\\
\:
\\
=
\begin{vmatrix}
3-(\color{blue}{-1}\cdot \color{green}{1}) & 2-(\color{blue}{0}\cdot \color{green}{1}) & 0-(\color{blue}{3}\cdot \color{green}{1}) & -2-(\color{blue}{2}\cdot \color{green}{1})\\
2-(\color{blue}{-1}\cdot \color{green}{(-1)}) & -1-(\color{blue}{0}\cdot \color{green}{(-1)}) & -5-(\color{blue}{3}\cdot \color{green}{(-1)}) & 4-(\color{blue}{2}\cdot \color{green}{(-1)})\\
3-(\color{blue}{-1}\cdot \color{green}{2}) & 2-(\color{blue}{0}\cdot \color{green}{2}) & -2-(\color{blue}{3}\cdot \color{green}{2}) &0-(\color{blue}{2}\cdot \color{green}{2})\\
4-(\color{blue}{-1}\cdot \color{green}{4}) & -2-(\color{blue}{0}\cdot \color{green}{4}) & -1-(\color{blue}{3}\cdot \color{green}{4}) & 3-(\color{blue}{2}\cdot \color{green}{4})
\end{vmatrix}
\\
\:
\\
=
\begin{vmatrix}
4&2&-3&-4\\
1&-1&-2&6\\
5&2&-8&-4\\
8&-2&-13&-5
\end{vmatrix}
\end{equation*}
Agora, trocamos a segunda linha pela primeira e aplicamos a Regra de Chió novamente. Como estaremos trocando apenas um linha, não podemos nos esquecer de trocar o sinal do determinante:
\begin{equation*}
\det M=-
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-1}}&\boldsymbol{\color{blue}{-2}}&\boldsymbol{\color{blue}{6}}\\
\boldsymbol{\color{green}{4}}&2&-3&-4\\
\boldsymbol{\color{green}{5}}&2&-8&-4\\
\boldsymbol{\color{green}{8}}&-2&-13&-5
\end{vmatrix}
\\
\:
\\
=-
\begin{vmatrix}
2-(-1\cdot 4) & -3-(-2\cdot 4) & -4-(6\cdot 4)\\
2-(-1 \cdot 5) & -8-(-2 \cdot 5) & -4-(6 \cdot 5)\\
-2-(-1\cdot 8) & -13-(-2\cdot8) & -5-(6\cdot8)
\end{vmatrix}
\\
\:
\\
=-
\begin{vmatrix}
6&5&-28\\
7&2&-34\\
6&3&-53
\end{vmatrix}
\end{equation*}
Aqui, podemos aplicar a Regra de Sarrus ou ainda aplica a Regra de Chió novamente. Primeiramente trocamos a segunda linha pela primeira, já trocando o sinal do determinante:
\begin{equation*}
\det M=
\begin{vmatrix}
7&2&-34\\
6&5&-28\\
6&3&-53
\end{vmatrix}
\end{equation*}
Agora, multiplicamos a segunda linha por $-1$ e somamos o resultado à primeira linha:
\begin{equation*}
\det M=
\begin{vmatrix}
1&-3&-6\\
6&5&-28\\
6&3&-53
\end{vmatrix}
\end{equation*}
Agora que o elemento $a_{11}=1$, aplicamos a Regra de Chió:
\begin{equation*}
\det M=
\begin{vmatrix}
\boldsymbol{\color{red}{1}}&\boldsymbol{\color{blue}{-3}}&\boldsymbol{\color{blue}{-6}}\\
\boldsymbol{\color{green}{6}}&5&-28\\
\boldsymbol{\color{green}{6}}&3&-53
\end{vmatrix}
\\
\:
\\
\det M=\begin{vmatrix}
5-(-3\cdot 6) & -28-(-6\cdot 6)\\
3-(-3\cdot 6) & -53-(-6\cdot 6)
\end{vmatrix}
\\
\:
\\
\det M=
\begin{vmatrix}
23 & 8\\
21 & -17
\end{vmatrix}
\\
\:
\\
\det M=(23 \cdot (-17))-(21 \cdot 8)=-559
\end{equation*}
Referências:
[1] Matemática, Contexto & Aplicações V2 - Dante - Editora ÁticaVeja mais:
Matrizes e o controle de tráfegoO Método de Castilho para resolução de sistemas lineares
Sistemas lineares e determinantes: Origens e desenvolvimento

- Resolvendo O Problema Do Retângulo E Triângulo Inscritos
[veja o problema aqui] Vamos chamar a altura do triângulo de H, conforme a figura abaixo: Note agora que um modo alternativo de enunciar o problema seria este: encontre h que satisfaça a seguinte igualdade:(área do retângulo = área do triângulo)...
- A Desigualdade De Ptolomeu
Cláudio Ptolomeu foi um grande astrônomo e geômetra grego que viveu no século $I\ \text{d.C.}$. Neste post, provaremos uma desigualdade geométrica muito interessante. Proposição 1Dado o quadrilátero $ABCD$, onde $AC$ e $BD$ são as diagonais,...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Os $10$ Problemas De Apolônio: Problema $1:[ppp]$ Problema Dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares. Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
