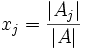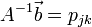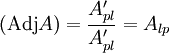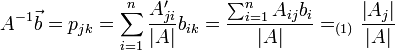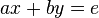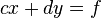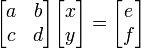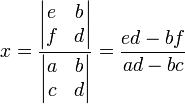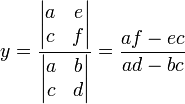Matemática

Sejam:
Usando as propriedades da multiplicação de matrizes:
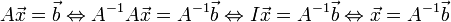
então:
- Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Representação Matricial De Um Sistema
Um sistema de equações pode ser representado na forma de uma matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. O sistema terá a seguinte...
- Solução De Um Sistema Utilizando A Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Sistemas Pela Regra De Cramer
Um sistema de duas equações com duas incógnitas pode ser resolvido pelos seguintes métodos: adição e subtração. Os sistemas que apresentam três ou mais equações envolvendo três ou mais incógnitas também podem ser resolvidos pelos métodos...
- Regra De Cramer Para Resolução De Sistemas
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso email [email protected] HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com...
Matemática
Regra de Cramer

A Regra de Cramer é um teorema em álgebra linear, que dá a solução de um sistema de equações lineares em termos de determinantes. Recebe este nome em homenagem a Gabriel Cramer (1704 - 1752).
Se 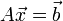 é um sistema de equações. (A é a matriz de coeficientes do sistema,
é um sistema de equações. (A é a matriz de coeficientes do sistema, 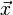 é o vetor coluna das incógnitas e
é o vetor coluna das incógnitas e 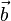 é o vetor coluna os termos independentes)
é o vetor coluna os termos independentes)
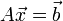 é um sistema de equações. (A é a matriz de coeficientes do sistema,
é um sistema de equações. (A é a matriz de coeficientes do sistema, 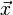 é o vetor coluna das incógnitas e
é o vetor coluna das incógnitas e 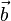 é o vetor coluna os termos independentes)
é o vetor coluna os termos independentes) Então a solução ao sistema se apresenta assim:
Em que Aj é a matriz que se obtém da matriz A substituindo a coluna j pela coluna dos termos independentes b.
DEMONSTRAÇÃO
Usando as propriedades da multiplicação de matrizes:
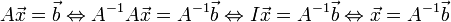
então:
Recordando a definição de determinante, o somatório definido acumula a multiplicação do elemento adjunto o cofator da posição ij, com o elemento i-ésimo do vetor B (que é precisamente o elemento i-ésimo da coluna j, na matriz Aj
EXEMPLO:
Um bom exemplo é a resolução de um simples sistema de equações 2x2:
Dado
REFERÊNCIAS
http://pt.wikipedia.org/wiki/Regra_de_Cramer
- Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Representação Matricial De Um Sistema
Um sistema de equações pode ser representado na forma de uma matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. O sistema terá a seguinte...
- Solução De Um Sistema Utilizando A Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Sistemas Pela Regra De Cramer
Um sistema de duas equações com duas incógnitas pode ser resolvido pelos seguintes métodos: adição e subtração. Os sistemas que apresentam três ou mais equações envolvendo três ou mais incógnitas também podem ser resolvidos pelos métodos...
- Regra De Cramer Para Resolução De Sistemas
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso email [email protected] HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com...