Matemática
Nesta postagem, vamos provar que:
\begin{equation*}
\int \frac{x \pm 1}{x \mp 1}\ dx = x \pm \ln |x \mp 1 |+C
\end{equation*}
onde $x \in \mathbb{R}$ tal que $x \neq \pm 1$.
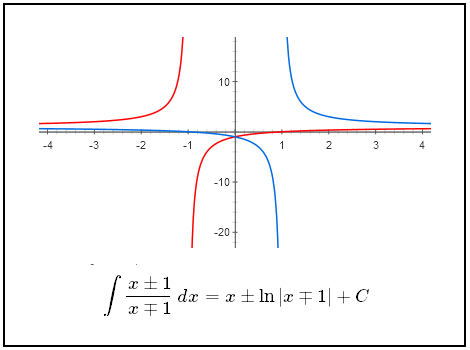
Vamos separar o integrando em duas funções distintas e mostrar o processo de integração de cada uma delas separadamente e no fim, podemos unir os resultados. Temos então que:
\begin{equation*}
f(x) = \frac{x+1}{x-1} \qquad \text{e} \qquad g(x)=\frac{x-1}{x+1}
\end{equation*}
Seja a integral:
\begin{equation*}
I = \int \frac{x+1}{x-1}\ dx
\end{equation*}
Para o integrando, expandimos a divisão como:
\begin{equation*}
I = \int \left( \frac{2}{x-1}+1\right)\ dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \int \frac{2}{x-1}\ dx + \int dx \\
\ \\
I = 2 \int \frac{1}{x-1}\ dx + \int dx
\end{equation*}
Para o integrando $\displaystyle \frac{1}{x-1}$, fazemos a substituição $u=x-1$ e $du=dx$:
\begin{equation*}
I = 2\int \frac{1}{u}\ du + x
\end{equation*}
A integral de $1/u$ é $\ln(u)$:
\begin{equation*}
I = 2\ln(u) + x + C
\end{equation*}
Mas $u=x-1$, logo:
\begin{equation*}
I = x+2\ln |x-1|+C
\end{equation*}
Seja a integral:
\begin{equation*}
I = \int \frac{x-1}{x+1}\ dx
\end{equation*}
Para o integrando, expandimos a divisão como:
\begin{equation*}
I = \int \left(1 - \frac{2}{x+1}\right)\ dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \int dx -2\int \frac{1}{x+1}\ dx
\end{equation*}Para o integrando $\displaystyle \frac{1}{x+1}$, fazemos a substituição $u=x+1$ e $du=dx$:
\begin{equation*}
I = x - 2\int \frac{1}{u}\ du
\end{equation*}
A integral de $1/u$ é $\ln(u)$:
\begin{equation*}
I = x - 2\ln(u) + C
\end{equation*}
Mas $u=x+1$, logo:
\begin{equation*}
I = x-2\ln |x+1|+C
\end{equation*}
Analisando os dois resultados obtidos, podemos escrever:
\begin{equation*}
\int \frac{x \pm 1}{x \mp 1}\ dx = x \pm 2 \ln|x\mp 1|+C
\end{equation*}
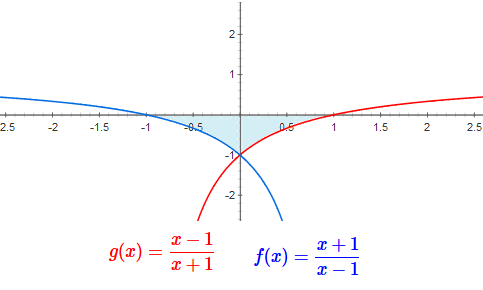
Para sabermos os limites de integração, primeiramente devemos analisar as curvas para determinarmos em quais pontos elas cortam os eixos dos $x$ e dos $y$.
O ponto em que a curva corta o eixo dos $x$ é a raiz da função e para determinarmos esse ponto, basta igualarmos a função a zero, ou seja, fazemos $y=0$. Assim:
\begin{equation*}
f(x)=\frac{x+1}{x-1}\ \Longrightarrow \ 0=\frac{x+1}{x-1}\ \Longrightarrow x=-1
\end{equation*}
e
\begin{equation*}
g(x)=\frac{x-1}{x+1}\ \Longrightarrow \ 0=\frac{x-1}{x+1}\ \Longrightarrow x=1
\end{equation*}
Estas são as raízes. Para sabermos o ponto em que as curvas cortam o eixo dos $y$, basta fazermos $x=0$:
\begin{equation*}
f(x) = \frac{1}{-1}\ \Longrightarrow \ y=-1
\end{equation*}
e
\begin{equation*}
g(x)=\frac{-1}{1}\ \Longrightarrow \ y=-1
\end{equation*}
As duas funções cortam o eixo dos $y$ no ponto $y=-1$.
A área procurada é dada pela soma das áreas sobre as curvas $f(x)$ no intervalo $[-1,0]$ e $g(x)$ no intervalo $[0,1]$. Desta forma, vamos calcular cada uma das áreas separadamente e somá-las para obter a área total.
Vamos calcular primeiro a área sobre a curva $f(x)$:
\begin{equation*}
A_{f(x)} = \int _{-1}^{0} \frac{x+1}{x-1}\ dx\\
\ \\
A_{f(x)} =\left[ x+2\ln |x-1| \right]_{-1}^0\\
\ \\
A_{f(x)} =2\ln (-1)-2\ln (-2)+1\\
\ \\
A_{f(x)} =2\ln \left( \frac{1}{2} \right)+ 1\\
\ \\
A_{f(x)} =\ln \left(\frac{1}{4}\right)+1\\
\ \\
A_{f(x)} \approx -0,38629
\end{equation*}
Agora, vamos calcular a área sobre a curva $g(x)$:
\begin{equation*}
A_{g(x)} = \int _{0}^{1} \frac{x-1}{x+1}\ dx\\
\ \\
A_{g(x)} =\left[ x-2\ln |x+1| \right]_0^1\\
\ \\
A_{g(x)} =1 - 2\ln (2)-2\ln (1)\\
\ \\
A_{g(x)} =1+2\ln \left( \frac{1}{2} \right)\\
\ \\
A_{g(x)} =1+\ln(2^{-1}) \\
\ \\
A_{g(x)} = 1-\ln(2)\\
\ \\
A_{g(x)} \approx -0,38629
\end{equation*}
A área total é dada pela soma:
\begin{equation*}
A = A_{f(x)}+A_{g(x)}\\
A= -0,38629-0,39629\\
A=-0,772588
\end{equation*}
Não existe área negativa. Este sinal de negativo que encontramos após a integração, quer dizer apenas que a área encontrada localiza-se abaixo do eixo dos $x$. Assim, a área procurada é:
\begin{equation*}
A=0,772588\ u.a.
\end{equation*}
Integração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{1}{ax+b}\ Dx$
Nesta postagem vermos que: \begin{equation*} \int \frac{1}{ax+b}\ dx = \frac{1}{a}\ln |ax+b| + C \end{equation*} onde $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq 0$. [Família de funções integráveis do tipo $\displaystyle \frac{1}{ax+b}$] Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
Matemática
Resolução da integral $\displaystyle \int \frac{x \pm 1}{x \mp 1}\ dx$
Nesta postagem, vamos provar que:
\begin{equation*}
\int \frac{x \pm 1}{x \mp 1}\ dx = x \pm \ln |x \mp 1 |+C
\end{equation*}
onde $x \in \mathbb{R}$ tal que $x \neq \pm 1$.
Vamos separar o integrando em duas funções distintas e mostrar o processo de integração de cada uma delas separadamente e no fim, podemos unir os resultados. Temos então que:
\begin{equation*}
f(x) = \frac{x+1}{x-1} \qquad \text{e} \qquad g(x)=\frac{x-1}{x+1}
\end{equation*}
Resolução da integral de $f(x)$
Seja a integral:
\begin{equation*}
I = \int \frac{x+1}{x-1}\ dx
\end{equation*}
Para o integrando, expandimos a divisão como:
\begin{equation*}
I = \int \left( \frac{2}{x-1}+1\right)\ dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \int \frac{2}{x-1}\ dx + \int dx \\
\ \\
I = 2 \int \frac{1}{x-1}\ dx + \int dx
\end{equation*}
Para o integrando $\displaystyle \frac{1}{x-1}$, fazemos a substituição $u=x-1$ e $du=dx$:
\begin{equation*}
I = 2\int \frac{1}{u}\ du + x
\end{equation*}
A integral de $1/u$ é $\ln(u)$:
\begin{equation*}
I = 2\ln(u) + x + C
\end{equation*}
Mas $u=x-1$, logo:
\begin{equation*}
I = x+2\ln |x-1|+C
\end{equation*}
Resolução da integral de $g(x)$
Seja a integral:
\begin{equation*}
I = \int \frac{x-1}{x+1}\ dx
\end{equation*}
Para o integrando, expandimos a divisão como:
\begin{equation*}
I = \int \left(1 - \frac{2}{x+1}\right)\ dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \int dx -2\int \frac{1}{x+1}\ dx
\end{equation*}Para o integrando $\displaystyle \frac{1}{x+1}$, fazemos a substituição $u=x+1$ e $du=dx$:
\begin{equation*}
I = x - 2\int \frac{1}{u}\ du
\end{equation*}
A integral de $1/u$ é $\ln(u)$:
\begin{equation*}
I = x - 2\ln(u) + C
\end{equation*}
Mas $u=x+1$, logo:
\begin{equation*}
I = x-2\ln |x+1|+C
\end{equation*}
Analisando os dois resultados obtidos, podemos escrever:
\begin{equation*}
\int \frac{x \pm 1}{x \mp 1}\ dx = x \pm 2 \ln|x\mp 1|+C
\end{equation*}
Exemplo
Calcular a área hachurada entre as curvas $\displaystyle f(x)=\frac{x+1}{x-1}$ e $\displaystyle g(x)=\frac{x-1}{x+1}$.
Para sabermos os limites de integração, primeiramente devemos analisar as curvas para determinarmos em quais pontos elas cortam os eixos dos $x$ e dos $y$.
O ponto em que a curva corta o eixo dos $x$ é a raiz da função e para determinarmos esse ponto, basta igualarmos a função a zero, ou seja, fazemos $y=0$. Assim:
\begin{equation*}
f(x)=\frac{x+1}{x-1}\ \Longrightarrow \ 0=\frac{x+1}{x-1}\ \Longrightarrow x=-1
\end{equation*}
e
\begin{equation*}
g(x)=\frac{x-1}{x+1}\ \Longrightarrow \ 0=\frac{x-1}{x+1}\ \Longrightarrow x=1
\end{equation*}
Estas são as raízes. Para sabermos o ponto em que as curvas cortam o eixo dos $y$, basta fazermos $x=0$:
\begin{equation*}
f(x) = \frac{1}{-1}\ \Longrightarrow \ y=-1
\end{equation*}
e
\begin{equation*}
g(x)=\frac{-1}{1}\ \Longrightarrow \ y=-1
\end{equation*}
As duas funções cortam o eixo dos $y$ no ponto $y=-1$.
A área procurada é dada pela soma das áreas sobre as curvas $f(x)$ no intervalo $[-1,0]$ e $g(x)$ no intervalo $[0,1]$. Desta forma, vamos calcular cada uma das áreas separadamente e somá-las para obter a área total.
Vamos calcular primeiro a área sobre a curva $f(x)$:
\begin{equation*}
A_{f(x)} = \int _{-1}^{0} \frac{x+1}{x-1}\ dx\\
\ \\
A_{f(x)} =\left[ x+2\ln |x-1| \right]_{-1}^0\\
\ \\
A_{f(x)} =2\ln (-1)-2\ln (-2)+1\\
\ \\
A_{f(x)} =2\ln \left( \frac{1}{2} \right)+ 1\\
\ \\
A_{f(x)} =\ln \left(\frac{1}{4}\right)+1\\
\ \\
A_{f(x)} \approx -0,38629
\end{equation*}
Agora, vamos calcular a área sobre a curva $g(x)$:
\begin{equation*}
A_{g(x)} = \int _{0}^{1} \frac{x-1}{x+1}\ dx\\
\ \\
A_{g(x)} =\left[ x-2\ln |x+1| \right]_0^1\\
\ \\
A_{g(x)} =1 - 2\ln (2)-2\ln (1)\\
\ \\
A_{g(x)} =1+2\ln \left( \frac{1}{2} \right)\\
\ \\
A_{g(x)} =1+\ln(2^{-1}) \\
\ \\
A_{g(x)} = 1-\ln(2)\\
\ \\
A_{g(x)} \approx -0,38629
\end{equation*}
A área total é dada pela soma:
\begin{equation*}
A = A_{f(x)}+A_{g(x)}\\
A= -0,38629-0,39629\\
A=-0,772588
\end{equation*}
Não existe área negativa. Este sinal de negativo que encontramos após a integração, quer dizer apenas que a área encontrada localiza-se abaixo do eixo dos $x$. Assim, a área procurada é:
\begin{equation*}
A=0,772588\ u.a.
\end{equation*}
Veja mais:
Lista de resolução de integraisIntegração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{1}{ax+b}\ Dx$
Nesta postagem vermos que: \begin{equation*} \int \frac{1}{ax+b}\ dx = \frac{1}{a}\ln |ax+b| + C \end{equation*} onde $a$ e $b$ $\in \mathbb{R}$, sendo $a \neq 0$. [Família de funções integráveis do tipo $\displaystyle \frac{1}{ax+b}$] Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
