Matemática
Seja a integral:
\begin{equation}
\int \frac{1}{(x^2-1)^2}dx=I
\end{equation}
I = \int \frac{1}{(x^2-1)(x^2-1)}dx = \int \frac{1}{(x+1)(x-1)(x+1)(x-1)}dx
\end{equation}
\frac{1}{(x+1)^2(x-1)^2}=\frac{A}{(x+1)}+\frac{B}{(x+1)^2}+\frac{C}{(x-1)}+\frac{D}{(x-1)^2}
\end{equation}
Eliminando o denominador, obtemos:
\begin{equation*}
1=A(x+1)(x-1)^2+B(x-1)^2+C(x-1)(x+1)^2+D(x+1)^2
\end{equation*}
Aplicando a distributiva:
\begin{equation*}
1=Ax^3-Ax^2-Ax+A+Bx^2-2Bx+B+Cx^3+Cx^2-Cx-C+Dx^2+2Dx+D
\end{equation*}
Fatorando as potências:
\begin{equation*}
1=x^3(A+C)+x^2(-A+B+C+D)+x(-A-2B-C+2D+A+B-C+D
\end{equation*}
\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
-A & -2B & -C &+2D &=0 \\
A & +B & -C & +D &=1\\
A & & +C & &=0
\end{matrix}\right.
\end{equation}
\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& -3B & -2C & +D &=0 \\
& +2B & & +2D &=1\\
& B & +2C & D&=0
\end{matrix}\right.
\end{equation}
\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& B & +2C & D&=0\\
& -3B & -2C & +D &=0 \\
& +2B & & +2D &=1\\
\end{matrix}\right.
\end{equation}
\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& B & +2C & D&=0\\
& & 4C & +4D &=0 \\
& & -4C & &=1\\
\end{matrix}\right.
\end{equation}
I=\int \left( \frac{1}{4(x+1)}+\frac{1}{4(x+1)^2}-\frac{1}{4(x-1)}+\frac{1}{4(x-1)^2}\right) dx
\end{equation}
Integrando termo a termo:
\begin{equation}
I=\frac{1}{4}\int\frac{dx}{(x+1)}+\frac{1}{4}\int \frac{dx}{(x+1)^2}-\frac{1}{4}\int \frac{dx}{(x-1)}+\frac{1}{4}\int \frac{dx}{(x-1)^2}
\end{equation}
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x+1)}$, fazemos $u=x+1$ e $du=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x+1)^2}$, fazemos $v=x+1$ e $dv=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x-1)}$, fazemos $p=x-1$ e $dp=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x-1)^2}$, fazemos $w=x-1$ e $dw=dx$.
Substituindo em cada integral de $(9)$, obtemos:
\begin{equation}
\begin{matrix}
I=\frac{1}{4}\int \frac{du}{u}+\frac{1}{4}\int \frac{dv}{v^2}-\frac{1}{4}\int \frac{dp}{p}+\frac{1}{4}\int \frac{dw}{x^2}\\
I=\frac{1}{4}\ln (u)-\frac{1}{4v}-\frac{1}{4}\ln(p) - \frac{1}{4w}+C\\
I=\frac{1}{4}\left[\ln(u)-\ln(p)-\frac{1}{v}-\frac{1}{w}\right]+C
\end{matrix}
\end{equation}
Substituindo $u$, $v$, $p$ e $w$:
\begin{equation}
\begin{matrix}
I=\frac{1}{4}\left[\ln(x+1)-\ln(x-1)-\frac{1}{x+1}-\frac{1}{x-1}\right]+C\\
I=\frac{1}{4}\left[\ln(x+1)-\ln(x-1)-\frac{(x-1)-(x+1)}{(x^2-1)}\right]+C\\
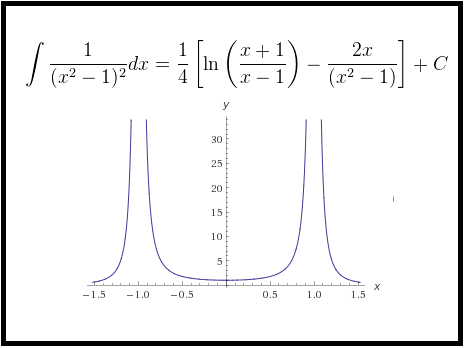
I=\frac{1}{4}\left[\ln \left(\frac{x+1}{x-1}\right)-\frac{2x}{(x^2-1)}\right]+C
\end{matrix}
\end{equation}
Integral por Frações Parciais - Fatores Lineares
Integral por Frações Parciais - Fatores Quadráticos

- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Resolução da Integral $\int \frac{1}{(x^2-1)^2}dx$
Integrais por frações parciais às vezes podem ser complicadas de serem resolvidas. Às vezes é mais complicado encontrar as frações parciais equivalente ao integrando do que resolver as integrais obtidas após este processo. Este é um exemplo interessante porque além de trabalharmos com métodos de integração, utilizamos o método de eliminação de Gauss na resolução do sistema linear que geram as frações parciais. Veremos passo a passo cada etapa desta resolução.

Seja a integral:
\begin{equation}
\int \frac{1}{(x^2-1)^2}dx=I
\end{equation}
Sugiro a leitura do artigo sobre o método de integração por frações parciais. Primeiramente, fatoramos o denominador do integrando:
\begin{equation}I = \int \frac{1}{(x^2-1)(x^2-1)}dx = \int \frac{1}{(x+1)(x-1)(x+1)(x-1)}dx
\end{equation}
Como há fatores lineares no denominador e eles se repetem, este é o segundo caso do método para denominadores lineares. Vejam o o artigo aqui. O integrando deve ser:
\begin{equation}\frac{1}{(x+1)^2(x-1)^2}=\frac{A}{(x+1)}+\frac{B}{(x+1)^2}+\frac{C}{(x-1)}+\frac{D}{(x-1)^2}
\end{equation}
Eliminando o denominador, obtemos:
\begin{equation*}
1=A(x+1)(x-1)^2+B(x-1)^2+C(x-1)(x+1)^2+D(x+1)^2
\end{equation*}
Aplicando a distributiva:
\begin{equation*}
1=Ax^3-Ax^2-Ax+A+Bx^2-2Bx+B+Cx^3+Cx^2-Cx-C+Dx^2+2Dx+D
\end{equation*}
Fatorando as potências:
\begin{equation*}
1=x^3(A+C)+x^2(-A+B+C+D)+x(-A-2B-C+2D+A+B-C+D
\end{equation*}
Agora, igualamos os coeficientes dos dois membros da relação, obtendo o sistema linear:
\begin{equation}\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
-A & -2B & -C &+2D &=0 \\
A & +B & -C & +D &=1\\
A & & +C & &=0
\end{matrix}\right.
\end{equation}
Para resolver este sistema, utilizaremos o Método de Eliminação de Gauss (escalonamento), deixando o sistema triangular superior. Para eliminar o termo que contém $A$ da segunda equação, somamo-a à primeira equação multiplicada por $-1$; Para eliminar o termo que contém $A$ da terceira equação, basta somarmos com a primeira equação; E o mesmo ocorre com a quarta equação. Então obtemos:
\begin{equation} \left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& -3B & -2C & +D &=0 \\
& +2B & & +2D &=1\\
& B & +2C & D&=0
\end{matrix}\right.
\end{equation}
Para facilitar o escalonamento, utilizaremos as propriedades, trocando a quarta pela segunda equação, e a segunda pela terceira equação:
\begin{equation}\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& B & +2C & D&=0\\
& -3B & -2C & +D &=0 \\
& +2B & & +2D &=1\\
\end{matrix}\right.
\end{equation}
Para eliminarmos o termo que contém $B$ da terceira e quarta equações, somamos a terceira equação com a segunda multiplicada por $3$; e somamos a quarta equação com a segunda multiplicada por $-2$. Obtemos:
\begin{equation}\left\{\begin{matrix}
-A & +B & +C & +D &=0\\
& B & +2C & D&=0\\
& & 4C & +4D &=0 \\
& & -4C & &=1\\
\end{matrix}\right.
\end{equation}
Temos imediatamente que $C=-1/4$. Substituindo $C$ na terceira equação, obtemos $D=1/4$. Substituindo $C$ e $D$ na segunda equação, obtemos $B=1/4$. Finalmente, substituindo $B$, $C$ e $D$ na primeira equação, obtemos $A=1/4$. Agora já temos condições de substituir estes valores nas frações parciais :
\begin{equation}I=\int \left( \frac{1}{4(x+1)}+\frac{1}{4(x+1)^2}-\frac{1}{4(x-1)}+\frac{1}{4(x-1)^2}\right) dx
\end{equation}
Integrando termo a termo:
\begin{equation}
I=\frac{1}{4}\int\frac{dx}{(x+1)}+\frac{1}{4}\int \frac{dx}{(x+1)^2}-\frac{1}{4}\int \frac{dx}{(x-1)}+\frac{1}{4}\int \frac{dx}{(x-1)^2}
\end{equation}
Para resolvermos cada uma das quatro integrais acima, utilizaremos o Método da Substituição. Fazemos:
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x+1)}$, fazemos $u=x+1$ e $du=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x+1)^2}$, fazemos $v=x+1$ e $dv=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x-1)}$, fazemos $p=x-1$ e $dp=dx$;
$\bullet$ Para o integrando $\displaystyle \frac{1}{(x-1)^2}$, fazemos $w=x-1$ e $dw=dx$.
Substituindo em cada integral de $(9)$, obtemos:
\begin{equation}
\begin{matrix}
I=\frac{1}{4}\int \frac{du}{u}+\frac{1}{4}\int \frac{dv}{v^2}-\frac{1}{4}\int \frac{dp}{p}+\frac{1}{4}\int \frac{dw}{x^2}\\
I=\frac{1}{4}\ln (u)-\frac{1}{4v}-\frac{1}{4}\ln(p) - \frac{1}{4w}+C\\
I=\frac{1}{4}\left[\ln(u)-\ln(p)-\frac{1}{v}-\frac{1}{w}\right]+C
\end{matrix}
\end{equation}
Substituindo $u$, $v$, $p$ e $w$:
\begin{equation}
\begin{matrix}
I=\frac{1}{4}\left[\ln(x+1)-\ln(x-1)-\frac{1}{x+1}-\frac{1}{x-1}\right]+C\\
I=\frac{1}{4}\left[\ln(x+1)-\ln(x-1)-\frac{(x-1)-(x+1)}{(x^2-1)}\right]+C\\
I=\frac{1}{4}\left[\ln \left(\frac{x+1}{x-1}\right)-\frac{2x}{(x^2-1)}\right]+C
\end{matrix}
\end{equation}
Veja mais
Integral por SubstituiçãoIntegral por Frações Parciais - Fatores Lineares
Integral por Frações Parciais - Fatores Quadráticos

- Resolução Da Integral $\int \frac{1}{a\ E^{bx}}dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{a\ e^{bx}}dx = -\frac{e^{-bx}}{ab}+C \end{equation*} onde $a$ e $b \in \mathbb{R}$ e $a$ e $b \neq 0$. Seja a integral: \begin{equation*} I = \int \frac{1}{a\ e^{bx}}dx = \int \frac{e^{-bx}}{a}...
- Integral Indefinida Do Produto De Cossenos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois cossenos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation} \int \cos(ax) \cos(bx)dx = \frac{\text{sen}[(a-b)x]}{2(a-b)} + \frac{\text{sen}[(a+b)x]}{2(a+b)}...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
