Matemática
Identificando dois triângulos semelhantes
Exemplo:
Verifique se os triângulos a seguir são proporcionais.
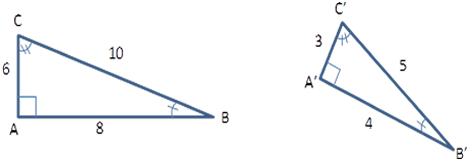
Ao verificarmos a congruência dos ângulos, teremos que:

Temos agora que verificar a proporcionalidade dos lados.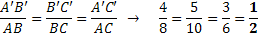
Note que todos os lados possuem a mesma razão de proporcionalidade (1/2).
Sendo assim, podemos afirmar que
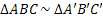
- Questão 36 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Seguem três afirmações sobre semelhança de polígonos: I. se os lados de dois triângulos são respectivamente paralelos dois a dois, então esses triângulos são semelhantes; II. todos os losangos que têm as medidas das duas diagonais iguais entre...
- Questão 80 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Observe as sentenças a seguir. I. Triângulos retângulos cujas hipotenusas medem a ? 2 unidades, sendo a um número real positivo, são semelhantes.II. Triângulos com todos os ângulos internos medindo 60º, são semelhantes.III. Triângulos com lados...
- Semelhança De Polígonos
Polígonos são regiões planas fechadas, constituídas de lados, vértices e ângulos. Dizemos que dois polígonos são semelhantes quando eles possuem o mesmo número de lados e se adéquam às seguintes condições: Ângulos iguais. Lados correspondentes...
- SemelhanÇa
Conceito: Duas figuras são semelhantes se tiverem a mesma forma (não importa o tamanho). EXEMPLOS Dizdemos que: -- Duas circunferências são sempre semelhantes.-- Dois quadrados são sempre semelhantes. TRIÂNGULO SEMELHANTES Observe...
- Semelhança
SEMELHANÇA Conceito: Duas figuras são semelhantes se tiverem a mesma forma (não importa o tamanho). EXEMPLOS Dizdemos que: -- Duas circunferências são sempre semelhantes.-- Dois quadrados são sempre semelhantes. TRIÂNGULO SEMELHANTES...
Matemática
Semelhança de Triângulos

Identificando dois triângulos semelhantes
Sabemos que triângulos são polígonos. Sendo assim, o estudo que é feito para identificar a semelhança defiguras poligonais será válido para o estudo da semelhança de triângulos. Com isso, dois triângulos serão semelhantes se satisfizerem duas condições simultaneamente: se seus lados correspondentes possuírem medidas proporcionais e se os ângulos correspondentes forem iguais (congruentes).
Se invertermos a afirmação feita acima, teremos um fato verdadeiro: as condições são satisfeitas somente quando os triângulos são semelhantes.
Vejamos um desenho para que possamos compreender melhor:
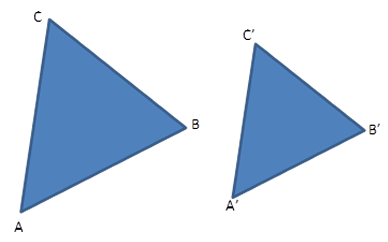
Antes, temos que determinar a correspondência dos vértices de cada triângulo, pois assim determinaremos a correspondência dos lados e dos ângulos entre estes dois triângulos.
Os vértices A, B, C correspondem, respectivamente, aos vértices A’, B’, C’. Sendo assim, montaremos as razões de proporcionalidade entre os lados correspondentes.
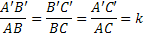
Uma das condições é que todos os lados correspondentes possuam uma proporcionalidade, que chamaremos neste caso de k. Ressaltando que essa razão foi construída pela divisão de cada lado correspondente: veja que o lado A’B’ do segundo triângulo corresponde ao lado AB do primeiro triângulo. Por este fato, a divisão foi feita entre eles, e de mesmo modo com os outros lados.
Entretanto, apenas a condição de proporcionalidade dos lados não é suficiente para afirmarmos a semelhança entre os dois triângulos. Necessitamos que seus ângulos correspondentes sejam iguais.
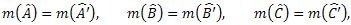
Sendo assim, indicaremos a semelhança destes triângulos desta forma:
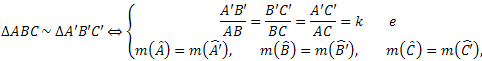
Se invertermos a afirmação feita acima, teremos um fato verdadeiro: as condições são satisfeitas somente quando os triângulos são semelhantes.
Vejamos um desenho para que possamos compreender melhor:

Antes, temos que determinar a correspondência dos vértices de cada triângulo, pois assim determinaremos a correspondência dos lados e dos ângulos entre estes dois triângulos.
Os vértices A, B, C correspondem, respectivamente, aos vértices A’, B’, C’. Sendo assim, montaremos as razões de proporcionalidade entre os lados correspondentes.
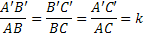
Uma das condições é que todos os lados correspondentes possuam uma proporcionalidade, que chamaremos neste caso de k. Ressaltando que essa razão foi construída pela divisão de cada lado correspondente: veja que o lado A’B’ do segundo triângulo corresponde ao lado AB do primeiro triângulo. Por este fato, a divisão foi feita entre eles, e de mesmo modo com os outros lados.
Entretanto, apenas a condição de proporcionalidade dos lados não é suficiente para afirmarmos a semelhança entre os dois triângulos. Necessitamos que seus ângulos correspondentes sejam iguais.
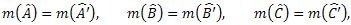
Sendo assim, indicaremos a semelhança destes triângulos desta forma:
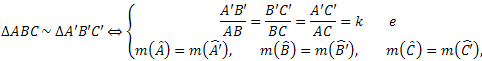
Exemplo:
Verifique se os triângulos a seguir são proporcionais.
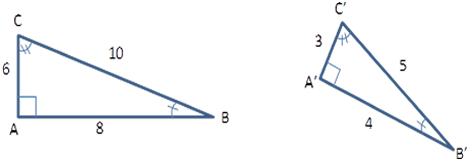
Ao verificarmos a congruência dos ângulos, teremos que:

Temos agora que verificar a proporcionalidade dos lados.
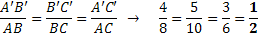
Note que todos os lados possuem a mesma razão de proporcionalidade (1/2).
Sendo assim, podemos afirmar que
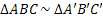
fonte:www.mundoeducacao.com
- Questão 36 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Seguem três afirmações sobre semelhança de polígonos: I. se os lados de dois triângulos são respectivamente paralelos dois a dois, então esses triângulos são semelhantes; II. todos os losangos que têm as medidas das duas diagonais iguais entre...
- Questão 80 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Observe as sentenças a seguir. I. Triângulos retângulos cujas hipotenusas medem a ? 2 unidades, sendo a um número real positivo, são semelhantes.II. Triângulos com todos os ângulos internos medindo 60º, são semelhantes.III. Triângulos com lados...
- Semelhança De Polígonos
Polígonos são regiões planas fechadas, constituídas de lados, vértices e ângulos. Dizemos que dois polígonos são semelhantes quando eles possuem o mesmo número de lados e se adéquam às seguintes condições: Ângulos iguais. Lados correspondentes...
- SemelhanÇa
Conceito: Duas figuras são semelhantes se tiverem a mesma forma (não importa o tamanho). EXEMPLOS Dizdemos que: -- Duas circunferências são sempre semelhantes.-- Dois quadrados são sempre semelhantes. TRIÂNGULO SEMELHANTES Observe...
- Semelhança
SEMELHANÇA Conceito: Duas figuras são semelhantes se tiverem a mesma forma (não importa o tamanho). EXEMPLOS Dizdemos que: -- Duas circunferências são sempre semelhantes.-- Dois quadrados são sempre semelhantes. TRIÂNGULO SEMELHANTES...
