Matemática

Sabemos que sistema linear é um conjunto de n equações lineares com n incógnitas relacionadas entre si. A solução de um sistema linear pode ser obtida de várias maneiras. Veremos uma das formas de resolução de um sistema utilizando a regra de Cramer.
Todo sistema linear pode ser associado a uma matriz envolvendo os coeficientes numéricos e a parte literal. Por exemplo, considere o seguinte sistema linear:
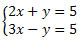
Sua representação matricial dos coeficientes das incógnitas é (matriz incompleta):
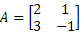
Já a representação matricial completa do sistema, levando em consideração somente os coeficientes numéricos, é:
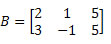
Todo o sistema pode ser representado matricialmente da seguinte forma:
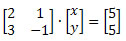
Diante da relação existente entre um sistema linear e uma matriz, Cramer desenvolveu um método de resolução de sistemas envolvendo as propriedades das matrizes e dos determinantes.
A regra de Cramer diz que: os valores das incógnitas de um sistema linear são dados por frações cujo denominador é o determinante da matriz dos coeficientes das incógnitas e o numerador é o determinante da matriz dos coeficientes das incógnitas após a substituição de cada coluna pela coluna que representa os termos independentes do sistema.
Vejamos um exemplo para melhor compreensão da regra de Cramer.
Exemplo: Encontre a solução do sistema abaixo utilizando a regra de Cramer.
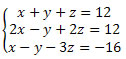
Solução: Primeiro, devemos escrever a matriz que representa os coeficientes das incógnitas e obter seu determinante.
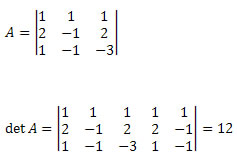
Em seguida, devemos excluir a primeira coluna da matriz dos coeficientes das incógnitas e substituí-la pelos termos independentes do sistema 12, 12 e – 16, e calcular o determinante.
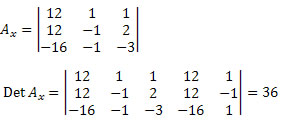
Agora, fazemos o mesmo com a segunda coluna da matriz dos coeficientes das incógnitas.
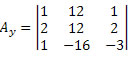
Calculando o determinante dessa matriz, obtemos:
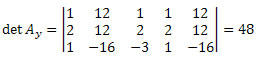
Repetindo o mesmo procedimento para a terceira coluna da matriz dos coeficientes das incógnitas, obtemos:
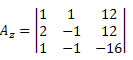
Fazendo o cálculo do determinante, teremos:

Segundo a regra de Cramer, temos que:
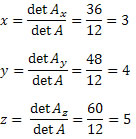
Assim, o conjunto solução do sistema é S = {(3, 4, 5)}.
- Regra De Cramer
A Regra de Cramer é um teorema em álgebra linear, que dá a solução de um sistema de equações lineares em termos de determinantes. Recebe este nome em homenagem a Gabriel Cramer (1704 - 1752). ...
- Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Escalonamento De Sistemas
Um sistema linear pode ser resolvido através do método da substituição ou cabelo método de Cramer, com o auxílio da régua de Sarrus. Uma nova forma de resolução será apresentada no intuito de ampliar as técnicas capaz de determinar os valores...
- Representação Matricial De Um Sistema
Um sistema de equações pode ser representado na forma de uma matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. O sistema terá a seguinte...
- Sistemas Pela Regra De Cramer
Um sistema de duas equações com duas incógnitas pode ser resolvido pelos seguintes métodos: adição e subtração. Os sistemas que apresentam três ou mais equações envolvendo três ou mais incógnitas também podem ser resolvidos pelos métodos...
Matemática
Sistema por Cramer

Resolvendo sistemas
Todo sistema linear pode ser associado a uma matriz envolvendo os coeficientes numéricos e a parte literal. Por exemplo, considere o seguinte sistema linear:
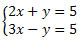
Sua representação matricial dos coeficientes das incógnitas é (matriz incompleta):
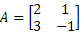
Já a representação matricial completa do sistema, levando em consideração somente os coeficientes numéricos, é:
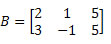
Todo o sistema pode ser representado matricialmente da seguinte forma:
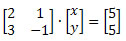
Diante da relação existente entre um sistema linear e uma matriz, Cramer desenvolveu um método de resolução de sistemas envolvendo as propriedades das matrizes e dos determinantes.
A regra de Cramer diz que: os valores das incógnitas de um sistema linear são dados por frações cujo denominador é o determinante da matriz dos coeficientes das incógnitas e o numerador é o determinante da matriz dos coeficientes das incógnitas após a substituição de cada coluna pela coluna que representa os termos independentes do sistema.
Vejamos um exemplo para melhor compreensão da regra de Cramer.
Exemplo: Encontre a solução do sistema abaixo utilizando a regra de Cramer.
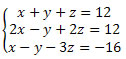
Solução: Primeiro, devemos escrever a matriz que representa os coeficientes das incógnitas e obter seu determinante.
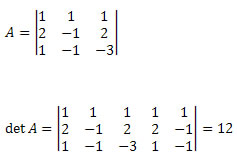
Em seguida, devemos excluir a primeira coluna da matriz dos coeficientes das incógnitas e substituí-la pelos termos independentes do sistema 12, 12 e – 16, e calcular o determinante.
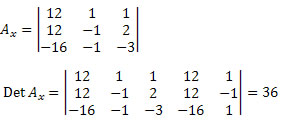
Agora, fazemos o mesmo com a segunda coluna da matriz dos coeficientes das incógnitas.
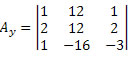
Calculando o determinante dessa matriz, obtemos:
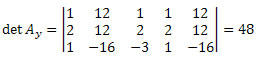
Repetindo o mesmo procedimento para a terceira coluna da matriz dos coeficientes das incógnitas, obtemos:
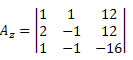
Fazendo o cálculo do determinante, teremos:

Segundo a regra de Cramer, temos que:
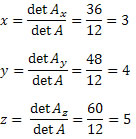
Assim, o conjunto solução do sistema é S = {(3, 4, 5)}.
- Regra De Cramer
A Regra de Cramer é um teorema em álgebra linear, que dá a solução de um sistema de equações lineares em termos de determinantes. Recebe este nome em homenagem a Gabriel Cramer (1704 - 1752). ...
- Regra De Cramer
Dado o sistema: 2x + 8y = 0 9x + 6y = 15 Notemos que a matriz incompleta desse sistema é: 2 8 9 6 Onde o determinante é dado por D = 2*6 – 8*9 →12 – 72 → – 60 Verificamos que o D ≠ 0, então o sistema é possível e determinado. A...
- Escalonamento De Sistemas
Um sistema linear pode ser resolvido através do método da substituição ou cabelo método de Cramer, com o auxílio da régua de Sarrus. Uma nova forma de resolução será apresentada no intuito de ampliar as técnicas capaz de determinar os valores...
- Representação Matricial De Um Sistema
Um sistema de equações pode ser representado na forma de uma matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. O sistema terá a seguinte...
- Sistemas Pela Regra De Cramer
Um sistema de duas equações com duas incógnitas pode ser resolvido pelos seguintes métodos: adição e subtração. Os sistemas que apresentam três ou mais equações envolvendo três ou mais incógnitas também podem ser resolvidos pelos métodos...
