Matemática
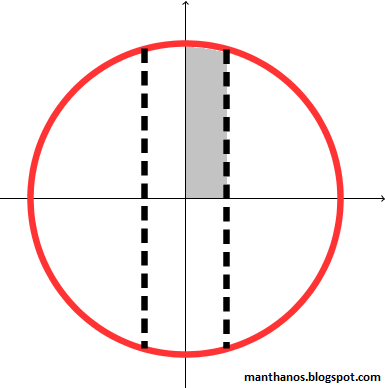
Conforme visto em postagem anterior, a área hachurada acima pode ser interpretada como uma integral definida. Mais precisamente, chamando de c a intercessão do semi-eixo positivo de x com a linha tracejada, o valor numérico da referida área é dado pela seguinte integral:

Assim, tudo o que os estudantes precisaram fazer foi encontrar c tal que:

+36\sin\left%20(2\arcsin\left%20(\frac{c}{12}%20\right%20)%20\right%20)=12\pi)

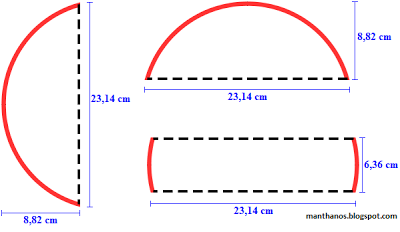
A pizza foi, portanto, fatiada de acordo com as seguintes medidas:
- Pizzas Na Reta Da Bailarina
Semana passada, em algumas das minhas escolas, decidi (com muito receio) começar a trabalhar a divisão com meus alunos de terceiro ano. Decidi usar uma ideia que eu mesma acho muito interessante: a ideia de que entre números há infinitos outros números....
- Integração Por Partes (exercício Resolvido)
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas). Revisarei os conteúdos e, se for necessário,...
- A área Do Círculo: Uma Demonstração
Esta postagem se dedica a demonstrar a conhecida fórmula que fornece a área de um círculo em função do seu raio. Para tanto vamos utilizar conceitos de trigonometria, geometria analítica e cálculo diferencial e integral - em especial a técnica...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\displaystyle \int \cos(ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \cos(ax)dx = \frac{\text{sen}(ax)}{a}+C \end{equation*} onde $a \in \mathbb{R}$ e $a\neq 0$. Seja a integral: \begin{equation*} I = \int \cos(ax)dx \end{equation*} Para o integrando $\cos(ax)$,...
Matemática
Solucionando o problema do corte da pizza
[veja o problema aqui]
Notemos, inicialmente, que por se tratarem de estudantes de matemática, eles deviam ter uma boa calculadora e, além disso, conhecimentos de cálculo integral.
O que os alunos fizeram, num primeiro momento, foi inserir um sistema de coordenadas cuja origem coincidiu com o centro da pizza:

Ao fazer isso eles subdividiram, evidentemente, a fatia central em 4 partes de mesma área. É óbvio que cada uma das 4 partes da fatia central equivale à 1/12 da área da pizza (pois a fatia toda equivale a 1/3 da pizza). Deste modo, uma vez que a área da pizza vale ?r², eles sabiam que área hachurada abaixo deveria valer exatamente ?r²/12:

Ao fazer isso eles subdividiram, evidentemente, a fatia central em 4 partes de mesma área. É óbvio que cada uma das 4 partes da fatia central equivale à 1/12 da área da pizza (pois a fatia toda equivale a 1/3 da pizza). Deste modo, uma vez que a área da pizza vale ?r², eles sabiam que área hachurada abaixo deveria valer exatamente ?r²/12:

Conforme visto em postagem anterior, a área hachurada acima pode ser interpretada como uma integral definida. Mais precisamente, chamando de c a intercessão do semi-eixo positivo de x com a linha tracejada, o valor numérico da referida área é dado pela seguinte integral:
Calculando a integral acima (e lembrando que neste caso r = 12) o problema se reduziu a encontrar c que satisfizesse a seguinte equação:
Usando um software (ou uma boa calculadora), eles encontraram que:

É bem provável que depois de tudo isso a fome tenha aumentado!!!
(para detalhes sobre como integrar a função acima veja esta postagem, na qual ela foi detalhadamente resolvida).
Observação: talvez o leitor se sinta frustrado com a solução apresentada devido ao fato dela fazer uso de um software (em vez de utilizar algum outro procedimento como, por exemplo, um método numérico). Entretanto, o nosso interesse repousou em obter uma equação que traduzisse as condições especificadas no enunciado. A despeito disso não ter ficado claro desde o princípio (o que deveria ter ocorrido!) a equação acima (cuja incógnita é c) cumpre o propósito agora (e tardiamente) mencionado.
Referências: livros de cálculo.
Erros podem ser relatados aqui.
- Pizzas Na Reta Da Bailarina
Semana passada, em algumas das minhas escolas, decidi (com muito receio) começar a trabalhar a divisão com meus alunos de terceiro ano. Decidi usar uma ideia que eu mesma acho muito interessante: a ideia de que entre números há infinitos outros números....
- Integração Por Partes (exercício Resolvido)
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas). Revisarei os conteúdos e, se for necessário,...
- A área Do Círculo: Uma Demonstração
Esta postagem se dedica a demonstrar a conhecida fórmula que fornece a área de um círculo em função do seu raio. Para tanto vamos utilizar conceitos de trigonometria, geometria analítica e cálculo diferencial e integral - em especial a técnica...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\displaystyle \int \cos(ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \cos(ax)dx = \frac{\text{sen}(ax)}{a}+C \end{equation*} onde $a \in \mathbb{R}$ e $a\neq 0$. Seja a integral: \begin{equation*} I = \int \cos(ax)dx \end{equation*} Para o integrando $\cos(ax)$,...
