Matemática
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas).
PERGUNTA
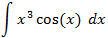
Neste caso você terá que aplicar integração por partes sucessivamente.
$$ \int x^3 \cos(x) \; dx$$
Comece escolhendo, apropriadamente, u e dv:
u = x³ dv = cos(x) dx
$$ \int u \cdot dv = u \cdot v - \int v \cdot du$$
$$ \int x^3 \cdot \cos(x) \; dx = x^3 \cdot \sin(x) - \int \sin(x) \cdot 3x^2 \; dx$$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3\int \sin(x) \cdot x^2 \; dx \; \; \; \;(1)$$
du = 2x dx v = ?cos(x)
Colocando na fórmula, você obtém:
$$ \int \sin(x) \cdot x^2 \; dx = x^2 \cdot (-\cos(x)) - \int -\cos(x) \cdot 2x \; dx$$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) - 2\int -\cos(x) \cdot x \; dx$$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2\int \cos(x) \cdot x \; dx \; \; \; \; (2)$$
Faça, mais uma vez, integração por partes para a integral que aparece no fim da expressão (2). Desta vez use a seguinte substituição:
u = x dv = cos(x) dx
du = dx v = sen(x)
Colocando na fórmula:
$$ \int \cos(x) \cdot x \; dx = x \cdot \sin(x) - \int \sin(x) \; dx $$
$$ \int \cos(x) \cdot x \; dx = x \sin(x) - (-\cos(x)) $$
$$ \int \cos(x) \cdot x \; dx = x \sin(x) + \cos(x) \; \; \; \; (3)$$
Agora, substitua (3) em (2):
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2\int \cos(x) \cdot x \; dx $$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2(x \sin(x) + \cos(x)) $$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2x \sin(x) + 2\cos(x) $$
Por fim, substitua este último resultado em (1):
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3\int \sin(x) \cdot x^2 \; dx $$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3(-x^2 \cos(x) + 2x \sin(x) + 2 \cos(x)) $$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) + 3x^2 \cos(x) - 6x \sin(x) - 6 \cos(x) $$
$$ \int x^3 \cos(x) \; dx = (x^3 - 6x) \sin(x) + (3x^2 - 6) \cos(x) $$
E não se esqueça de somar a constante de integração:
$$ \int x^3 \cos(x) \; dx = (x^3 - 6x) \sin(x) + (3x^2 - 6) \cos(x) + C$$
- Operações Com Notação Científica
Adição e Subtração Para somar ou subtrair dois números em notação científica, é necessário que os expoentes sejam o mesmo. Ou seja, um dos valores deve ser transformado para que seu expoente seja...
- Solucionando O Problema Do Gato E Rato (parte 3)
Na última postagem desta série paramos no ponto de resolver a seguinte equação diferencial:Resolvendo, obtemos o seguinte desenvolvimento:A partir daqui, temos dois casos a considerar: o caso em que c = 1 e o caso em que c ? 1. Observe que se c =...
- A Existência De "e"
Nesse post iremos tratar do famoso número de Euler , assim chamado em homenagem ao matemático suiço Leonard Euler, e o mesmo é a base dos logaritmos naturais. Iremos mostrar sua existência e que é limitado, . Definimos como sendo...
- A Função Erro E Outras Funções Relacionadas
Por:Kleber KilhianPaulo Sérgio Costa Lino A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:$$\int e^{-t^2}dt$$ Mais tarde, Kramp...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
Matemática
Integração por partes (exercício resolvido)
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas).
Revisarei os conteúdos e, se for necessário, farei adaptações e/ou acrescentarei mais informações e/ou corrigirei erros e/ou mudarei ligeiramente o modo de organizar as soluções (que aliás, foram julgadas "5 estrelas" pelos perguntantes).
O objetivo é apresentar um conteúdo possivelmente útil aos estudantes em uma notação mais adequada e que, portanto, proporciona uma leitura mais aprazível. Começarei com um exercício de Cálculo.
O objetivo é apresentar um conteúdo possivelmente útil aos estudantes em uma notação mais adequada e que, portanto, proporciona uma leitura mais aprazível. Começarei com um exercício de Cálculo.
PERGUNTA
Integração por partes?
Estou aprendendo integração por partes e gostaria, se possível, da resolução do seguinte exercício:
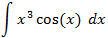
Outra coisa que eu não entendo é a diferença, no cálculo, de uma integral definida para indefinida por exemplo: Integral de cos(x) dx, se indefinida o resultado seria ?sen(x) + c, certo? No entanto, quando definida em um intervalo, por exemplo, entre 1 e 2, o resultado é outro. Grato pela ajuda :)
RESPOSTA
$$ \int x^3 \cos(x) \; dx$$
Comece escolhendo, apropriadamente, u e dv:
u = x³ dv = cos(x) dx
du = 3x² dx v = sen(x)
Substitua na fórmula da integração por partes:$$ \int u \cdot dv = u \cdot v - \int v \cdot du$$
$$ \int x^3 \cdot \cos(x) \; dx = x^3 \cdot \sin(x) - \int \sin(x) \cdot 3x^2 \; dx$$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3\int \sin(x) \cdot x^2 \; dx \; \; \; \;(1)$$
Agora você tem que calcular (novamente por partes) aquela integral que apareceu no fim da expressão (1). Para tanto, faça a seguinte escolha:
u = x² dv = sen(x) dxdu = 2x dx v = ?cos(x)
Colocando na fórmula, você obtém:
$$ \int \sin(x) \cdot x^2 \; dx = x^2 \cdot (-\cos(x)) - \int -\cos(x) \cdot 2x \; dx$$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) - 2\int -\cos(x) \cdot x \; dx$$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2\int \cos(x) \cdot x \; dx \; \; \; \; (2)$$
Faça, mais uma vez, integração por partes para a integral que aparece no fim da expressão (2). Desta vez use a seguinte substituição:
u = x dv = cos(x) dx
du = dx v = sen(x)
Colocando na fórmula:
$$ \int \cos(x) \cdot x \; dx = x \cdot \sin(x) - \int \sin(x) \; dx $$
$$ \int \cos(x) \cdot x \; dx = x \sin(x) - (-\cos(x)) $$
$$ \int \cos(x) \cdot x \; dx = x \sin(x) + \cos(x) \; \; \; \; (3)$$
Agora, substitua (3) em (2):
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2\int \cos(x) \cdot x \; dx $$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2(x \sin(x) + \cos(x)) $$
$$ \int \sin(x) \cdot x^2 \; dx = -x^2 \cos(x) + 2x \sin(x) + 2\cos(x) $$
Por fim, substitua este último resultado em (1):
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3\int \sin(x) \cdot x^2 \; dx $$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) - 3(-x^2 \cos(x) + 2x \sin(x) + 2 \cos(x)) $$
$$ \int x^3 \cos(x) \; dx = x^3 \sin(x) + 3x^2 \cos(x) - 6x \sin(x) - 6 \cos(x) $$
$$ \int x^3 \cos(x) \; dx = (x^3 - 6x) \sin(x) + (3x^2 - 6) \cos(x) $$
E não se esqueça de somar a constante de integração:
$$ \int x^3 \cos(x) \; dx = (x^3 - 6x) \sin(x) + (3x^2 - 6) \cos(x) + C$$
Integral de cos(x) dx, se indefinida o resultado seria ?sen(x) + c, certo?
Corretíssimo!!
Corretíssimo!!No entanto, quando definida em um intervalo, por exemplo, entre 1 e 2, o resultado é outro.
A diferença é que a integral indefinida é uma família de funções, um conjunto de funções. Já a integral definida é um número específico, que pode inclusive ser interpretado como uma área ou um volume, desde que "o gráfico esteja desenhado acima do eixo-x" (no caso da área) ou "acima do plano-xy" (no caso do volume).
Referências: a pergunta foi extraída de Y!R e a resposta é uma versão daquela que apresentei ao perguntante (que, inclusive, lhe atribuiu pontuação máxima).
Erros podem ser relatados aqui.
Referências: a pergunta foi extraída de Y!R e a resposta é uma versão daquela que apresentei ao perguntante (que, inclusive, lhe atribuiu pontuação máxima).
Erros podem ser relatados aqui.
- Operações Com Notação Científica
Adição e Subtração Para somar ou subtrair dois números em notação científica, é necessário que os expoentes sejam o mesmo. Ou seja, um dos valores deve ser transformado para que seu expoente seja...
- Solucionando O Problema Do Gato E Rato (parte 3)
Na última postagem desta série paramos no ponto de resolver a seguinte equação diferencial:Resolvendo, obtemos o seguinte desenvolvimento:A partir daqui, temos dois casos a considerar: o caso em que c = 1 e o caso em que c ? 1. Observe que se c =...
- A Existência De "e"
Nesse post iremos tratar do famoso número de Euler , assim chamado em homenagem ao matemático suiço Leonard Euler, e o mesmo é a base dos logaritmos naturais. Iremos mostrar sua existência e que é limitado, . Definimos como sendo...
- A Função Erro E Outras Funções Relacionadas
Por:Kleber KilhianPaulo Sérgio Costa Lino A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:$$\int e^{-t^2}dt$$ Mais tarde, Kramp...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
