Matemática
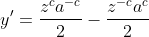

dz)
dz)
=\int\frac{z^ca^{-c}}{2}\;%20dz%20-\int%20\frac{z^{-c}a^c}{2}\;dz)
=\frac{a^{-c}}{2}\int%20z^c\;%20dz%20-\frac{a^c}{2}\int%20z^{-c}\;dz)
=\frac{a^{-c}}{2}\cdot%20\frac{z^{1+c}}{1+c}-\frac{a^c}{2}\cdot%20\frac{z^{1-c}}{1-c}+M)
=\frac{a^{-c}}{2}\cdot \frac{a^{1+c}}{1+c}-\frac{a^{c}}{2}\cdot\frac{a^{1-c}}{1-c}+M=\frac{1}{2}\left (\frac{a}{1+c}-\frac{a}{1-c} \right )+M)
=\frac{1}{2}\left (\frac{a(1-c)-a(1+c)}{(1+c)(1-c)} \right )+M=\frac{1}{2}\left (\frac{a-ac-a-ac)}{1-c^2} \right )+M)
=\frac{1}{2}\cdot\left (\frac{-2ac}{1-c^2} \right )+M=\frac{-ac}{1-c^2}+M=\frac{ac}{c^2-1}+M)

=\frac{a^{-c}}{2}\cdot%20\frac{z^{1+c}}{1+c}-\frac{a^c}{2}\cdot%20\frac{z^{1-c}}{1-c}-\frac{ac}{c^2-1})
=\frac{a^{-1}}{2}\int%20z%20\;%20dz-\frac{a^}{2}\int%20\frac{1}{z}%20\;%20dz)
=\frac{a^{-1}}{2}\cdot%20\frac{z^2}{2}-\frac{a}{2}\cdot%20\ln%20z%20+N)
Novamente, podemos obter o valor da constante de integração N calculando y(a):=\frac{a^{-1}}{2}\cdot%20\frac{a^2}{2}-\frac{a}{2}\cdot%20\ln%20a%20+N)
=\frac{a}{4}-\frac{a}{2}\cdot%20\ln%20a%20+N)

=\frac{a^{-1}}{2}\cdot%20\frac{z^2}{2}-\frac{a}{2}\cdot%20\ln%20z%20+\frac{a}{2}\cdot\ln%20a-\frac{a}{4})
- Exercício De Cálculo Resolvido Passo A Passo - Diferencial Total (dúvida Do Leitor)
Atendendo o pedido de um leitor, apresento nesta postagem solução para o seguinte Problema: utilize diferencial total para aproximar o valor deSolução: a expressão do diferencial total é dada porInspirados por (*), vamos considerar uma função...
- Integração Por Partes (exercício Resolvido)
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas). Revisarei os conteúdos e, se for necessário,...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Solucionando O Problema Do Gato E Rato (parte 2)
Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:Observemos, inicialmente, que o valor de f em a é 0, ou seja, f(a) = 0. Isto é fácil ver, basta olhar para a figura: Além...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
Matemática
Solucionando o Problema do Gato e Rato (parte 3)
Na última postagem desta série paramos no ponto de resolver a seguinte equação diferencial:
Resolvendo, obtemos o seguinte desenvolvimento:
A partir daqui, temos dois casos a considerar: o caso em que c = 1 e o caso em que c ? 1. Observe que se c = 1, então a função da segunda integral é 1/z e, portanto, a regra da potência não se aplica. Por outro lado, se c ? 1, então a regra da potência pode ser aplicada normalmente. Vamos considerar, inicialmente, o caso em que c ? 1 (aplicando a regra da potência):
Podemos obter o valor de M (constante de integração) calculando y(a):
Uma vez que y(a) = 0, obtemos:
E, portanto:
Vamos, agora, considerar o caso em que c = 1. Nesta situação, obtemos:
Novamente, podemos obter o valor da constante de integração N calculando y(a):
Uma vez que y(a) = 0, obtemos:
Portanto:
Agora, tudo o que nos resta é responder às questões propostas. Isto faremos na última postagem da série.
Referências: na última postagem da série.
Relate erros aqui.
- Exercício De Cálculo Resolvido Passo A Passo - Diferencial Total (dúvida Do Leitor)
Atendendo o pedido de um leitor, apresento nesta postagem solução para o seguinte Problema: utilize diferencial total para aproximar o valor deSolução: a expressão do diferencial total é dada porInspirados por (*), vamos considerar uma função...
- Integração Por Partes (exercício Resolvido)
Com esta postagem dou início a uma série na qual vou transcrever as soluções que outrora apresentei para questões feitas em um fórum de perguntas e respostas (a saber, no site Yahoo Respostas). Revisarei os conteúdos e, se for necessário,...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Solucionando O Problema Do Gato E Rato (parte 2)
Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:Observemos, inicialmente, que o valor de f em a é 0, ou seja, f(a) = 0. Isto é fácil ver, basta olhar para a figura: Além...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
