Matemática
Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:![zf''(z) =\frac{v}{u}\;\sqrt{1+[f'(z)]^2}](http://latex.codecogs.com/gif.latex?zf''(z)%20=\frac{v}{u}\;\sqrt{1+[f'(z)]^2}) Observemos, inicialmente, que o valor de f em a é 0, ou seja, f(a) = 0. Isto é fácil ver, basta olhar para a figura:
Observemos, inicialmente, que o valor de f em a é 0, ou seja, f(a) = 0. Isto é fácil ver, basta olhar para a figura:
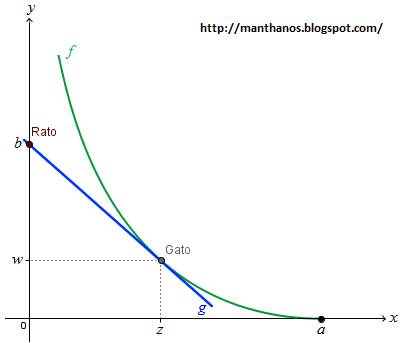 Além disso, quando o gato está em (a, 0) a direção de sua rota é vertical, ou seja, a inclinação da reta azul é zero. Isto significa que f '(a) = 0 (pois, conforme vimos em postagem anterior, a inclinação desta reta num dado ponto é, justamente, a tangente de f naquele ponto). Este fato também se percebe olhando para a figura:
Além disso, quando o gato está em (a, 0) a direção de sua rota é vertical, ou seja, a inclinação da reta azul é zero. Isto significa que f '(a) = 0 (pois, conforme vimos em postagem anterior, a inclinação desta reta num dado ponto é, justamente, a tangente de f naquele ponto). Este fato também se percebe olhando para a figura:
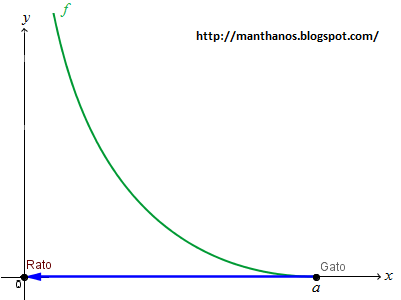 Antes de prosseguir façamos uma mudança na notação para simplificar a escrita. Vamos colocar f '(z) = y'(z) = y', f ''(z) = y''(z) = y'' e v/u = c, obtendo:
Antes de prosseguir façamos uma mudança na notação para simplificar a escrita. Vamos colocar f '(z) = y'(z) = y', f ''(z) = y''(z) = y'' e v/u = c, obtendo:
![zy''=c\sqrt{1+[y']^2}](http://latex.codecogs.com/gif.latex?zy''=c\sqrt{1+[y']^2}) Podemos reescrever a equação acima (que é de segunda ordem, pois o grau da derivada de mais alta ordem que nela aparece é 2) como uma equação de variáveis separáveis de primeira ordem. Para tanto, façamos a seguinte substituição:
Podemos reescrever a equação acima (que é de segunda ordem, pois o grau da derivada de mais alta ordem que nela aparece é 2) como uma equação de variáveis separáveis de primeira ordem. Para tanto, façamos a seguinte substituição: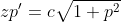



=c\ln%20z+K)
Pelas propriedades dos logaritmos:=\ln%20z^c+K)
}=e^{\ln%20z^c+K})

![y'(z)+\sqrt{1+[y'(z)]^2}=z^cK_2](http://latex.codecogs.com/gif.latex?y'(z)+\sqrt{1+[y'(z)]^2}=z^cK_2)
![y'(a)+\sqrt{1+[y'(a)]^2}=a^cK_2](http://latex.codecogs.com/gif.latex?y'(a)+\sqrt{1+[y'(a)]^2}=a^cK_2)
Agora usamos o fato de que y'(a) = 0:


![y'(z)+\sqrt{1+[y'(z)]^2}=z^ca^{-c}](http://latex.codecogs.com/gif.latex?y'(z)+\sqrt{1+[y'(z)]^2}=z^ca^{-c})
- Edo Linear De Primeira Ordem: Exercícios Resolvidos (passo A Passo) / Parte 2
Atendendo ao pedido de um leitor, apresentarei solução para o seguinte Problema: resolva a seguinte EDO linear: $$x^2\frac{dy}{dx}+2xy=e^x$$ Solução: Usarei a terminologia e a notação empregadas nesta postagem. Portanto, para melhor...
- Edo Linear De Primeira Ordem: Exercícios Resolvidos (passo A Passo) / Parte 1
Uma EDO linear de primeira ordem tem o seguinte formato: $$y'+P(x)y=Q(x)$$ Chamaremos a forma acima de "forma padrão" da equação (o $$Q(x)$$ é uma expressão na qual o símbolo $$y$$ não aparece). Quando vamos resolver uma EDO desta natureza,...
- Exercício De Cálculo Resolvido Passo A Passo - Diferencial Total (dúvida Do Leitor)
Atendendo o pedido de um leitor, apresento nesta postagem solução para o seguinte Problema: utilize diferencial total para aproximar o valor deSolução: a expressão do diferencial total é dada porInspirados por (*), vamos considerar uma função...
- Solucionando O Problema Do Gato E Rato (parte 3)
Na última postagem desta série paramos no ponto de resolver a seguinte equação diferencial:Resolvendo, obtemos o seguinte desenvolvimento:A partir daqui, temos dois casos a considerar: o caso em que c = 1 e o caso em que c ? 1. Observe que se c =...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
Matemática
Solucionando o Problema do Gato e Rato (parte 2)
Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:


y' = p
y'' = p'
y'' = p'
Substituindo obtemos:
Utilizando a, assim chamada, "notação de Leibniz" para a derivada:
Separando as variáveis:
Integrando ambos os lados:
Pelas regras de integração obtemos:
Pelas propriedades dos logaritmos:
Tomando a exponencial de ambos os lados:
Pelas propriedades básicas das funções exponencias e logarítmicas (e colocando eK = K2):
Desfazendo a última substituição (ou seja, colocando p = y' = y'(z)):
A fim de obter o valor de K1 colocamos z = a nesta última igualdade:
Agora usamos o fato de que y'(a) = 0:
Segue-se da expressão acima que:
Portanto:
Com um pouco de manipulação algébrica podemos escrever y' explicitamente:
![y'+\sqrt{1+[y']^2}=z^ca^{-c}](http://latex.codecogs.com/gif.latex?y'+\sqrt{1+[y']^2}=z^ca^{-c})
![\sqrt{1+[y']^2}=z^ca^{-c}-y'](http://latex.codecogs.com/gif.latex?\sqrt{1+[y']^2}=z^ca^{-c}-y')
![1+[y']^2=\left (z^ca^{-c}-y' \right )^2](http://latex.codecogs.com/gif.latex?1+[y']^2=\left%20(z^ca^{-c}-y'%20\right%20)^2)
![1+[y']^2=z^{2c}a^{-2c}-2z^{c}a^{-c}y'+[y']^2](http://latex.codecogs.com/gif.latex?1+[y']^2=z^{2c}a^{-2c}-2z^{c}a^{-c}y'+[y']^2)
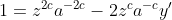
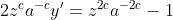
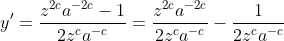
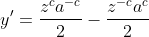
O próximo passo é resolver a equação diferencial acima. Isto faremos na próxima postagem da série.
Referências: na última postagem da série.
O próximo passo é resolver a equação diferencial acima. Isto faremos na próxima postagem da série.
Referências: na última postagem da série.
Relate erros aqui.
- Edo Linear De Primeira Ordem: Exercícios Resolvidos (passo A Passo) / Parte 2
Atendendo ao pedido de um leitor, apresentarei solução para o seguinte Problema: resolva a seguinte EDO linear: $$x^2\frac{dy}{dx}+2xy=e^x$$ Solução: Usarei a terminologia e a notação empregadas nesta postagem. Portanto, para melhor...
- Edo Linear De Primeira Ordem: Exercícios Resolvidos (passo A Passo) / Parte 1
Uma EDO linear de primeira ordem tem o seguinte formato: $$y'+P(x)y=Q(x)$$ Chamaremos a forma acima de "forma padrão" da equação (o $$Q(x)$$ é uma expressão na qual o símbolo $$y$$ não aparece). Quando vamos resolver uma EDO desta natureza,...
- Exercício De Cálculo Resolvido Passo A Passo - Diferencial Total (dúvida Do Leitor)
Atendendo o pedido de um leitor, apresento nesta postagem solução para o seguinte Problema: utilize diferencial total para aproximar o valor deSolução: a expressão do diferencial total é dada porInspirados por (*), vamos considerar uma função...
- Solucionando O Problema Do Gato E Rato (parte 3)
Na última postagem desta série paramos no ponto de resolver a seguinte equação diferencial:Resolvendo, obtemos o seguinte desenvolvimento:A partir daqui, temos dois casos a considerar: o caso em que c = 1 e o caso em que c ? 1. Observe que se c =...
- O Algoritmo Da Divisão Parte Ii
Nesta série de postagens estamos nos dedicando a demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
