Matemática
\;%20dx=F(b)-F(a) "\int_{a}^{b}f(x)\; dx=F(b)-F(a)")
=\sqrt{r^2-x^2} "f(x)=\sqrt{r^2-x^2}")
Para determinar a área de um circulo, podemos utilizar cálculo integral (calculando uma integral definida) e encontrar a área de uma das seguintes regiões:
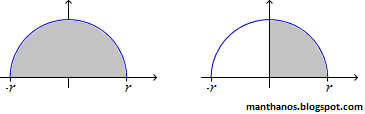Se escolhermos a primeira figura, deveremos calcular a seguinte integral definida (e obviamente multiplicar o resultado obtido por 2, visto a região hachurada equivale à metade da área do círculo):
\;dx "\int_{-r}^{r}f(x)\;dx")
Mas, por simplicidade, vamos escolher a segunda delas:
\;dx "\int_{0}^{r}f(x)\;dx")
Escolhemos esta integral devido ao fato de este zero como limite inferior nos facilitar a vida. É obvio que deveremos multiplicar o resultado final por 4 (pois a área hachurada equivale a um quarto da área total do círculo em questão).
Resumindo: se chamarmos de A a área de um cículo de raio r e centro na origem, teremos:
Mas, calculando esta integral definida, podemos mostrar que:
Portanto, segue-se que a área do círculo é dado por:
=\frac{x}{r} "\sin(\theta )=\frac{x}{r}")
 "x=r\sin(\theta )")
 "\frac{dx}{d\theta}=r\cos(\theta)")
A expressão acima pode ser arranjada da seguinte maneira (multiplicando ambos os lados por d?):
\; d\theta "dx=r\cos(\theta)\; d\theta")
)^2=r^2(\sin(\theta))^2=r^2\sin^2(\theta) "x^2=(r\sin(\theta))^2=r^2(\sin(\theta))^2=r^2\sin^2(\theta)")
Substituindo estes dois últimos resultados na integral, obtemos:
}\;r\cos(\theta)\;d\theta "\int \sqrt{r^2-x^2}\; dx=\int \sqrt{r^2-r^2\sin^2(\theta)}\;r\cos(\theta)\;d\theta")
Colocando r² em evidência (dentro do radical):
%20\right%20)}\;r\cos(\theta)\;d\theta "\int \sqrt{r^2\left (1-\sin^2(\theta) \right )}\;r\cos(\theta)\;d\theta")
"Tirando o r de dentro da raiz":
}\;r\cos(\theta)\;d\theta "\int r\sqrt{1-\sin^2(\theta)}\;r\cos(\theta)\;d\theta")
}\;r\cos(\theta)\;d\theta "\int r\sqrt{\cos^2(\theta)}\;r\cos(\theta)\;d\theta")
Extraindo a raiz quadrada do cosseno ao quadrado:
 \;r\cos(\theta)\;d\theta "\int r \cos(\theta) \;r\cos(\theta)\;d\theta")
Efetuando as multiplicações:
 \;d\theta "\int r^2 \cos^2(\theta) \;d\theta")
Tirando a constante r² para fora do sinal da integral (regra básica):
 \;d\theta "r^2\int \cos^2(\theta) \;d\theta")
Utilizando mais uma identidade trigonométrica (às vezes chamada "identidade de redução de potência"):
}{2} \;d\theta "r^2\int \frac{1 + \cos(2\theta)}{2} \;d\theta")
Por um procedimento que dispensa comentários:
}{2} \;d\theta "r^2\int \frac{1}{2}+ \frac{\cos(2\theta)}{2} \;d\theta")
Regra básica (a integral de uma soma é a soma das integrais):
}{2} \;d\theta \right ] "r^2\left [\int \frac{1}{2}\;d\theta+ \int \frac{\cos(2\theta)}{2} \;d\theta \right ]")
Novamente, tirando as constantes para fora das integrais:
\;d\theta \right ] "r^2\left [\frac{1}{2}\int d\theta+\frac{1}{2}\int \cos(2\theta)\;d\theta \right ]")
Aplicando a técnica da substituição na segunda integral, podemos fazer:
\;\frac{1}{2}\;dw \right ] "r^2\left [\frac{1}{2}\int d\theta+\frac{1}{2}\int \cos(w)\;\frac{1}{2}\;dw \right ]")
Novamente aplicando a regra da constante (na segunda integral):
\;dw \right ] "r^2\left [\frac{1}{2}\int d\theta+\frac{1}{4}\int \cos(w)\;dw \right ]")
Pelas regras básicas de integração:
\ \right ] "r^2\left [\frac{1}{2}\;\theta+\frac{1}{4}\;\sin(w)\ \right ]")
Aplicando a distributiva:
}{4} "\frac{r^2\theta}{2}+\frac{r^2 \sin(w)}{4}")
}{2}\;+\frac{r^2\sin(2\arcsin (\frac{x}{r}))}{4}\; "\frac{r^2\arcsin (\frac{x}{r})}{2}\;+\frac{r^2\sin(2\arcsin (\frac{x}{r}))}{4}\;")
}{2}\;+\frac{r^2\sin(2\arcsin(\frac{r}{r}))}{4}\; \right ]-\left [\frac{r^2\arcsin (\frac{0}{r})}{2}\;+\frac{r^2\sin(2\arcsin(\frac{0}{r}))}{4}\; \right ] "\small \dpi{100} \left [\frac{r^2\arcsin (\frac{r}{r})}{2}\;+\frac{r^2\sin(2\arcsin(\frac{r}{r}))}{4}\; \right ]-\left [\frac{r^2\arcsin (\frac{0}{r})}{2}\;+\frac{r^2\sin(2\arcsin(\frac{0}{r}))}{4}\; \right ]")
Simplificando as frações ("dentro dos arcsin"):
}{2}\;+\frac{r^2\sin(2\arcsin(1))}{4}\; \right ]-\left [\frac{r^2\arcsin (0)}{2}\;+\frac{r^2\sin(2\arcsin(0))}{4}\; \right ] "\small \dpi{100} \left [\frac{r^2\arcsin (1)}{2}\;+\frac{r^2\sin(2\arcsin(1))}{4}\; \right ]-\left [\frac{r^2\arcsin (0)}{2}\;+\frac{r^2\sin(2\arcsin(0))}{4}\; \right ]")
}{4}\; \right ]-\left [\frac{r^2\cdot0}{2}\;+\frac{r^2\sin(2\cdot0)}{4}\; \right ] "\left [\frac{r^2 \cdot\frac{\pi}{2}}{2}\;+\frac{r^2\sin(2\cdot\frac{\pi}{2})}{4}\; \right ]-\left [\frac{r^2\cdot0}{2}\;+\frac{r^2\sin(2\cdot0)}{4}\; \right ]")
Simplificando mais um pouco:
}{4}\; \right ]-\left [0+\frac{r^2\sin(0)}{4}\; \right ] "\left [\frac{\frac{\pi r^2}{2}}{2}\;+\frac{r^2\sin(\pi)}{4}\; \right ]-\left [0+\frac{r^2\sin(0)}{4}\; \right ]")
Simplificando a primeira fração, lembrando que sin ? = 0 e, como já dissemos, que sin 0 = 0, obtemos:
Assim, terminamos de mostrar que
E é precisamente isso o que queríamos fazer.
Referência: livros de cálculo.
Erros podem ser relatados aqui.
- Solucionando O Problema Do Corte Da Pizza
[veja o problema aqui] Notemos, inicialmente, que por se tratarem de estudantes de matemática, eles deviam ter uma boa calculadora e, além disso, conhecimentos de cálculo integral. O que os alunos fizeram, num primeiro momento, foi inserir um sistema...
- Integrais
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- A Integral Como Antiderivada
Na matemática aplicada ocorre frequentemente conhecermos a derivada de uma função e termos que encontrar a própria função. Por exemplo, podemos conhecer a velocidade $dx/dt$ de uma partícula e precisamos encontrar a equação do movimento $x=f(t)$,...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
Matemática
A área do círculo: uma demonstração
Esta postagem se dedica a demonstrar a conhecida fórmula que fornece a área de um círculo em função do seu raio. Para tanto vamos utilizar conceitos de trigonometria, geometria analítica e cálculo diferencial e integral - em especial a técnica de integração por substituição trigonométrica (desnecessário dizer que vamos lidar com funções de uma variável real). Vamos, então, ao que interessa:
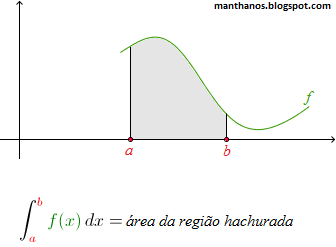
Grosso modo, o Teorema Fundamental do Cálculo (TFC) nos diz que se F é qualquer antiderivada (ou primitiva ou integral indefinida) de f, então:
É comum interpretarmos a integral acima (ou seja, a integral de f definida no intervalo [a, b]) como sendo numericamente igual a área de uma determinada região do plano, a saber, a área abaixo do gráfico de f, acima do eixo-x e limitada lateralmente pelas retas x = a e x = b:
(a interpretação acima vale, apenas, quando f(x) é positiva para todo x em [a, b])
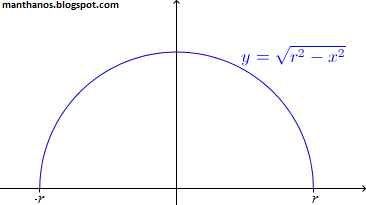
Da geometria analítica sabemos que uma circunferência de raio r e centro na origem (de um sistema de coordenadas cartesianas) pode ser dada pela equação x² + y² = r². Se convencionarmos, como de costume, que o símbolo ? denota apenas a raiz quadrada positiva de um valor, podemos dizer que uma semicircunferência (de centro na origem e raio r) pode ser dada pela seguinte equação:
Observe o gráfico da função y acima definida:
Tomemos, então a seguinte função:
Resumindo: se chamarmos de A a área de um cículo de raio r e centro na origem, teremos:
Então, para cumprirmos o nosso propósito basta mostrar que de fato aquela integral vale um quarto de ?r². E é isto o que vamos fazer agora (detalhadamente).
Com já vimos (na parte do TFC enunciada acima), para calcular uma integral definida precisamos de uma antiderivada de f. Isto significa que precisamos calcular a seguinte integral indefinida:
Com já vimos (na parte do TFC enunciada acima), para calcular uma integral definida precisamos de uma antiderivada de f. Isto significa que precisamos calcular a seguinte integral indefinida:
Aqui podemos utilizar a técnica da substituição, mais especificamente, a substituição trigonométrica. Para visualizarmos qual deve ser a substituição atente para o seguinte triângulo retângulo (onde colocamos a hipotenusa como sendo o raio do círculo e a variável x como sendo um dos catetos):
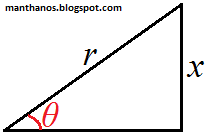Observe que a figura acima insere uma nova variável: o ângulo (que varia de acordo com a variação de x). Segue-se dela (da figura) que:
Na expressão acima, isolando o x obtemos:
Derivando a função acima (com relação à variável ?) o resultado será:
Olhe para a antepenúltima expressão. Observe que segue-se dela o seguinte resultado (quando elevamos ambos os lados à segunda potência):
Colocando r² em evidência (dentro do radical):
"Tirando o r de dentro da raiz":
Da trigonometria, conhecemos a "identidade pitagórica" sin²(?) + cos²(?) = 1 (que vale para um ângulo ? arbitrário). Pondo ? = ? e isolando o termo que contém o cosseno o resultado será cos²(?) = 1 - sin²(?) . Colocando isto na integral, obtemos:
Extraindo a raiz quadrada do cosseno ao quadrado:
Efetuando as multiplicações:
Tirando a constante r² para fora do sinal da integral (regra básica):
Utilizando mais uma identidade trigonométrica (às vezes chamada "identidade de redução de potência"):
Por um procedimento que dispensa comentários:
Regra básica (a integral de uma soma é a soma das integrais):
Novamente, tirando as constantes para fora das integrais:
Aplicando a técnica da substituição na segunda integral, podemos fazer:
Substituindo:
Novamente aplicando a regra da constante (na segunda integral):
Pelas regras básicas de integração:
Aplicando a distributiva:
Observe que temos um resultado em termos das variáveis ? e w. Mas nossa variável original é x, então precisamos voltar para elas antes de aplicar o TFC (pois os limites de integração 0 e r são dados em função de x. Poderíamos, alternativamente, reescrever os limites de integração em função das novas variáveis, mas preferimos a primeira opção). Lembrando, então, que w = 2? temos:
}{4} "\frac{r^2\theta}{2}+\frac{r^2\sin(2\theta)}{4}")
Lembrando agora que x = r sin(?) podemos isolar o sin(?), tomar o arcsin de ambos os lados e obter:
 "\theta=\arcsin\left (\frac{x}{r} \right )")
Lembrando agora que x = r sin(?) podemos isolar o sin(?), tomar o arcsin de ambos os lados e obter:
Fazendo esta substituição, obtemos, em fim, uma antiderivada de f:
É comum, após calcularmos uma integral indefinida, somarmos uma constante (por vezes chamada "constante de integração"). Contudo, neste caso não precisamos somar nada, pois para aplicar o TFC (que é nosso objetivo) precisamos de qualquer antiderivada de f, o que equivale a dizer que a constante de integração é totalmente arbitrária. Assim podemos, naturalmente, escolhê-la como sendo igual a zero.
Vamos então aplicar o TFC (enunciado logo no início desta postagem). Para isso, pegamos a expressão acima colocando r (limite superior) no lugar do x e dela subtraímos a mesma expressão, mas desta vez colocando o 0 (limite inferior) no lugar do x:
Vamos então aplicar o TFC (enunciado logo no início desta postagem). Para isso, pegamos a expressão acima colocando r (limite superior) no lugar do x e dela subtraímos a mesma expressão, mas desta vez colocando o 0 (limite inferior) no lugar do x:
Simplificando as frações ("dentro dos arcsin"):
Sabemos que sin ?/2 = 1, logo o arco cujo seno vale 1 é ?/2, ou seja, arcsin (1) = ?/2; também sabemos que sin 0 = 0, logo o arco cujo seno vale 0 é 0, ou seja, arcsin (0) = 0. Substituindo estes valores:
Simplificando mais um pouco:
Simplificando a primeira fração, lembrando que sin ? = 0 e, como já dissemos, que sin 0 = 0, obtemos:
Assim, terminamos de mostrar que
E é precisamente isso o que queríamos fazer.
Referência: livros de cálculo.
Erros podem ser relatados aqui.
- Solucionando O Problema Do Corte Da Pizza
[veja o problema aqui] Notemos, inicialmente, que por se tratarem de estudantes de matemática, eles deviam ter uma boa calculadora e, além disso, conhecimentos de cálculo integral. O que os alunos fizeram, num primeiro momento, foi inserir um sistema...
- Integrais
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- A Integral Como Antiderivada
Na matemática aplicada ocorre frequentemente conhecermos a derivada de uma função e termos que encontrar a própria função. Por exemplo, podemos conhecer a velocidade $dx/dt$ de uma partícula e precisamos encontrar a equação do movimento $x=f(t)$,...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...