Matemática
 [Figura 1]
[Figura 1]
Usamos a regra da derivada de um quociente, fazendo:
$$g'(x)=\frac{(x-1)-(x+1)}{(x-1)^2}=\frac{-2}{(x-1)^2}$$
Vejam que, se $g$ é uma antiderivada de $f$ sobre um conjunto $I$, então $g+C$ também o é, onde $C$ é uma constante qualquer. A razão é que se $D_xg(x)=f(x)$, então:
$$D_x[g(x)+C]=D_xg(x)+D_xC=f(x)+0=f(x)$$
Exemplo $2$: Sendo $\displaystyle g(x)=\frac{x}{1+x}$ uma antiderivada de $\displaystyle f(x)=\frac{1}{(1+x)^2}$, encontre um número infinito de antiderivadas de $f$.
Vamos definir $h=g+C$, onde $C$ é uma constante arbitrária. Assim:
$$h(x)=\frac{x}{1+x}+C=\frac{x+C+Cx}{1+x}$$
Teorema $1$: Antidiferenciação da função nula.
Seja $g$ uma função tal que $g'(x)=0$ vale para todos os valores de $x$ em algum intervalo aberto $I$. Então $g$ tem um valor constante em $I$.
Demonstração: Para esta demonstração, basta provar que o valor de $g$ em um número $a$ em $I$ é o mesmo valor de $g$ em qualquer outro ponto $b$ em $I$. Pelo Teorema do Valor Médio, existe um número $C$ entre $a$ e $b$ tal que:
$$g(b)-g(a)=g'(c)(b-a)=0(b-a)=0$$
Assim, $g(a)=g(b)$ finalizando nossa demonstração.
O teorema seguinte é uma consequência direta do Teorema $1$ e nos mostra como encontrar todas as antiderivadas de uma função em um intervalo aberto, desde que se conheça uma dessas derivadas.
Teorema $2$: Antidiferenciação em um intervalo aberto.
Notação para antiderivadas
Se $C$ é uma constante qualquer, então $g(x)+C$ também é uma antiderivada de $f$.
Definição $2$: Notação para integral de antiderivadas
Para verificar a afirmativa da forma: $\displaystyle \int f(x)dx=g(x)+C$ é necessário apenas verificar que $g'(x)=f(x)$ para todos os valores de $x$ no domínio de $f$.
Exemplo $4$: Verificar a equação dada: $\displaystyle \int x^2dx=\frac{1}{3}x^3+C$.
Solução: $\displaystyle D_x\left(\frac{1}{3}x^3 \right)=x^2$
Exemplo $5$: Verificar a equação: $\displaystyle \int dx=x+C$.
Solução: $\displaystyle \int dx= \int 1dx=x+C$, portanto, $D_x(x)=1$.
Métodos para integração:
Integração por Partes
Integração por Substituição
Integração por Substituição Trigonométrica
Integração por Frações Parciais - Fatores Lineares
Integração por Frações Parciais - Fatores Quadráticos Irredutíveis
Referências:
[1] Cálculo V1 - Munem - Foulis
[2] Notas de aula
Veja mais:
Leibniz e as Diferenciais
Os Mitos Leibzinianos a Respeito das Curvas Diferenciais
O Cálculo Integral: O Cálculo das Áreas

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Demonstração Dos Pontos De Máximo E Mínimo De Uma Função Quadrática
Veremos nesta postagem como determinar os pontos de máximo e mínimo de uma função de segundo grau. Definição $1$: Valor de máximoDizemos que o número $Y_M \in Im(f)$ é o valor de máximo da função $y=f(x)$ se, e somente se, $Y_M \geq y$, $\forall\...
Matemática
A Integral Como Antiderivada
Na matemática aplicada ocorre frequentemente conhecermos a derivada de uma função e termos que encontrar a própria função. Por exemplo, podemos conhecer a velocidade $dx/dt$ de uma partícula e precisamos encontrar a equação do movimento $x=f(t)$, ou podemos querer achar a função lucro de um certo produto quando conhecemos a margem de lucro. As soluções desses problemas necessitam que se desfaça a operação de diferenciação, isto é, temos que antidiferenciar.
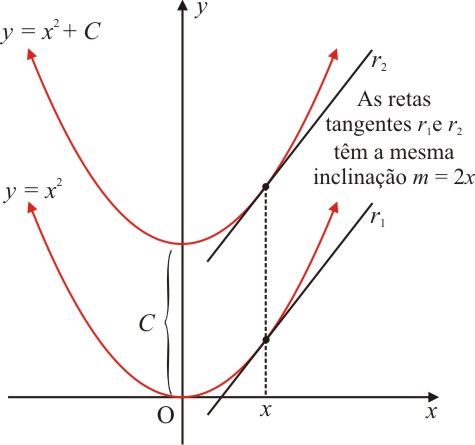
Se $f$ e $g$ são duas funções tais que $g'=f$, podemos dizer que $g$ é uma antiderivada de $f$. Assim $g(x)=x^2$ é uma antiderivada de $f(x)$, desde que $D_x(x^2)=2x$. Se $C$ é uma constante, então a função definida por $y=x^2+C$ também é uma antiderivada de $f$, desde que $D_x(x^2+C)=2x$. Geometricamente, se o gráfico de $y=x^2+C$ é obtido pela translação do gráfico de $y=x^2$ verticalmente de $C$ unidades, isso não muda a inclinação da reta tangente para um dado valor de $x$.

Definição $1$: Uma função $g$ é dita antiderivada (ou primitiva) de uma função $f$ sobre um conjunto de números $I$ se $g'(x)=f(x)$ para todos os valores de $x$ em $I$. O procedimento para achar antiderivadas é chamado antidiferenciação.
Se afirmarmos que $g$ é uma antiderivada de $f$ sem mencionar explicitamente o conjunto $I$, da definição $1$, fica subtendido que $I$ é todo o domínio de $f$, tal que $g'(x)=f(x)$ vale para todos os valores de $x$ no domínio de $f$.
Exemplo $1$: Vamos provar que $\displaystyle g(x)=\frac{x+1}{x-1}$ é uma antiderivada de $\displaystyle f(x)=\frac{-2}{(x-1)^2}$.
Usamos a regra da derivada de um quociente, fazendo:
$$g'(x)=\frac{(x-1)-(x+1)}{(x-1)^2}=\frac{-2}{(x-1)^2}$$
Vejam que, se $g$ é uma antiderivada de $f$ sobre um conjunto $I$, então $g+C$ também o é, onde $C$ é uma constante qualquer. A razão é que se $D_xg(x)=f(x)$, então:
$$D_x[g(x)+C]=D_xg(x)+D_xC=f(x)+0=f(x)$$
Portanto, após acharmos uma antiderivada $g$ de uma função $f$, temos automaticamente um infinito de antiderivadas de $f$ da forma $g+C$, onde $C$ é uma constante arbitrária.
Exemplo $2$: Sendo $\displaystyle g(x)=\frac{x}{1+x}$ uma antiderivada de $\displaystyle f(x)=\frac{1}{(1+x)^2}$, encontre um número infinito de antiderivadas de $f$.
Vamos definir $h=g+C$, onde $C$ é uma constante arbitrária. Assim:
$$h(x)=\frac{x}{1+x}+C=\frac{x+C+Cx}{1+x}$$
Quaisquer dessas funções $h$ é uma antiderivada de $f$. Desde que a derivada de uma função constante seja a função nula, segue que qualquer função constante é uma antiderivada da função nula.
Teorema $1$: Antidiferenciação da função nula.
Seja $g$ uma função tal que $g'(x)=0$ vale para todos os valores de $x$ em algum intervalo aberto $I$. Então $g$ tem um valor constante em $I$.
Demonstração: Para esta demonstração, basta provar que o valor de $g$ em um número $a$ em $I$ é o mesmo valor de $g$ em qualquer outro ponto $b$ em $I$. Pelo Teorema do Valor Médio, existe um número $C$ entre $a$ e $b$ tal que:
$$g(b)-g(a)=g'(c)(b-a)=0(b-a)=0$$
Assim, $g(a)=g(b)$ finalizando nossa demonstração.
O teorema seguinte é uma consequência direta do Teorema $1$ e nos mostra como encontrar todas as antiderivadas de uma função em um intervalo aberto, desde que se conheça uma dessas derivadas.
Teorema $2$: Antidiferenciação em um intervalo aberto.
Seja $g$ uma antiderivada da função $f$ no intervalo aberto $I$. Então uma função $h$ com domínio $I$ é uma antiderivada de $f$ em $I$ se e somente se $h=g+C$ para qualquer constante $C$.
Demonstração: Se $h=g+C$, então $h'=g'=f$, logo, $h$ é uma antiderivada de $f$ em $I$. Agora, vamos super que $h$ é uma antiderivada de $f$ em $I$, então a função $h-g$ satisfaz $(h-g)'=h'-g'=f-f=0$ no intervalo aberto $I$. Segue do Teorema $1$ que existe uma constante $C$ tal que $h-g=C$, isto é, $h=g+C$.
Exemplo $3$: Se a função $\displaystyle g(x)=\frac{1}{2}x^2$ é uma antiderivada da função $f(x)=x$, ache todas as antiderivadas de $f$.
Neste caso, o intervalo $I$ é $\mathbb{R}$. Pelo Teorema $2$, as antiderivadas de $f$ são todas as funções $h$ da forma $\displaystyle h(x)=\frac{1}{2}x^2+C$, onde $C$ é uma constante.
Notação para antiderivadas
As antiderivadas são tradicionalmente escritas usando-se um simbolismo especial que tem algumas vantagens da notação de Leibniz para derivadas e que foi usado pelo próprio Leibniz. O simbolismo pode ser compreendido pensando-se na diferencial $dy$ como uma porção infinitesimal de $y$ e imaginando que $y$ é a soma de todos esses infinitos. Leibniz usou uma letra $S$ estilizada: $\displaystyle \int$ para tais somatórios, tal que $\displaystyle y=\int dy$ deva simbolizar a ideia de que $y$ é a soma de todas sua diferenciais individuais.
Johann Bernoulli, um contemporâneo de Leibniz, sugeriu que o processo de reunir infinitésimos de forma a se ter uma quantidade inteira ou completa, como expresso por $\displaystyle y=\int dy$ deva ser convenientemente chamado de integração ao invés de somatório. A sugestão de Bernoulli foi aceita e hoje usamos o símbolo $\displaystyle \int$ como sinal de integração.
Vamos supor que $g$ é a antiderivada de $f$, tal que $g'=f$. Se tomarmos $y=g(x)$, então $dy=g'(x)dx=f(x)dx$, tal que:
$$y=\int dy=\int f(x)dx\text{ ; isto é, }g(x)=\int f(x)dx$$Se $C$ é uma constante qualquer, então $g(x)+C$ também é uma antiderivada de $f$.
Definição $2$: Notação para integral de antiderivadas
A notação $\displaystyle \int f(x)dx=g(x)+C$, onde $C$ é uma constante arbitrária, significa que a função $g$ é uma antiderivada da função $f$, tal que $g'(x)=f(x)$ vale para todos os valores de $x$ no domínio de $f$.
Se $I$ é um conjunto de números, a afirmativa de que $\displaystyle \int f(x)dx=g(x)+C$ e, $I$ (ou para $x$ em $I$), significa que $g$ é uma antiderivada de $f$ em $I$. Na definição $2$ a constante $C$ é chamada de constante de integração, o símbolo $\displaystyle \int$ é chamado de sinal da integral e a função $f$, ou a expressão $f(x)$ é chamada integrando da expressão $\displaystyle \int f(x)dx$. Também dizemos que $f(x)$ está sob o sinal da integral.
O processo para calcular $\displaystyle \int f(x)dx$, isto é, achar $g(x)+C$, é chamado de integração indefinida. Neste caso, indefinida é usado porque a constante $C$ pode assumir qualquer valor e portanto não é decididamente determinada pela função $f$. Por causa da natureza arbitrária da função $C$, a integral indefinida $\displaystyle \int f(x)dx$ não representa uma quantidade particular ou função. Portanto, devemos tomar certo cuidado ao manipular esta expressão.
Para verificar a afirmativa da forma: $\displaystyle \int f(x)dx=g(x)+C$ é necessário apenas verificar que $g'(x)=f(x)$ para todos os valores de $x$ no domínio de $f$.
Exemplo $4$: Verificar a equação dada: $\displaystyle \int x^2dx=\frac{1}{3}x^3+C$.
Solução: $\displaystyle D_x\left(\frac{1}{3}x^3 \right)=x^2$
Exemplo $5$: Verificar a equação: $\displaystyle \int dx=x+C$.
Solução: $\displaystyle \int dx= \int 1dx=x+C$, portanto, $D_x(x)=1$.
Métodos para integração:
Integração por Partes
Integração por Substituição
Integração por Substituição Trigonométrica
Integração por Frações Parciais - Fatores Lineares
Integração por Frações Parciais - Fatores Quadráticos Irredutíveis
Referências:
[1] Cálculo V1 - Munem - Foulis
[2] Notas de aula
Veja mais:
Leibniz e as Diferenciais
Os Mitos Leibzinianos a Respeito das Curvas Diferenciais
O Cálculo Integral: O Cálculo das Áreas

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral Indefinida Do Produto De Senos De Monômios De Coeficientes Angulares Diferentes
Neste artigo, veremos como encontrar uma fórmula para calcular a integral do produto de dois senos, cujos argumentos são monômios. Vamos demonstrar que: \begin{equation*} \int \text{sen}(ax) \cdot \text{sen}(bx)\ dx=\frac{\text{sen} [(a-b) x]}{2 (a-b)}...
- Demonstração Dos Pontos De Máximo E Mínimo De Uma Função Quadrática
Veremos nesta postagem como determinar os pontos de máximo e mínimo de uma função de segundo grau. Definição $1$: Valor de máximoDizemos que o número $Y_M \in Im(f)$ é o valor de máximo da função $y=f(x)$ se, e somente se, $Y_M \geq y$, $\forall\...
