Matemática
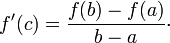
Referências
http://pt.wikipedia.org - Teorema do Valor Médio
- Equações Funcionais - Equação De Cauchy
Hoje vamos falar de um dos conceitos primordiais da teoria de Equações Funcionais, que é a equação de Cauchy. De fato, a Equação de Cauchy generaliza o conceito de operador linear: Se T for um operador linear definido na reta...
- Prova Geométrica Do Tfc
O leitor que já estudou Cálculo Diferencial e Integral provavelmente concorda que, no estudo desta disciplina, as interpretações geométricas de vários conceitos desempenham um papel bastante significativo. É de se notar, entretanto, que na hora...
- Questão: Aplicação Do Valor Intermediário
A questão que será apresentada aqui aborda mais uma das aplicações do Teorema do Valor Intermediário (para saber mais clique nessa postagem:As Consequências do Teorema do Valor Intermediário ), a questão foi enviada pelo leitor Arlyson A. Nascimento,...
- As Consequências Do Teorema Do Valor Intermediário
Olá, hoje iremos tratar de um resultado bastante simples (essa é minha opinião) em análise real, mas que possui bastantes aplicações, tanto em resolução de problemas de matemática quanto na prática. Esse resultado é o Teorema do Valor Intermediário,...
- As Equações De Cauchy-riemann
Seja f = u + iv uma função derivável num ponto z = x + iy. Então o quociente: Tem limite f ‘(z) com Δz –> à 0. Podemos fazer Δz tender a zero por valores reais Δz = k e, separadamente, por valores imaginários Δz = it. Obtemos,...
Matemática
Teorema do Valor Médio

Em matemática, o teorema do valor médio (também conhecido como Teorema de Lagrange) afirma que dada uma função contínua f definida num intervalo fechado [a,b] e diferenciável em (a,b), existe algum ponto c em (a,b) tal que :
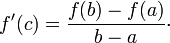
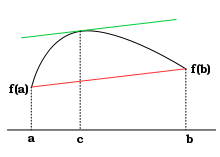
Geometricamente, isto significa que a tangente ao gráfico de f no ponto de abcissa c é paralela à secante que passa pelos pontos de abcissas a e b.
O teorema do valor médio também tem uma interpretação em termos físicos: se um objeto está em movimento e se a sua velocidade média é v, então, durante esse percurso (intervalo [a,b]), há um instante (ponto c) em que a velocidade instantânea também é v.
Demonstração
SejaFunções com Valores Vetoriais
Se f for uma função contínua de [a,b] em Rn que seja derivável em (a,b), então já não é verdade que existe necessariamente algum c ? (a,b) tal que
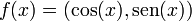 .
.
Generalização: Teorema de Cauchy

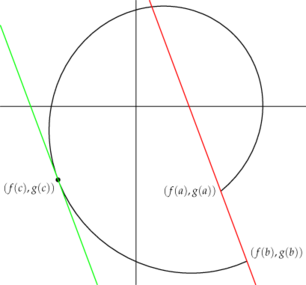
Um resultado mais geral é o Teorema de Cauchy, que afirma que se f e g são funções contínuas de [a,b] em R que são deriváveis em (a,b), então existe algum c ? (a,b) tal que
Referências
http://pt.wikipedia.org - Teorema do Valor Médio
- Equações Funcionais - Equação De Cauchy
Hoje vamos falar de um dos conceitos primordiais da teoria de Equações Funcionais, que é a equação de Cauchy. De fato, a Equação de Cauchy generaliza o conceito de operador linear: Se T for um operador linear definido na reta...
- Prova Geométrica Do Tfc
O leitor que já estudou Cálculo Diferencial e Integral provavelmente concorda que, no estudo desta disciplina, as interpretações geométricas de vários conceitos desempenham um papel bastante significativo. É de se notar, entretanto, que na hora...
- Questão: Aplicação Do Valor Intermediário
A questão que será apresentada aqui aborda mais uma das aplicações do Teorema do Valor Intermediário (para saber mais clique nessa postagem:As Consequências do Teorema do Valor Intermediário ), a questão foi enviada pelo leitor Arlyson A. Nascimento,...
- As Consequências Do Teorema Do Valor Intermediário
Olá, hoje iremos tratar de um resultado bastante simples (essa é minha opinião) em análise real, mas que possui bastantes aplicações, tanto em resolução de problemas de matemática quanto na prática. Esse resultado é o Teorema do Valor Intermediário,...
- As Equações De Cauchy-riemann
Seja f = u + iv uma função derivável num ponto z = x + iy. Então o quociente: Tem limite f ‘(z) com Δz –> à 0. Podemos fazer Δz tender a zero por valores reais Δz = k e, separadamente, por valores imaginários Δz = it. Obtemos,...

![\begin{array}{rccc}g\colon&[a,b]&\longrightarrow&\mathbb{R}\\&x&\mapsto&f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a).\end{array}](matematica/matematica-5631d1fd0922b.png)
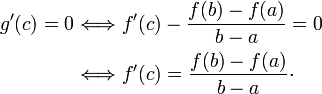
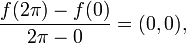
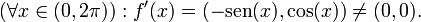
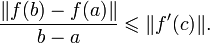
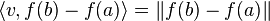
![\begin{array}{rccc}g\colon&[a,b]&\longrightarrow&\mathbb{R}\\&x&\mapsto&\langle v,f(x)-f(a)\rangle.\end{array}](matematica/matematica-5631d1ff48e1a.png)
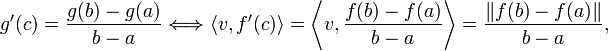
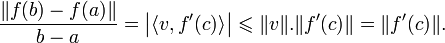
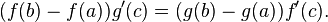
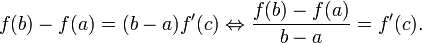
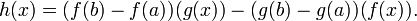
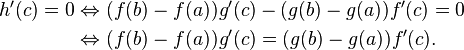
![\begin{array}{ccc}[a,b]&\longrightarrow&\mathbb{R}^2\\x&\mapsto&\bigl(f(x),g(x)\bigr),\end{array}](matematica/matematica-5631d2021bf68.png)