Matemática
De modo a contornar este problema, foram criados métodos iterativos de aproximações de raízes de funções com qualquer precisão pré-fixada.
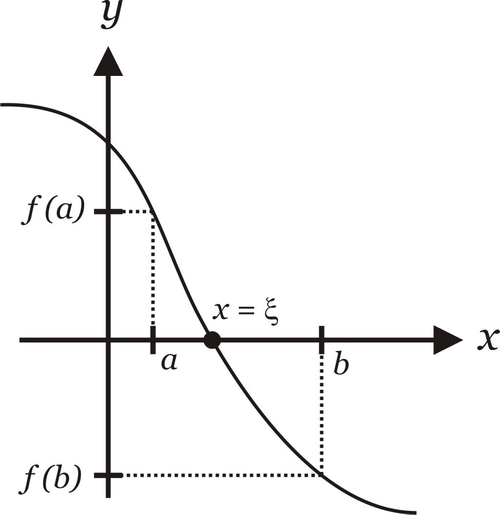
Inicialmente, temos que encontrar um intervalo $I=[a,b]$ cuja raiz está contida. Para tal, devemos fazer uma análise teórica da função. Podemos utilizar o seguinte teorema:
Dada a função $f(x)=x \log (x) - 1$, podemos construir uma tabela com vários valores para $x$ e analisar as mudanças de sinal de $f(x)$, encontrando um intervalo $I=[a,b]$:
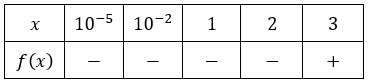 Vemos que o intervalo que contém pelo menos uma raiz é $I=[2,3]$.
Vemos que o intervalo que contém pelo menos uma raiz é $I=[2,3]$.
Podemos obter, a partir de uma função $f(x)$, uma função equivalente $g(x)=h(x)$, onde, ao analisarmos graficamente as duas funções, localizamos o ponto de intersecção entre as duas curvas e, assim, o intervalo $I$ que contém a raiz, sem precisar calcular $f(x)$.
\begin{equation*}
g(x) = 4 \cos (x) \quad \text{e} \quad h(x) = e^{2x}
\end{equation*}
Graficamente temos:
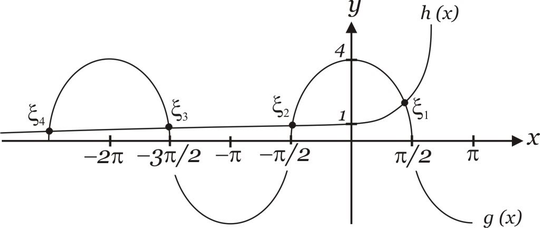 Notamos que as raízes:
Notamos que as raízes:
$\xi _1$ está no intervalo $I_1=[0, \pi]$;
$\xi_2$ está no intervalo $I_2=[-\pi, 0]$, para $k=1$;
$\xi_3$ está no intervalo $I_3=[-2\pi, -pi]$, para $k=2$;
$\xi_4$ está no intervalo $I_4=[-3\pi, -2\pi]$, para $k=2$.
Logo, as raízes são: $[0, \pi] \cup [-(k+1)\pi, 0 -k\pi], k \in \mathbb{Z}^+$.
\begin{equation*}
g(x)=x^3 \quad \text{e} \quad h(x)=9x-3
\end{equation*}
Graficamente temos:
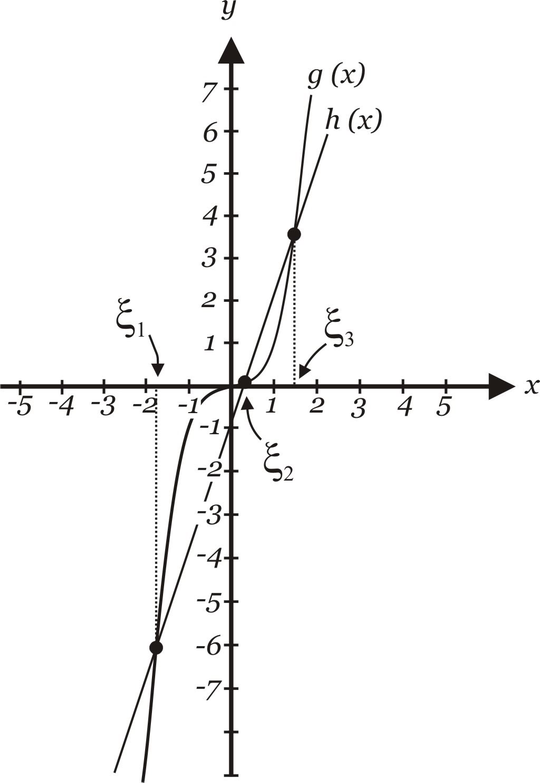
Notamos que as raízes:
$\xi_1$ está no intervalo $I_1=[-2,-1]$;
$\xi_2$ está no intervalo $I_2=[0,1]$;
$\xi_3$ está no intervalo $I_3=[1,2]$.
Vejam que desta forma encontramos os intervalos onde contém pelo menos uma raiz.
Existem métodos para aproximar raízes reais de funções reais, tais como o Método da Bissecção, Método da Posição Falsa, Método do Ponto Fixo; Método da Secante e Método de Newton-Raphson. Vamos estudar a seguir o Método de Newton-Raphson.
\begin{equation*}
f(x)=f(\overline{x})=f^\prime (\overline{x})(x-\overline{x})+f^{\prime \prime}(\xi (x))\cdot \frac{(x-\overline{x})^2}{2}
\end{equation*}
Se $x=p$:
\begin{equation*}
f(p)=f(\overline{x})=f^\prime (\overline{x})(p-\overline{x})+f^{\prime \prime}(\xi (p))\cdot \frac{(p-\overline{x})^2}{2}
\end{equation*}
Como $|p-\overline{x}| < \varepsilon$, e $\varepsilon$ é suficientemente pequeno, seu quadrado será ainda menor e tenderá a zero. Logo:
\begin{equation*}
f(p)=f(\overline{x}) + f^\prime(\overline{x})(p-\overline{x})\\
0=f(\overline{x})+ f^\prime(\overline{x})(p-\overline{x})
\end{equation*}
Que é a equação da reta tangente a $f(x)$ no ponto $\overline{x}$.
Isolando $p$:
\begin{equation*}
p=\overline{x} - \frac{f(\overline{x})}{f^\prime (\overline{x})}
\end{equation*}
Que nos leva ao algoritmo de Newton:
\begin{equation*}
x_{k+1}=x_k - \frac{f(x_k)}{f^\prime(x_k)}
\end{equation*}
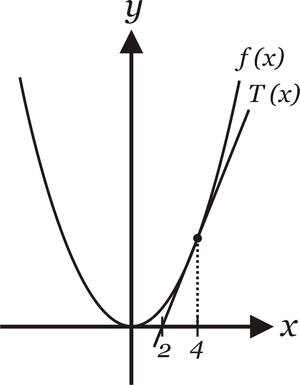
Observação: Seja a função $f(x)=x^2$, sua derivada será $f^\prime(x)=2x$. Qual é a equação da reta tangente no ponto igual a $4$?
\begin{equation*}
T(x)=f(\overline{x}) + f^\prime (\overline{x})(x-\overline{x})\\
T(x) = f(4) + f^\prime (4)(x-4)\\
T(x) = 16 + 8(x-4)
\end{equation*}
onde $T(x)$ é a tangente no ponto.
Graficamente temos:
Vejam que a cada iteração a raiz se aproxima mais da raiz real $\xi$.
\begin{equation*}
f(x)=x^2-6\
x^2-6=0\\
x^2=6\\
x=\sqrt{6}
\end{equation*}
Então, se $f(x)=x^2-6$ sua derivada será $f^\prime(x)=2x$.
Como a raiz quadrada de $6$ está localizada entre $2$ e $3$, podemos adotar um valor inical entre este intervalo ou em sua proximidade. Vamos adotar $1$ como valor inicial.
\begin{equation*}
x_{k+1} = x_k - \frac{f(x_k)}{f^\prime(x_k)}
\end{equation*}
Para $k_0 = 1$, temos:
\begin{equation*}
x_1 = x_0 - \frac{f(x_0)}{f^\prime(x_0)} = 1 - \frac{f(1)}{f^\prime (1)} = 1-\frac{5}{2} = 3,5
\end{equation*}
Para $k_1=3,5$, temos:
\begin{equation*}
x_2 = x_1 - \frac{f(x_1)}{f^\prime(x_1)} = 3,5 - \frac{f(3,5)}{f^\prime (3,5)} = 3,5 - \frac{6,25}{7} = 2,60714
\end{equation*}
Para $k_2=2,60714$, temos:
\begin{equation*}
x_3=x_2 - \frac{f(x_2)}{f^\prime(x_2)} = 2,60714 - \frac{f(2,60714)}{f^\prime (2,60714)} = 2,60714 - \frac{0,797178}{5,21418} = 2,45425638
\end{equation*}
Para $k_3 = 2,45425638$, temos:
\begin{equation*}
x_4 = x_3 - \frac{f(x_3)}{f^\prime(x_3)} = 2,45425638 - \frac{f(2,45425638)}{f^\prime (2,45425638)} = 2,45425638 - \frac{0,023374378}{4,90851276} = 2,449494413
\end{equation*}
Tomamos então $x_4$ como raiz aproximada de $f(x)$. E se fizermos a raiz quadrada de $6$ pela calculadora, notaremos que a raiz aproximada está correta até a quarta casa decimal.
Isso é fácil de verificar: sabemos que a derivada de uma função num ponto $x$ é a reta tangente À função neste ponto. Se o ponto $x$ é o ponto de mínimo, por exemplo, de uma função quadrática, a reta tangente $T(x)$ neste ponto será paralela ao eixo dos $x$.
Se analisarmos o algoritmo de Newton, veremos que o quociente entre a função e sua derivada será uma indeterminação, tendendo ao infinito.
\begin{equation*}
x_{k+1} = x_k - \frac{f(x_k)}{f^\prime (x_k)}
\end{equation*}
Para isso, devemos impor uma precisão inicial $\varepsilon$ para a raiz aproximada da função, tal que, se $f(x_k) < \varepsilon$, então para com as iterações e tome $\overline{x}$ como raiz aproximada de $f(x)$.
Seja $f(x)=0$ e sejam $f(x)$, $f^\prime (x)$ e $f^{\prime \prime}(x)$ contínuas num intervalo $I$ contendo a raiz $x=\xi$ de $f(x)=0$ e $f(\xi) \neq 0$.
$a)$ $x_0$: Aproximação inicial;
$b)$ $\varepsilon _1$ e $\varepsilon _2$ precisões.
Fim
Senão:
$k=1$
Fim
Senão:
Volte à etapa $4$
O método ideal para aproximação de raízes é aquele que a convergência é assegurada, e rápida, e que haja um número mínimo de iterações. Dentre os métodos, o Método de Newton é o mais indicado sempre que for fácil verificar as condições de convergência de $f(x)$ e que o cálculo de sua derivada não seja muito elaborado.
Para encontrarmos a raiz quadrada de $7$ pelo Método de Newton, primeiramente precisamos montar a função $f(x)$ e em seguida encontrar sua derivada:
\begin{equation*}
f(x) = x^2-7\\
f^\prime (x) = 2x
\end{equation*}
Primeiramente montamos a função $f(x)$:
\begin{equation*}
f(x) = x^3+3x^2-4x+1\\
f^\prime (x) = 3x^2 + 6x - 4
\end{equation*}
\begin{equation*}
1.564.000 = 1.000.000 e^x + \frac{435.000}{x} \left(e^x - 1 \right)
\end{equation*}
Primeiramente montamos a função $f(x)$ e em seguida encontrar sua derivada:
\begin{equation*}
f(x) = 1000000 e^x + \frac{435000}{x}\left(e^x-1\right)\\
f^\prime (x) = 1000000e^x + \frac{435000}{x} e^x - \frac{435000}{x^2} \left(e^x - 1\right)
\end{equation*}
Primeiramente vamos montar o sistema de equações:
\begin{equation*}
\left\{\begin{matrix}
x+y = 20\\
\left(x+\sqrt{x} \right )\left(y+\sqrt{y} \right ) = 155,55
\end{matrix}\right.
\\
\left\{\begin{matrix}
x = 20-y\\
\left(x+\sqrt{x} \right )\left(y+\sqrt{y} \right ) = 155,55
\end{matrix}\right.
\end{equation*}
A função será:
\begin{equation*}
f(x)= \left(x+\sqrt{x}\right) \left(20-x+\sqrt{20-x}\right)-155,55
\end{equation*}
E sua derivada será:
\begin{equation*}
f^\prime (x) = \left( 1+\frac{1}{2\sqrt{x}}\right) \left(20-x+\sqrt{20-x}\right) + \left(x+\sqrt{x}\right) \left(-1-\frac{1}{2\sqrt{20-x}}\right)
\end{equation*}
Após encontrarmos o valor de $x$, substituirmos em uma das equações do sistema para encontrarmos o valor de $y$.
\begin{equation*}
A=\frac{P}{i} \left[ (1+i)^n - 1\right]
\end{equation*}
Nesta equação, $A$ é o montante da conta, $P$ é o valor regularmente depositado e $i$ é a taxa de juros por período para os $n$ períodos em que os depósitos foram efetuados. Um engenheiro gostaria de ter em sua conta um total de $\text{R}\$750.000,00$ para efetuar retiradas após $20$ anos e poder dispor de $\text{R}\$1.500,00$ por mês para atingir essa meta. Qual a taxa de juros mínima a que esse valor deve ser investido, assumindo que o período de capitalização é mensal?
\begin{equation*}
A=750.000\\
P=1.500\\
n=240 \: \text{meses}
\end{equation*}
Montamos, então, a função $f(i)$ e em seguida encontramos sua derivada:
\begin{equation*}
f(i) = \frac{1500}{i} \left[ (1+i)^{240}-1\right] - 750000
\end{equation*}
\begin{equation*}
f^{\prime}(i) = \frac{360000(1+i)^{239}}{i} - \frac{1500\left[ (1+i)^{240}-1\right]}{i^2}
\end{equation*}
\begin{equation*}
A=\frac{P}{i}\left[1-(1+i)^{-n}\right]
\end{equation*}
conhecida como equação da anuidade ordinária. Nesta equação $A$ é o total da hipoteca, $P$ é o valor de cada pagamento e $i$ é a taxa de juros por período para $n$ períodos de pagamento. Suponha que seja necessário fazer uma hipoteca de uma casa por um período de $30$ anos no valor de $\text{R}\$135.000,00$ e o tomador do empréstimo possa dispor de no máximo $\text{R}\$1.000,00$ por mês. Qual a taxa máxima de juros que o tomador do empréstimo pode pagar?
\begin{equation*}
A=135000\\
P=1000\\
n=360 \: \text{meses}
\end{equation*}
Montamos a função $f(i)$ e em seguida encontramos sua derivada:
\begin{equation*}
f(i) = \frac{1000}{i} \left[1-(1+i)^{-360}\right] -135000
\end{equation*}
\begin{equation*}
f^{\prime}(i)=\frac{360000}{i(1+i)^{361}} - \frac{1000\left[1-\frac{1}{(1+i)^{360}}\right]}{i^2}
\end{equation*}
Clique aqui e faça o download dos exercícios resolvidos no Excel.
Método de Herão para Aproximação de Raiz Quadrada de um Número n
Método Babilônico para Aproximação de Raiz Quadrada de um Número n

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
Matemática
Zeros Reais de Funções Reais – O Método de Newton Raphson Resolvido no Excel
Introdução:
Sabemos que para alguns tipos de funções existem fórmulas fechadas que levam às raízes em função dos coeficientes, como por exemplo, as equações polinomiais de segundo grau. No entanto, no caso de um polinômio de grau mais alto e de funções mais complicadas, fica praticamente impossível localizar suas raízes.De modo a contornar este problema, foram criados métodos iterativos de aproximações de raízes de funções com qualquer precisão pré-fixada.
Inicialmente, temos que encontrar um intervalo $I=[a,b]$ cuja raiz está contida. Para tal, devemos fazer uma análise teórica da função. Podemos utilizar o seguinte teorema:
Teorema $1$:
Seja uma função $f(x)$ contínua num intervalo $I=[a,b]$. Se $f(a) \cdot f(b) < 0$, então existe pelo menos uma raiz de $f(x)$ neste intervalo.
Dada a função $f(x)=x \log (x) - 1$, podemos construir uma tabela com vários valores para $x$ e analisar as mudanças de sinal de $f(x)$, encontrando um intervalo $I=[a,b]$:

Podemos obter, a partir de uma função $f(x)$, uma função equivalente $g(x)=h(x)$, onde, ao analisarmos graficamente as duas funções, localizamos o ponto de intersecção entre as duas curvas e, assim, o intervalo $I$ que contém a raiz, sem precisar calcular $f(x)$.
Exemplo $1$:
Dada a função $f(x)=4 \cos (x) - 2^{2x}$. Podemos reescrevê-la como $4 \cos(x) = e^{2x}$. Temos então:\begin{equation*}
g(x) = 4 \cos (x) \quad \text{e} \quad h(x) = e^{2x}
\end{equation*}
Graficamente temos:

$\xi _1$ está no intervalo $I_1=[0, \pi]$;
$\xi_2$ está no intervalo $I_2=[-\pi, 0]$, para $k=1$;
$\xi_3$ está no intervalo $I_3=[-2\pi, -pi]$, para $k=2$;
$\xi_4$ está no intervalo $I_4=[-3\pi, -2\pi]$, para $k=2$.
Logo, as raízes são: $[0, \pi] \cup [-(k+1)\pi, 0 -k\pi], k \in \mathbb{Z}^+$.
Exemplo $2$:
Dada a função $f(x)=x^3-9x+3$, obtemos a função equivalente $g(x)=h(x)$:\begin{equation*}
g(x)=x^3 \quad \text{e} \quad h(x)=9x-3
\end{equation*}
Graficamente temos:

Notamos que as raízes:
$\xi_1$ está no intervalo $I_1=[-2,-1]$;
$\xi_2$ está no intervalo $I_2=[0,1]$;
$\xi_3$ está no intervalo $I_3=[1,2]$.
Vejam que desta forma encontramos os intervalos onde contém pelo menos uma raiz.
Existem métodos para aproximar raízes reais de funções reais, tais como o Método da Bissecção, Método da Posição Falsa, Método do Ponto Fixo; Método da Secante e Método de Newton-Raphson. Vamos estudar a seguir o Método de Newton-Raphson.
Método de Newton-Raphson
Seja $f \in \mathcal{C}^2 [a,b]$ (conjunto das funções deriváveis até a segunda derivada no intervalo $[a,b]$), $\in [a,b]$, $f(p)=0$, onde $\overline{x}$ é a aproximação de $p$ ral que $f^\prime (\overline{x})\neq 0$ e $|p-x| < \varepsilon$, com $\varepsilon \in \mathbb{R}$, suficientemente pequeno.\begin{equation*}
f(x)=f(\overline{x})=f^\prime (\overline{x})(x-\overline{x})+f^{\prime \prime}(\xi (x))\cdot \frac{(x-\overline{x})^2}{2}
\end{equation*}
Se $x=p$:
\begin{equation*}
f(p)=f(\overline{x})=f^\prime (\overline{x})(p-\overline{x})+f^{\prime \prime}(\xi (p))\cdot \frac{(p-\overline{x})^2}{2}
\end{equation*}
Como $|p-\overline{x}| < \varepsilon$, e $\varepsilon$ é suficientemente pequeno, seu quadrado será ainda menor e tenderá a zero. Logo:
\begin{equation*}
f(p)=f(\overline{x}) + f^\prime(\overline{x})(p-\overline{x})\\
0=f(\overline{x})+ f^\prime(\overline{x})(p-\overline{x})
\end{equation*}
Que é a equação da reta tangente a $f(x)$ no ponto $\overline{x}$.
Isolando $p$:
\begin{equation*}
p=\overline{x} - \frac{f(\overline{x})}{f^\prime (\overline{x})}
\end{equation*}
Que nos leva ao algoritmo de Newton:
\begin{equation*}
x_{k+1}=x_k - \frac{f(x_k)}{f^\prime(x_k)}
\end{equation*}
Observação: Seja a função $f(x)=x^2$, sua derivada será $f^\prime(x)=2x$. Qual é a equação da reta tangente no ponto igual a $4$?
\begin{equation*}
T(x)=f(\overline{x}) + f^\prime (\overline{x})(x-\overline{x})\\
T(x) = f(4) + f^\prime (4)(x-4)\\
T(x) = 16 + 8(x-4)
\end{equation*}
onde $T(x)$ é a tangente no ponto.
Graficamente temos:

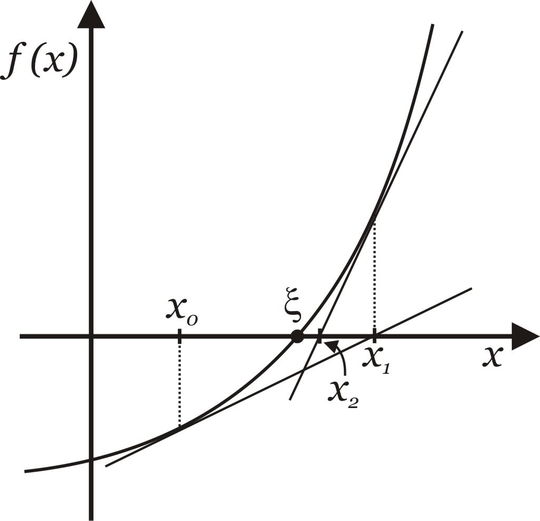
Interpretação geométrica do Método de Newton

Vejam que a cada iteração a raiz se aproxima mais da raiz real $\xi$.
Exemplo $3$:
Seja $f(x)=x^2-6$. Utilizando o método de Newton, obtenha uma aproximação da raiz positiva de $f(x)$. Determine $k_3$.\begin{equation*}
f(x)=x^2-6\
x^2-6=0\\
x^2=6\\
x=\sqrt{6}
\end{equation*}
Então, se $f(x)=x^2-6$ sua derivada será $f^\prime(x)=2x$.
Como a raiz quadrada de $6$ está localizada entre $2$ e $3$, podemos adotar um valor inical entre este intervalo ou em sua proximidade. Vamos adotar $1$ como valor inicial.
\begin{equation*}
x_{k+1} = x_k - \frac{f(x_k)}{f^\prime(x_k)}
\end{equation*}
Para $k_0 = 1$, temos:
\begin{equation*}
x_1 = x_0 - \frac{f(x_0)}{f^\prime(x_0)} = 1 - \frac{f(1)}{f^\prime (1)} = 1-\frac{5}{2} = 3,5
\end{equation*}
Para $k_1=3,5$, temos:
\begin{equation*}
x_2 = x_1 - \frac{f(x_1)}{f^\prime(x_1)} = 3,5 - \frac{f(3,5)}{f^\prime (3,5)} = 3,5 - \frac{6,25}{7} = 2,60714
\end{equation*}
Para $k_2=2,60714$, temos:
\begin{equation*}
x_3=x_2 - \frac{f(x_2)}{f^\prime(x_2)} = 2,60714 - \frac{f(2,60714)}{f^\prime (2,60714)} = 2,60714 - \frac{0,797178}{5,21418} = 2,45425638
\end{equation*}
Para $k_3 = 2,45425638$, temos:
\begin{equation*}
x_4 = x_3 - \frac{f(x_3)}{f^\prime(x_3)} = 2,45425638 - \frac{f(2,45425638)}{f^\prime (2,45425638)} = 2,45425638 - \frac{0,023374378}{4,90851276} = 2,449494413
\end{equation*}
Tomamos então $x_4$ como raiz aproximada de $f(x)$. E se fizermos a raiz quadrada de $6$ pela calculadora, notaremos que a raiz aproximada está correta até a quarta casa decimal.
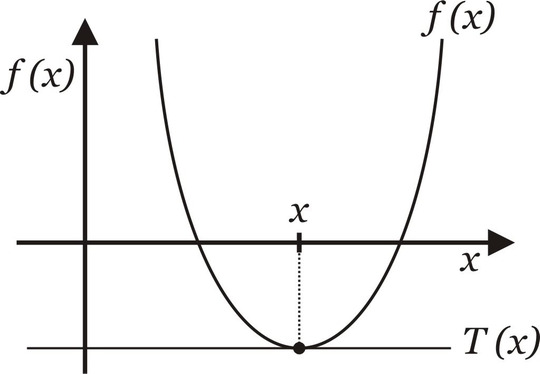
Quando o Método de Newton pode não convergir?
A não convergência do método pode ocorrer nos pontos de máximos, mínimos e inflexão, quando a função muda a concavidade.Isso é fácil de verificar: sabemos que a derivada de uma função num ponto $x$ é a reta tangente À função neste ponto. Se o ponto $x$ é o ponto de mínimo, por exemplo, de uma função quadrática, a reta tangente $T(x)$ neste ponto será paralela ao eixo dos $x$.

Se analisarmos o algoritmo de Newton, veremos que o quociente entre a função e sua derivada será uma indeterminação, tendendo ao infinito.
\begin{equation*}
x_{k+1} = x_k - \frac{f(x_k)}{f^\prime (x_k)}
\end{equation*}
Critérios de parada
Devido ao método de Newton utilizar uma função de iteração $f(x)$, devemos impor alguma condição para que essas iterações parem, ou os cálculos se estenderão ao infinito.Para isso, devemos impor uma precisão inicial $\varepsilon$ para a raiz aproximada da função, tal que, se $f(x_k) < \varepsilon$, então para com as iterações e tome $\overline{x}$ como raiz aproximada de $f(x)$.
Algoritmo
Pensando em escrever um algoritmo em qualquer linguagem de programação, ou mesmo no Excel, podemos seguir as etapas como descritas abaixo:Seja $f(x)=0$ e sejam $f(x)$, $f^\prime (x)$ e $f^{\prime \prime}(x)$ contínuas num intervalo $I$ contendo a raiz $x=\xi$ de $f(x)=0$ e $f(\xi) \neq 0$.
Etapa $1$:
Dados iniciais:$a)$ $x_0$: Aproximação inicial;
$b)$ $\varepsilon _1$ e $\varepsilon _2$ precisões.
Etapa $2$:
Se $|f(x_0)| < \varepsilon_1$, então faça $\overline{x} = x_0$.Fim
Senão:
Etapa $3$:
$k=1$
Etapa $4$:
$\displaystyle x_1 = x_0 - \frac{f(x_0)}{f^\prime (x_0)}$Etapa $5$:
Se $|f(x_0) | < \varepsilon _1$ ou $|x_1-x_0| < \varepsilon _2$, faça $\overline{x} = x_1$Fim
Senão:
Etapa $6$:
$x_0 = x_1$Etapa $7$:
$k = k+1$Volte à etapa $4$
Conclusão
O método ideal para aproximação de raízes é aquele que a convergência é assegurada, e rápida, e que haja um número mínimo de iterações. Dentre os métodos, o Método de Newton é o mais indicado sempre que for fácil verificar as condições de convergência de $f(x)$ e que o cálculo de sua derivada não seja muito elaborado.
Exercício $1$
Encontrar a raiz de $7$ pelo Método de Newton.Para encontrarmos a raiz quadrada de $7$ pelo Método de Newton, primeiramente precisamos montar a função $f(x)$ e em seguida encontrar sua derivada:
\begin{equation*}
f(x) = x^2-7\\
f^\prime (x) = 2x
\end{equation*}
Exercício $2$
Encontrar pelo menos uma raiz real para a cúbica $x^3+3x^2-4x+1$.Primeiramente montamos a função $f(x)$:
\begin{equation*}
f(x) = x^3+3x^2-4x+1\\
f^\prime (x) = 3x^2 + 6x - 4
\end{equation*}
Exercício $3$
Encontrar um valor aproximado para $x$ com precisão de $10^{-8}$ para a equação da população:\begin{equation*}
1.564.000 = 1.000.000 e^x + \frac{435.000}{x} \left(e^x - 1 \right)
\end{equation*}
Primeiramente montamos a função $f(x)$ e em seguida encontrar sua derivada:
\begin{equation*}
f(x) = 1000000 e^x + \frac{435000}{x}\left(e^x-1\right)\\
f^\prime (x) = 1000000e^x + \frac{435000}{x} e^x - \frac{435000}{x^2} \left(e^x - 1\right)
\end{equation*}
Exercício $4$
A soma de dois números é $20$. Se a cada número é adicionado de sua raiz quadrada, o produto das duas somas é $155,55$. Determine os dois números com precisão de $\varepsilon = 10^{-4}$.Primeiramente vamos montar o sistema de equações:
\begin{equation*}
\left\{\begin{matrix}
x+y = 20\\
\left(x+\sqrt{x} \right )\left(y+\sqrt{y} \right ) = 155,55
\end{matrix}\right.
\\
\left\{\begin{matrix}
x = 20-y\\
\left(x+\sqrt{x} \right )\left(y+\sqrt{y} \right ) = 155,55
\end{matrix}\right.
\end{equation*}
A função será:
\begin{equation*}
f(x)= \left(x+\sqrt{x}\right) \left(20-x+\sqrt{20-x}\right)-155,55
\end{equation*}
E sua derivada será:
\begin{equation*}
f^\prime (x) = \left( 1+\frac{1}{2\sqrt{x}}\right) \left(20-x+\sqrt{20-x}\right) + \left(x+\sqrt{x}\right) \left(-1-\frac{1}{2\sqrt{20-x}}\right)
\end{equation*}
Após encontrarmos o valor de $x$, substituirmos em uma das equações do sistema para encontrarmos o valor de $y$.
Exercício $5$
O montante acumulado de uma conta de poupança baseada em depósitos regulares periódicos pode ser determinado a partir da equação de anuidades devidas:\begin{equation*}
A=\frac{P}{i} \left[ (1+i)^n - 1\right]
\end{equation*}
Nesta equação, $A$ é o montante da conta, $P$ é o valor regularmente depositado e $i$ é a taxa de juros por período para os $n$ períodos em que os depósitos foram efetuados. Um engenheiro gostaria de ter em sua conta um total de $\text{R}\$750.000,00$ para efetuar retiradas após $20$ anos e poder dispor de $\text{R}\$1.500,00$ por mês para atingir essa meta. Qual a taxa de juros mínima a que esse valor deve ser investido, assumindo que o período de capitalização é mensal?
\begin{equation*}
A=750.000\\
P=1.500\\
n=240 \: \text{meses}
\end{equation*}
Montamos, então, a função $f(i)$ e em seguida encontramos sua derivada:
\begin{equation*}
f(i) = \frac{1500}{i} \left[ (1+i)^{240}-1\right] - 750000
\end{equation*}
\begin{equation*}
f^{\prime}(i) = \frac{360000(1+i)^{239}}{i} - \frac{1500\left[ (1+i)^{240}-1\right]}{i^2}
\end{equation*}
Exercício $6$
Problemas que envolvem a quantia necessária para pagar uma hipoteca por um período fixo de tempo utilizam a fórmula:\begin{equation*}
A=\frac{P}{i}\left[1-(1+i)^{-n}\right]
\end{equation*}
conhecida como equação da anuidade ordinária. Nesta equação $A$ é o total da hipoteca, $P$ é o valor de cada pagamento e $i$ é a taxa de juros por período para $n$ períodos de pagamento. Suponha que seja necessário fazer uma hipoteca de uma casa por um período de $30$ anos no valor de $\text{R}\$135.000,00$ e o tomador do empréstimo possa dispor de no máximo $\text{R}\$1.000,00$ por mês. Qual a taxa máxima de juros que o tomador do empréstimo pode pagar?
\begin{equation*}
A=135000\\
P=1000\\
n=360 \: \text{meses}
\end{equation*}
Montamos a função $f(i)$ e em seguida encontramos sua derivada:
\begin{equation*}
f(i) = \frac{1000}{i} \left[1-(1+i)^{-360}\right] -135000
\end{equation*}
\begin{equation*}
f^{\prime}(i)=\frac{360000}{i(1+i)^{361}} - \frac{1000\left[1-\frac{1}{(1+i)^{360}}\right]}{i^2}
\end{equation*}
Clique aqui e faça o download dos exercícios resolvidos no Excel.
Veja mais:
Método de Newton para Aproximação de Raiz Quadrada de um Número nMétodo de Herão para Aproximação de Raiz Quadrada de um Número n
Método Babilônico para Aproximação de Raiz Quadrada de um Número n

- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
