Matemática
O bom entendimento sobre as medidas de ângulos em graus e em radianos é necessário para o estudo da circunferência trigonométrica para que possamos também trabalhar com ângulos que não sejam agudos e fazer um estudo mais geral e completo, preparando-se para o estudo das funções trigonométricas.
Acredita-se que os sumérios e os arcadinos $(3500a.C.)$ já sabiam medir ângulos.
Um dos primeiros astrônomos gregos a dividir o círculo em $360$ partes iguais foi Hipsicles (século $IIIa.C.$), talvez por acreditarem que a Terra leva cerca de $360$dias para completar sua translação em torno do Sol. Mas a hipótese mais provável é ter havido influência do sistema de numeração sexagesimal (base $60$), utilizado na Babilônia.
Se pudermos retificar essa circunferência, ou seja, transformá-la em um segmento de reta, este segmento teria o comprimento $C$ que seria o comprimento da própria circunferência. Veja aqui um exemplo de retificação da circunferência.
O comprimento $C$ da circunferência é dado por:
\begin{equation}
C=2\pi r
\end{equation}
onde $r$ é o raio da circunferência e $\pi$ é uma constante irracional, presente em toda circunferência e numericamente vale $3,1415$, aproximadamente. Veja aqui uma breve cronologia de $\pi$.
No caso de uma régua, existem versões com escalas em milímetros, outras em centímetros. As trenas possuem marcação de milímetros, centímetros e metros. Já o odômetro de um veículo, mede com precisão de $100$ metros.
Então, medida é a razão entre duas grandezas de mesma espécie.
Sendo assim, a medida de um arco de circunferência $\widehat{AB}$ é um número $\alpha$, não-negativo, determinado pela razão entre o arco $\widehat{AB}$ a ser medido e um arco unitário $u$ da mesma circunferência. Simbolicamente temos:
\begin{equation}
\alpha = \frac{\widehat{AB}}{u}
\end{equation}
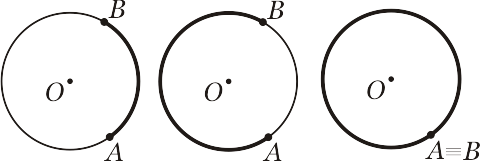
Se os pontos coincidem, teremos arco nulo ou arco de uma volta.
Em problemas de nosso cotidiano, minutos e segundos de grau não são muito utilizados, mas em medições técnicas e em astronomia, seu uso é essencial. Assim:
\begin{equation}
1º = 60^\prime \Rightarrow 1^\prime = 60^{\prime \prime} \Rightarrow 1º = 3600^{\prime \prime}
\end{equation}
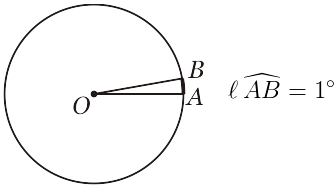
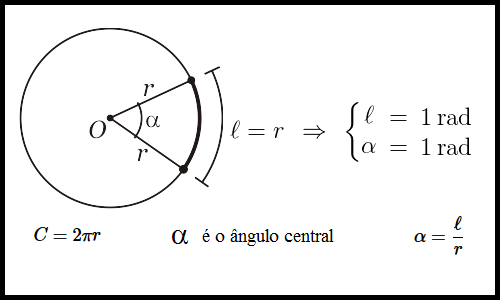
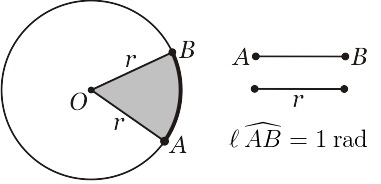
Dizemos que um arco mede $1$ radiano $(1\:\text{rad})$ se o seu comprimento $\ell$ for igual ao comprimento do raio $r$. Assim, a medida do ângulo central também será de $1$ radiano.
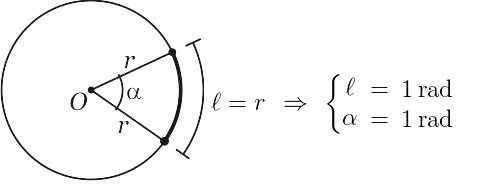
Então, para sabermos a medida de um arco ou ângulo central correspondente, em radianos, calculamos quantas vezes esse arco de comprimento $\ell$ contém a medida do raio $r$. Obtemos dividindo $\ell$ por $r$:
\begin{equation}
\alpha = \frac{\ell}{r}
\end{equation}
Se $\ell$ é o arco de uma volta, então $\ell$ é o comprimento da circunferência $C=2\pi r$:
\begin{equation}
\alpha = \frac{\ell}{r} = \frac{2 \pi r}{r} = 2\pi \: \text{rad}
\end{equation}
Assim, a circunferência é um arco de $2\pi \: \text{rad}$ e o ângulo central de uma volta mede $2\pi \: \text{rad}$. E como o ângulo de uma volta tem $360º$, então $2\pi \: \text{rad}$ equivale a $360º$.
\begin{equation}
\ell = \alpha \cdot r
\end{equation}
onde $\ell$ é o comprimento do arco, $r$ é o raio e $\alpha$ é a medida do ângulo central em radianos.
Resolução: Como o diâmetro é de $50m$, o raio mede $25m$ e o comprimento da pista é:
\begin{equation*}
C=2\pi r=2\pi \cdot 25=50\pi \cong 157m
\end{equation*}
Como foram $6$ voltas, basta multiplicarmos o resultado obtido por $6$. A distância percorrida foi de $157\cdot 6=942$.
$2)$ Converter as medidas de ângulos:
$a)$ $270º$ em radianos
Como $360º=2\pi \: \text{rad}$, então $180º=\pi \: \text{rad}$. Usamos este valor como referência na regade três:
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
x & = & 270º
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{3}{2} \pi \: \text{rad}$
$b)$ $2/3 \pi \: \text{rad}$ em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
2/3 \pi \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $x=120º$
$c)$ $37º30^\prime$ em radianos
Primeiro convertemos $37º30^\prime$ em segundos de grau:
\begin{equation*}
37º30^\prime = 37 \cdot 60^\prime + 30^\prime = 2250^\prime
\end{equation*}
E agora convertemos $180º$ em minutos de grau, obtendo $10800^\prime$.
Então fazemos:
\begin{matrix}
10800^\prime& = & \pi \: \text{rad}\\
2250^\prime & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{5}{24} \pi \: \text{rad}$
$d)$ $\pi/16 \: \text{rad}$ em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
\pi/16 \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{180º}{16}=11,25º$. Podemos escrever:
\begin{equation*}
x=11,25º = 11º + 0,25\cdot 60^\prime=11º15^\prime
\end{equation*}
$e)$ $1$ radiano em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
1 \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{180º}{\pi}\cong 57,2957795º$, ou $x\cong 57º19^\prime 29^{\prime \prime}$
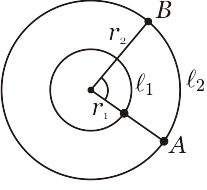
$3)$ As circunferências da figura abaixo são concêntricas, sendo $r_1=3\:cm$, $r_2=8\: cm$ e $\ell_2=40\: cm$. Calcular: $a)$ o ângulo $\alpha$ em radianos e $b)$ o arco $\ell_1$.
Resolução:
$a)$ $\displaystyle \alpha = \frac{\ell_2}{r_2}=\frac{40}{8}=5\: \text{rad}$
$b)$$\displaystyle \alpha = \frac{\ell_1}{r_1} \Rightarrow s_1=\alpha r_1=5\cdot 3= 15\:cm$
[2] Matemática V. Único - Marcondes, Gentil & Sérgio
[3] Matemática V. 2 Contextos e Aplicações - Dante
➋ A Astronomia e os Astrônomos da Grécia Antiga
➌ Como Encontrar o Centro de uma Circunferência

- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Teorema Do Quadrilátero Inscritível
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência. Teorema: Se um quadrilátero é inscritível numa circunferência, então os ângulos opostos são suplementares. Por hipóteses temos que o quadrilátero...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
Matemática
Arcos de Circunferência
O bom entendimento sobre as medidas de ângulos em graus e em radianos é necessário para o estudo da circunferência trigonométrica para que possamos também trabalhar com ângulos que não sejam agudos e fazer um estudo mais geral e completo, preparando-se para o estudo das funções trigonométricas.

Introdução
Os ângulos aparecem nos registros da Grécia antiga associados ao estudo dos elementos de uma círculo, relacionados com arcos e cordas. As propriedades do ângulo central de uma circunferência eram conhecidas desde os tempo de Eudoxo (Astrônomo, matemático e filósofo grego do século $IVa.C.$), que teria usado medidas de ângulos em diversos cálculos, como a determinação das dimensões da Terra e a distância relativa entre o Sol e a Terra.Acredita-se que os sumérios e os arcadinos $(3500a.C.)$ já sabiam medir ângulos.
Um dos primeiros astrônomos gregos a dividir o círculo em $360$ partes iguais foi Hipsicles (século $IIIa.C.$), talvez por acreditarem que a Terra leva cerca de $360$dias para completar sua translação em torno do Sol. Mas a hipótese mais provável é ter havido influência do sistema de numeração sexagesimal (base $60$), utilizado na Babilônia.
Comprimento de uma circunferência
Seja um círculo qualquer de centro $O$ e raio $r$. A borda desse círculo, ou seja, o contorno desse círculo é chamado de circunferência.Se pudermos retificar essa circunferência, ou seja, transformá-la em um segmento de reta, este segmento teria o comprimento $C$ que seria o comprimento da própria circunferência. Veja aqui um exemplo de retificação da circunferência.
O comprimento $C$ da circunferência é dado por:
\begin{equation}
C=2\pi r
\end{equation}
onde $r$ é o raio da circunferência e $\pi$ é uma constante irracional, presente em toda circunferência e numericamente vale $3,1415$, aproximadamente. Veja aqui uma breve cronologia de $\pi$.
Medidas de arcos e ângulos
Sempre que quisermos medir alguma grandeza, usamos outra grandeza padrão como uma medida unitária e depois procuramos descobrir quantas vezes a grandeza a ser medida contém a grandeza padrão.No caso de uma régua, existem versões com escalas em milímetros, outras em centímetros. As trenas possuem marcação de milímetros, centímetros e metros. Já o odômetro de um veículo, mede com precisão de $100$ metros.
Então, medida é a razão entre duas grandezas de mesma espécie.
Sendo assim, a medida de um arco de circunferência $\widehat{AB}$ é um número $\alpha$, não-negativo, determinado pela razão entre o arco $\widehat{AB}$ a ser medido e um arco unitário $u$ da mesma circunferência. Simbolicamente temos:
\begin{equation}
\alpha = \frac{\widehat{AB}}{u}
\end{equation}
Definição $1$: Arco de circunferência
Arco de circunferência é cada uma das duas partes em que uma circunferência fica dividida por dois pontos. assim, sendo $A$ e $B$ dois de seus pontos, eles a dividem em duas partes:
Se os pontos coincidem, teremos arco nulo ou arco de uma volta.
Grau
Foi convencionada a divisão da circunferência em $360$ arcos congruentes. Cada um desses arcos foi chamado de arco de um grau $(1º)$. Cada arco de $1º$ foi dividido em $60$ sub-arcos congruentes e cada um desses sub-arcos recebeu o nome de minuto de grau $(1^\prime)$. E cada arco de minuto de grau foi sub-dividido em outros $60$ arcos congruentes dando origem ao arco de segundo de grau $(1^{\prime \prime}$). Um exemplo dessa notação é $30º 12^\prime 15^{\prime \prime}$.Em problemas de nosso cotidiano, minutos e segundos de grau não são muito utilizados, mas em medições técnicas e em astronomia, seu uso é essencial. Assim:
\begin{equation}
1º = 60^\prime \Rightarrow 1^\prime = 60^{\prime \prime} \Rightarrow 1º = 3600^{\prime \prime}
\end{equation}
Definição $2$: Grau
Grau é o arco unitário equivalente a $1/360$ da circunferência que o contém:Radiano
Seja uma circunferência de centro $O$ e raio $r$ e seja $\ell$ o comprimento de um arco de circunferência com medida de ângulo central igual a $\alpha$.Dizemos que um arco mede $1$ radiano $(1\:\text{rad})$ se o seu comprimento $\ell$ for igual ao comprimento do raio $r$. Assim, a medida do ângulo central também será de $1$ radiano.
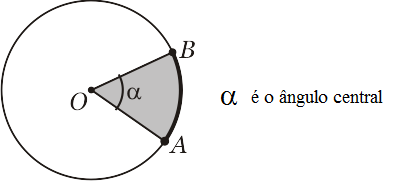
Definição $3$: Ângulo central
Ângulo central de uma circunferência é o ângulo que tem o vértice no centro $O$ da circunferência.Então, para sabermos a medida de um arco ou ângulo central correspondente, em radianos, calculamos quantas vezes esse arco de comprimento $\ell$ contém a medida do raio $r$. Obtemos dividindo $\ell$ por $r$:
\begin{equation}
\alpha = \frac{\ell}{r}
\end{equation}
Se $\ell$ é o arco de uma volta, então $\ell$ é o comprimento da circunferência $C=2\pi r$:
\begin{equation}
\alpha = \frac{\ell}{r} = \frac{2 \pi r}{r} = 2\pi \: \text{rad}
\end{equation}
Assim, a circunferência é um arco de $2\pi \: \text{rad}$ e o ângulo central de uma volta mede $2\pi \: \text{rad}$. E como o ângulo de uma volta tem $360º$, então $2\pi \: \text{rad}$ equivale a $360º$.
Definição $4$: Radiano
Radiano é o arco cujo comprimento é igual ao comprimento do raio da circunferência que o contém.Comprimento de uma arco de circunferência
Seja uma circunferência de centro $O$ e raio $r$, cujo ângulo central de um arco de comprimento $\ell$ corresponde em radianos mede $\alpha$. Da relação $(4)$ concluímos que:\begin{equation}
\ell = \alpha \cdot r
\end{equation}
onde $\ell$ é o comprimento do arco, $r$ é o raio e $\alpha$ é a medida do ângulo central em radianos.
Exemplos
$1)$ Uma pista circular de atletismo tem diâmetro de $50m$. Calcular a distância percorrida por um atleta após dar $6$ voltas completas nesta pista.Resolução: Como o diâmetro é de $50m$, o raio mede $25m$ e o comprimento da pista é:
\begin{equation*}
C=2\pi r=2\pi \cdot 25=50\pi \cong 157m
\end{equation*}
Como foram $6$ voltas, basta multiplicarmos o resultado obtido por $6$. A distância percorrida foi de $157\cdot 6=942$.
$2)$ Converter as medidas de ângulos:
$a)$ $270º$ em radianos
Como $360º=2\pi \: \text{rad}$, então $180º=\pi \: \text{rad}$. Usamos este valor como referência na regade três:
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
x & = & 270º
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{3}{2} \pi \: \text{rad}$
$b)$ $2/3 \pi \: \text{rad}$ em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
2/3 \pi \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $x=120º$
$c)$ $37º30^\prime$ em radianos
Primeiro convertemos $37º30^\prime$ em segundos de grau:
\begin{equation*}
37º30^\prime = 37 \cdot 60^\prime + 30^\prime = 2250^\prime
\end{equation*}
E agora convertemos $180º$ em minutos de grau, obtendo $10800^\prime$.
Então fazemos:
\begin{matrix}
10800^\prime& = & \pi \: \text{rad}\\
2250^\prime & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{5}{24} \pi \: \text{rad}$
$d)$ $\pi/16 \: \text{rad}$ em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
\pi/16 \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{180º}{16}=11,25º$. Podemos escrever:
\begin{equation*}
x=11,25º = 11º + 0,25\cdot 60^\prime=11º15^\prime
\end{equation*}
$e)$ $1$ radiano em graus
\begin{matrix}
\pi \: \text{rad}& = & 180º\\
1 \: \text{rad} & = &x
\end{matrix}
Resolvendo, encontramos $\displaystyle x=\frac{180º}{\pi}\cong 57,2957795º$, ou $x\cong 57º19^\prime 29^{\prime \prime}$
$3)$ As circunferências da figura abaixo são concêntricas, sendo $r_1=3\:cm$, $r_2=8\: cm$ e $\ell_2=40\: cm$. Calcular: $a)$ o ângulo $\alpha$ em radianos e $b)$ o arco $\ell_1$.
Resolução:
$a)$ $\displaystyle \alpha = \frac{\ell_2}{r_2}=\frac{40}{8}=5\: \text{rad}$
$b)$$\displaystyle \alpha = \frac{\ell_1}{r_1} \Rightarrow s_1=\alpha r_1=5\cdot 3= 15\:cm$
Referências
[1] Matemática V. Único - Facchini[2] Matemática V. Único - Marcondes, Gentil & Sérgio
[3] Matemática V. 2 Contextos e Aplicações - Dante
Vejam mais:
➊ O Surgimento do Grau na Circunferência➋ A Astronomia e os Astrônomos da Grécia Antiga
➌ Como Encontrar o Centro de uma Circunferência

- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Teorema Do Quadrilátero Inscritível
Um quadrilátero está inscrito numa circunferência se seus vértices são pontos desta circunferência. Teorema: Se um quadrilátero é inscritível numa circunferência, então os ângulos opostos são suplementares. Por hipóteses temos que o quadrilátero...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
- Ângulo De Segmento Ou ângulo Semi-inscrito
Nesta postagem, veremos como determinar o ângulo de segmento e provar que vale a metade do ângulo central. Definição:Ângulo de segmento ou ângulo semi-inscrito relativo a uma circunferência é o ângulo que tem o vértice num ponto da circunferência,...
- Demonstração Da Derivada Da Função Produto
A derivada de uma função pode ser representada geometricamente da seguinte maneira: Se $\Delta x$ for tão pequeno quanto quisermos, a reta que passa pelos pontos $[(x,f(x)),(x+\Delta x, f(x+\Delta x))]$, se confunde com a reta tangente no ponto $x$...
