Matemática
Um polígono é dito regular se tiver todos os seus lados e ângulos iguais, sejam eles internos ou externos.
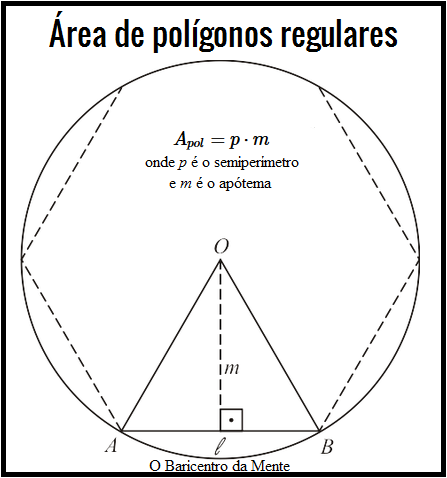
Todo polígono regular pode ser inscrito em uma circunferência, sendo o centro da circunferência, o centro do polígono. Unindo o centro do polígono a cada um de seus vértices, decompomos o polígono em triângulos isósceles.
O segmento que une o centro do polígono ao ponto médio de seus lados é chamado de apótema.
A partir dessas informações, podemos encontrar a fórmula para a área de qualquer polígono regular.
Vamos considerar um polígono regular qualquer:
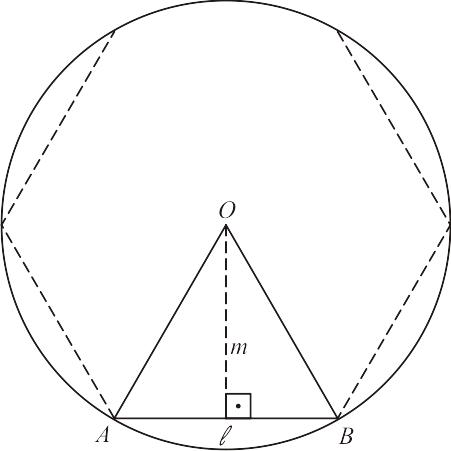
Sejam $\ell$ a medida do lado, $m$ a medida do apótema, $n$ o número de lados do polígono e seja $p$ o semiperímetro .
Podemos decompor um polígono regular em $n$ triângulos de base $\ell$ e altura $m$. Desta forma, a área de cada triângulo será:
\begin{equation}
A_T=\frac{\ell \cdot m}{2}
\end{equation}
e a área do polígono será o produto da área do triângulo $A_T$ pelo número $n$ de lados:
\begin{equation}
A_{pol}=n \cdot A_T = \frac{n \cdot \ell \cdot m}{2}
\end{equation}
No entanto, o semiperímetro $p$ do polígono é dado por:
\begin{equation}
p=\frac{n \cdot \ell}{2}
\end{equation}
Substituindo $(3)$ em $(2)$, obtemos:
\begin{equation}
A_{pol}=\frac{2\cdot p \cdot m}{2}
\end{equation}
Assim, a área de um polígono regular é dado pelo produto entre seu semiperímetro $p$ pelo seu apótema $m$:
\begin{equation}
A_{pol}=p\cdot m
\end{equation}
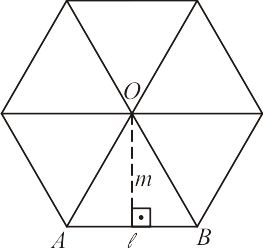
Como o hexágono pode ser dividido em seis triângulos equiláteros, para calcularmos a medida $\ell$ de seus lados, aplicamos o teorema de Pitágoras no triângulo $BOC$:
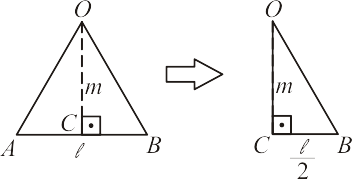
\begin{equation*}
\ell ^2 = \frac{\ell ^2}{4} + m^2\\
\ell^2 - \frac{\ell ^2}{4} = m^2\\
\frac{3\ell ^2}{4} = m^2\\
\ell^2 = \frac{4m^2}{3}\\
\ell = \sqrt{\frac{4m^2}{3}}
\end{equation*}
Substituindo o apótema $m=2\sqrt{3}$:
\begin{equation*}
\ell = \sqrt{\frac{4(2\sqrt{3})^2}{3}}\\
\ell = \sqrt{\frac{4\cdot 4 \cdot 3}{3}}\\
\ell = 4 \:cm
\end{equation*}
Assim, o semiperímetro será:
\begin{equation*}
p=\frac{6\ell}{2} = \frac{6\cdot 4}{2} = 12 \: cm
\end{equation*}
e a área do hexágono será:
\begin{equation*}
A_{pol} = p\cdot m = 12 \cdot 2\sqrt{3}=24\sqrt{3}\approx 41,57\:cm
\end{equation*}
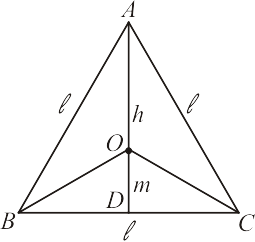
O ponto $O$ é o baricentro do triângulo $\triangle ABC$, de modo que:
\begin{equation*}
m=\frac{1}{3} \overline{DA} = \frac{1}{3} h
\end{equation*}
Sendo o semiperímetro $\displaystyle p=\frac{3\ell}{2}$, temos que:
\begin{equation*}
A_{pol} = p\cdot m = \frac{3\ell}{2} \cdot \frac{1}{3}h = \frac{\ell h}{2}
\end{equation*}
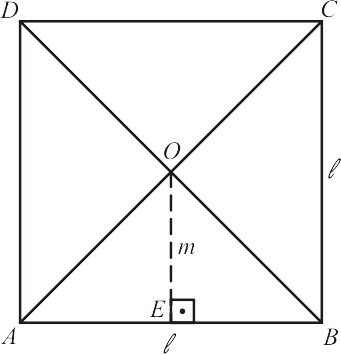
O ponto $O$ é o centro do quadrado $ABCD$ de lados $\ell$. Decompondo em triângulos isósceles, tomamos o triângulo $\triangle AOB$. Assim:
\begin{equation*}
m=\overline{OE} = \frac{\ell}{2}
\end{equation*}
O semiperímetro é $p=2\ell$ e a área do polígono será:
\begin{equation*}
A_{pol}=p\cdot m=2\ell \cdot \frac{\ell}{2}=\ell ^2
\end{equation*}
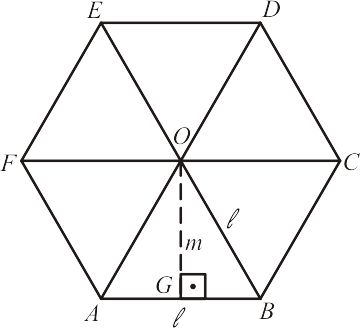
O ponto $O$ é o centro do hexágono $ABCDEF$, por onde o decompomos em seis triângulos equiláteros. Tomando o triângulo $\triangle AOB$ temos que:
\begin{equation*}
m=\overline{OG}=\frac{\ell \sqrt{3}}{2}
\end{equation*}
e o semiperímetro será $p=3\ell$. Assim:
\begin{equation*}
A_{pol} = p\cdot m = 3\ell \cdot \frac{\ell \sqrt{3}}{2} = \frac{3\ell ^2 \sqrt{3}}{2}
\end{equation*}
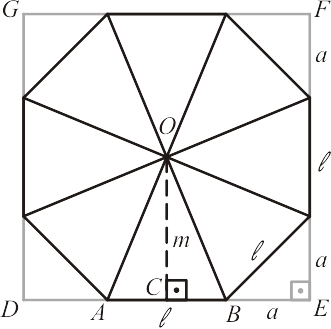
O ponto $O$ é o centro do octógono, por onde o decompomos em $8$ triângulos isósceles. O semiperímetro será $p=4\ell$.
O prolongamento dos lados não adjacentes do octógono forma um quadrado $DEFG$ .Vamos agora escrever os lados dos triângulos formados nos vértices desse quadrado, denotados por $a$, em função do lado $\ell$ do octógono.
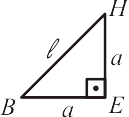
Aplicando o teorema de Pitágoras:
\begin{equation*}
\ell^2 = 2a^2 \Longrightarrow a=\frac{\ell \sqrt{2}}{2}
\end{equation*}
Vejam que $\displaystyle m=\frac{\overline{EF}}{2}$ e $\overline{EF}=\ell +2a$. Assim:
\begin{equation*}
m=\frac{\ell + 2a}{2} = \frac{\ell}{2}+a = \frac{\ell}{2} + \frac{\ell \sqrt{2}}{2} = \frac{\ell (1+\sqrt{2})}{2}
\end{equation*}
A área do octógono será:
\begin{equation*}
A_{pol} = p\cdot m = 4\ell \cdot \frac{\ell(1+\sqrt{2})}{2} = 2\ell^2 (1+\sqrt{2})
\end{equation*}
Apesar de obtermos qualquer área de um polígono regular com a fórmula geral $A_{pol} = p\cdot m$, as deduções acima nos fornecem as áreas dos polígono somente em função de seu lado, o que por vezes pode ser muito mais útil.
Soma dos ângulos internos e externos de um polígono convexo
Como determinar o número de diagonais de um polígono convexo de $N$ lados

- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Área de Polígonos Regulares
Um polígono é dito regular se tiver todos os seus lados e ângulos iguais, sejam eles internos ou externos.

Todo polígono regular pode ser inscrito em uma circunferência, sendo o centro da circunferência, o centro do polígono. Unindo o centro do polígono a cada um de seus vértices, decompomos o polígono em triângulos isósceles.
O segmento que une o centro do polígono ao ponto médio de seus lados é chamado de apótema.
A partir dessas informações, podemos encontrar a fórmula para a área de qualquer polígono regular.
Vamos considerar um polígono regular qualquer:
[Figura 1]
Sejam $\ell$ a medida do lado, $m$ a medida do apótema, $n$ o número de lados do polígono e seja $p$ o semiperímetro .
Podemos decompor um polígono regular em $n$ triângulos de base $\ell$ e altura $m$. Desta forma, a área de cada triângulo será:
\begin{equation}
A_T=\frac{\ell \cdot m}{2}
\end{equation}
e a área do polígono será o produto da área do triângulo $A_T$ pelo número $n$ de lados:
\begin{equation}
A_{pol}=n \cdot A_T = \frac{n \cdot \ell \cdot m}{2}
\end{equation}
No entanto, o semiperímetro $p$ do polígono é dado por:
\begin{equation}
p=\frac{n \cdot \ell}{2}
\end{equation}
Substituindo $(3)$ em $(2)$, obtemos:
\begin{equation}
A_{pol}=\frac{2\cdot p \cdot m}{2}
\end{equation}
Assim, a área de um polígono regular é dado pelo produto entre seu semiperímetro $p$ pelo seu apótema $m$:
\begin{equation}
A_{pol}=p\cdot m
\end{equation}
Exemplo $1$:
Determinar a área de um hexágono cujo apótema mede $\displaystyle 2\sqrt{3} \: cm$.
[Figura 2]
Como o hexágono pode ser dividido em seis triângulos equiláteros, para calcularmos a medida $\ell$ de seus lados, aplicamos o teorema de Pitágoras no triângulo $BOC$:

[Figura 3]
\begin{equation*}
\ell ^2 = \frac{\ell ^2}{4} + m^2\\
\ell^2 - \frac{\ell ^2}{4} = m^2\\
\frac{3\ell ^2}{4} = m^2\\
\ell^2 = \frac{4m^2}{3}\\
\ell = \sqrt{\frac{4m^2}{3}}
\end{equation*}
Substituindo o apótema $m=2\sqrt{3}$:
\begin{equation*}
\ell = \sqrt{\frac{4(2\sqrt{3})^2}{3}}\\
\ell = \sqrt{\frac{4\cdot 4 \cdot 3}{3}}\\
\ell = 4 \:cm
\end{equation*}
Assim, o semiperímetro será:
\begin{equation*}
p=\frac{6\ell}{2} = \frac{6\cdot 4}{2} = 12 \: cm
\end{equation*}
e a área do hexágono será:
\begin{equation*}
A_{pol} = p\cdot m = 12 \cdot 2\sqrt{3}=24\sqrt{3}\approx 41,57\:cm
\end{equation*}
Fórmula para a área de alguns polígonos regulares
A partir da relação $(5)$, podemos determinar a fórmula para a área de alguns polígonos regulares. Veremos apenas alguns, mas o raciocínio segue para os demais.Triângulo equilátero
A área do triângulo é dada pelo semiproduto da base por sua altura: $\displaystyle A_{pol}=\frac{\ell h}{2}$.
[Figura 4]
O ponto $O$ é o baricentro do triângulo $\triangle ABC$, de modo que:
\begin{equation*}
m=\frac{1}{3} \overline{DA} = \frac{1}{3} h
\end{equation*}
Sendo o semiperímetro $\displaystyle p=\frac{3\ell}{2}$, temos que:
\begin{equation*}
A_{pol} = p\cdot m = \frac{3\ell}{2} \cdot \frac{1}{3}h = \frac{\ell h}{2}
\end{equation*}
Quadrado
A área do quadrado é dada pelo produto de dois de seus lados adjacentes: $\displaystyle A_{pol}=\ell^2$.
[Figura 5]
O ponto $O$ é o centro do quadrado $ABCD$ de lados $\ell$. Decompondo em triângulos isósceles, tomamos o triângulo $\triangle AOB$. Assim:
\begin{equation*}
m=\overline{OE} = \frac{\ell}{2}
\end{equation*}
O semiperímetro é $p=2\ell$ e a área do polígono será:
\begin{equation*}
A_{pol}=p\cdot m=2\ell \cdot \frac{\ell}{2}=\ell ^2
\end{equation*}
Hexágono
A área do hexágono é dada por $\displaystyle A_{pol}=\frac{3\ell ^2 \sqrt{3}}{2}$.
[Figura 6]
O ponto $O$ é o centro do hexágono $ABCDEF$, por onde o decompomos em seis triângulos equiláteros. Tomando o triângulo $\triangle AOB$ temos que:
\begin{equation*}
m=\overline{OG}=\frac{\ell \sqrt{3}}{2}
\end{equation*}
e o semiperímetro será $p=3\ell$. Assim:
\begin{equation*}
A_{pol} = p\cdot m = 3\ell \cdot \frac{\ell \sqrt{3}}{2} = \frac{3\ell ^2 \sqrt{3}}{2}
\end{equation*}
Octógono
A área do octógono regular é dada por $\displaystyle 2\ell^2 (1+\sqrt{2})$.
[Figura 7]
O ponto $O$ é o centro do octógono, por onde o decompomos em $8$ triângulos isósceles. O semiperímetro será $p=4\ell$.
O prolongamento dos lados não adjacentes do octógono forma um quadrado $DEFG$ .Vamos agora escrever os lados dos triângulos formados nos vértices desse quadrado, denotados por $a$, em função do lado $\ell$ do octógono.
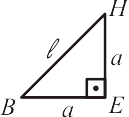
[Figura 8]
Aplicando o teorema de Pitágoras:
\begin{equation*}
\ell^2 = 2a^2 \Longrightarrow a=\frac{\ell \sqrt{2}}{2}
\end{equation*}
Vejam que $\displaystyle m=\frac{\overline{EF}}{2}$ e $\overline{EF}=\ell +2a$. Assim:
\begin{equation*}
m=\frac{\ell + 2a}{2} = \frac{\ell}{2}+a = \frac{\ell}{2} + \frac{\ell \sqrt{2}}{2} = \frac{\ell (1+\sqrt{2})}{2}
\end{equation*}
A área do octógono será:
\begin{equation*}
A_{pol} = p\cdot m = 4\ell \cdot \frac{\ell(1+\sqrt{2})}{2} = 2\ell^2 (1+\sqrt{2})
\end{equation*}
Apesar de obtermos qualquer área de um polígono regular com a fórmula geral $A_{pol} = p\cdot m$, as deduções acima nos fornecem as áreas dos polígono somente em função de seu lado, o que por vezes pode ser muito mais útil.
Referências
[1] Fundamentos de Matemática Elementar V9 - Geometria Plana - Osvaldo Dolce & Nicolau PompeoVeja mais
Como determinar o ângulo interno de um polígono regularSoma dos ângulos internos e externos de um polígono convexo
Como determinar o número de diagonais de um polígono convexo de $N$ lados

- Fórmulas Para A área De Um Triângulo
Veremos neste post $4$ fórmulas para calcular a área de um triângulo. Todas elas dependem de pelo menos um dos lados do triângulo. Primeiramente, determinaremos a área do paralelogramo, que servirá como base para as demonstrações subsequentes....
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
