Matemática
Exemplo 1
Dada a matriz :
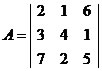, qual o cofator do elemento a12?
Como i = 1 e j = 2, destacamos a 1ª linha e a 2ª coluna de A.
A12 = (-1)³ *
= (-1)*(15-7) = - 8
- O Teorema De Laplace
O Teorema de LaplaceMarcelo Rigonatto DeterminanteO teorema de Laplace consiste num método de calcular o determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator. Lembrando que o cofator do elemento aij de uma matriz...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Menor Complementar
Menor complementar de um elemento de uma matriz é o determinante dela, eliminando a linha e a coluna que pertencer esse elemento. É possível calcular o menor complementar se a matriz for quadrada e de ordem maior ou igual a 2. Dada uma matriz de ordem...
Matemática
Cofator de uma Matriz
Exemplo 1
Dada a matriz :
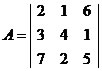, qual o cofator do elemento a12?Como i = 1 e j = 2, destacamos a 1ª linha e a 2ª coluna de A.
A12 = (-1)³ *
= (-1)*(15-7) = - 8
- O Teorema De Laplace
O Teorema de LaplaceMarcelo Rigonatto DeterminanteO teorema de Laplace consiste num método de calcular o determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator. Lembrando que o cofator do elemento aij de uma matriz...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Menor Complementar
Menor complementar de um elemento de uma matriz é o determinante dela, eliminando a linha e a coluna que pertencer esse elemento. É possível calcular o menor complementar se a matriz for quadrada e de ordem maior ou igual a 2. Dada uma matriz de ordem...