Matemática
Veja mais:
Construção Geométrica da Parábola pelo Método de Werner
Construção Geométrica da Parábola com Régua e Compasso
Construção Geométrica da Parábola pelo Método de Ibn Sinan

- Parábola
. Parábola Definição Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d. PF = Pd Elementos principais...
- Geometria Analítica, Parábola
1 - Introdução Se você consultar o Novo Dicionário Brasileiro Melhoramentos - 7ª edição, obterá a seguinte definição para a parábola: "Curva plana, cujos pontos são eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz) ou curva...
- Construção Geométrica Da Parábola Pelo Método De Werner
No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque nessa...
- Construção Geométrica De Uma Parábola Pelo Método De Ibn Sinan
Uma breve história: Abu Said Sinan ibn Thabit ibn Qurra foi uma matemático, astrônomo que estudou geometria, além de ter sido extremamente eminente na medicina Nasceu por volta de 880 e também não se sabe exatamente a cidade onde nasceu, mas sabe-se...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
Matemática
Construção Geométrica da Parábola pelo Método das Mediatrizes
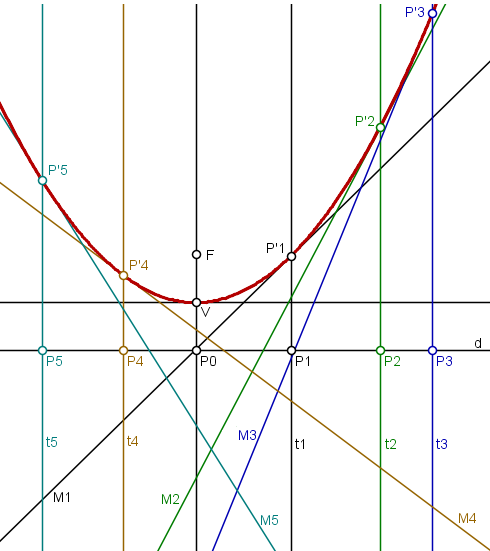
Este método, permite a construção de uma parábola a partir de seu foco $F$ e da reta diretriz $d$. Quando traçamos as mediatrizes do ponto $F$ e dos pontos $P_N$ sobre a diretriz, a envoltória criada pelas mediatrizes gera a parábola.

Dado um foco $F$ e uma reta diretriz $d$, podemos construir uma parábola como se segue:
$1)$ Trace o eixo de simetria da parábola, que passa pelo foco $F$ e é perpendicular à diretriz.
$2)$ Trace a mediatriz dos pontos $F$ e $P_0$, marcando o ponto $V$ na intersecção com o eixo de simetria. Este ponto é o vértice da parábola.
$3)$ Marque $P_1$ sobre qualquer ponto da diretriz, trace a mediatriz $M_1$ dos pontos $F$ e $P_1$ e trace a perpendicular $t_1$ por $P_1$. Marque o ponto $P'_1$ na intersecção da mediatriz $M_1$ com a perpendicular $t_1$.
$4)$ Marque quantos pontos $P_N$ desejar sobre a diretriz e proceda analogamente ao descrito no passo anterior para determinar os pontos $P'_N$.
$5)$ A reunião dos pontos $P'_N$ define uma parábola. Vejam que as mediatrizes $M_N$ são tangentes à parábola.
Este método pode ser obtido através da dobradura de um papel. Para ilustrar, sugiro que assistam este vídeo muito interessante:
Veja mais:
Construção Geométrica da Parábola pelo Método de Werner
Construção Geométrica da Parábola com Régua e Compasso
Construção Geométrica da Parábola pelo Método de Ibn Sinan

- Parábola
. Parábola Definição Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d. PF = Pd Elementos principais...
- Geometria Analítica, Parábola
1 - Introdução Se você consultar o Novo Dicionário Brasileiro Melhoramentos - 7ª edição, obterá a seguinte definição para a parábola: "Curva plana, cujos pontos são eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz) ou curva...
- Construção Geométrica Da Parábola Pelo Método De Werner
No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque nessa...
- Construção Geométrica De Uma Parábola Pelo Método De Ibn Sinan
Uma breve história: Abu Said Sinan ibn Thabit ibn Qurra foi uma matemático, astrônomo que estudou geometria, além de ter sido extremamente eminente na medicina Nasceu por volta de 880 e também não se sabe exatamente a cidade onde nasceu, mas sabe-se...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
