Matemática
. Parábola
Definição
Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d.
PF = Pd
Elementos principais
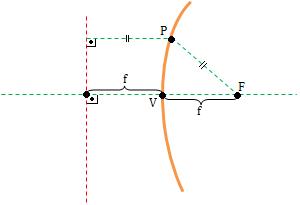
F é o foco
d é a diretriz
V é o vértice
p = 2 . f é o parâmetro (FV = Vd = f)
é o eixo das simetrias
Equação reduzida
Suponha a parábola da figura: eixo de simetria contido no eixo “x” e vértice na origem.
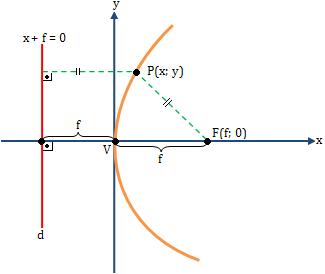
Referente ao sistema de eixos cartesianos, temos:
Foco: F(f; 0)
Diretriz: x = -f
Supondo P(x; y) como um ponto genérico da parábola, da definição PF = PD, resulta:
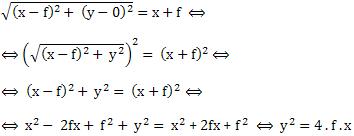
A equação: y2 = 4 . f . x
chamada de equação reduzida da parábola com eixo de simetria contido no eixo “x” e vértice na origem, quando a hipérbole estiver voltada para a direita.
Quando a parábola estiver voltada para a esquerda, sua equação reduzida será:
y2 = – 4 . f . x
Excentricidade
A excentricidade na parábola é a razão:
- Questão 49 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A equação x2 + (y ? 1)2 = 25 representa uma (A) circunferência. (B) elipse. (C) hipérbole. (D) parábola. (E) reta. Solução: (A) Aplicando o Método de Resolução de Problemas segundo Polya: 1° ? Compreensão do Problema Segundo a teoria...
- Cônicas
Geometria Analítica - CônicasElipse Considerando, num plano , dois pontos distintos, F1 e F2 , e sendo 2a um número real maior que a distância entre F1 e F2, chamamos de elipse o conjunto dos pontos do plano tais que a soma das distâncias...
- Como Encontrar O Foco E A Diretriz De Uma Parábola Com Régua E Compasso
Neste artigo veremos como encontrar o foco e a reta diretriz de uma parábola dada, utilizando para isso, apenas régua não-graduada e compasso. Para a construção da parábola, dispomos de $4$ métodos apresentados aqui no blog. Veja no rodapé deste...
- Construção Geométrica Da Parábola Pelo Método Das Mediatrizes
Este método, permite a construção de uma parábola a partir de seu foco $F$ e da reta diretriz $d$. Quando traçamos as mediatrizes do ponto $F$ e dos pontos $P_N$ sobre a diretriz, a envoltória criada pelas mediatrizes gera a parábola. Dado um foco...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
Matemática
Parábola
. Parábola
Definição
Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d.
PF = Pd
Elementos principais
F é o foco
d é a diretriz
V é o vértice
p = 2 . f é o parâmetro (FV = Vd = f)
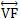é o eixo das simetriasEquação reduzida
Suponha a parábola da figura: eixo de simetria contido no eixo “x” e vértice na origem.
Referente ao sistema de eixos cartesianos, temos:
Foco: F(f; 0)
Diretriz: x = -f
Supondo P(x; y) como um ponto genérico da parábola, da definição PF = PD, resulta:
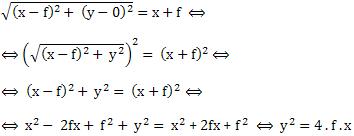
A equação: y2 = 4 . f . x
chamada de equação reduzida da parábola com eixo de simetria contido no eixo “x” e vértice na origem, quando a hipérbole estiver voltada para a direita.
Quando a parábola estiver voltada para a esquerda, sua equação reduzida será:
y2 = – 4 . f . x
Excentricidade
A excentricidade na parábola é a razão:
www.colegioweb.com.br
- Questão 49 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A equação x2 + (y ? 1)2 = 25 representa uma (A) circunferência. (B) elipse. (C) hipérbole. (D) parábola. (E) reta. Solução: (A) Aplicando o Método de Resolução de Problemas segundo Polya: 1° ? Compreensão do Problema Segundo a teoria...
- Cônicas
Geometria Analítica - CônicasElipse Considerando, num plano , dois pontos distintos, F1 e F2 , e sendo 2a um número real maior que a distância entre F1 e F2, chamamos de elipse o conjunto dos pontos do plano tais que a soma das distâncias...
- Como Encontrar O Foco E A Diretriz De Uma Parábola Com Régua E Compasso
Neste artigo veremos como encontrar o foco e a reta diretriz de uma parábola dada, utilizando para isso, apenas régua não-graduada e compasso. Para a construção da parábola, dispomos de $4$ métodos apresentados aqui no blog. Veja no rodapé deste...
- Construção Geométrica Da Parábola Pelo Método Das Mediatrizes
Este método, permite a construção de uma parábola a partir de seu foco $F$ e da reta diretriz $d$. Quando traçamos as mediatrizes do ponto $F$ e dos pontos $P_N$ sobre a diretriz, a envoltória criada pelas mediatrizes gera a parábola. Dado um foco...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...