Matemática
Neste artigo veremos como encontrar o foco e a reta diretriz de uma parábola dada, utilizando para isso, apenas régua não-graduada e compasso.
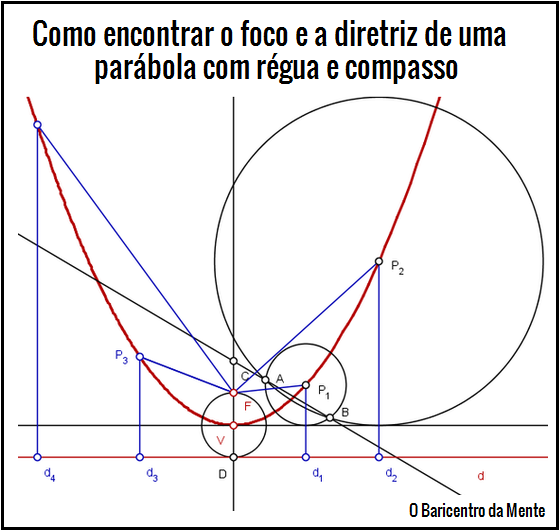
Para a construção da parábola, dispomos de $4$ métodos apresentados aqui no blog. Veja no rodapé deste artigo.
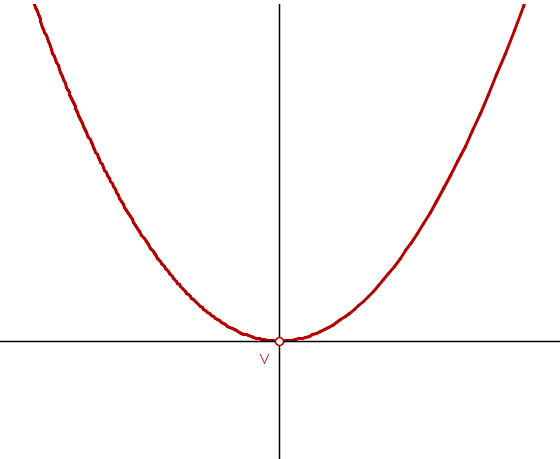
Dada uma parábola com sua concavidade voltada para cima e seu vértice $V$, traçamos seu eixo de simetria e a perpendicular passando por $V$. Se pensarmos no plano cartesiano, o eixo de simetria é o eixo dos $y$ e a perpendicular por $V$ é o eixo dos $x$ e o vértice da parábola está na origem.
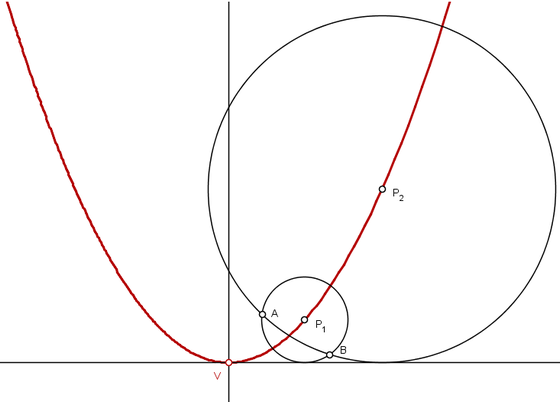
Descreva duas circunferências tangentes ao eixo horizontal de modo que seus centros sejam pontos de um mesmo ramo da parábola. Marque os pontos de intersecção dessas circunferências como $A$ e $B$.
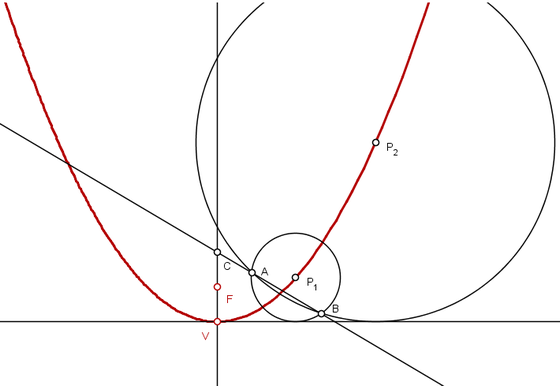
Trace um segmento passando pelos pontos $A$ e $B$ e marque a intersecção com o eixo de simetria como $C$. O ponto médio do segmento $\overline{VC}$ é o foco $F$ da parábola.
Para encontrarmos a reta diretriz, usamos a definição da parábola, que diz que a medida da parábola ao foco é igual à distância da parábola à reta diretriz. Centrada no vértice $V$, descrevemos uma circunferência de raio $\overline{VF}$. Pela intersecção com o eixo de simetria passa a reta diretriz, perpendicular a esta.
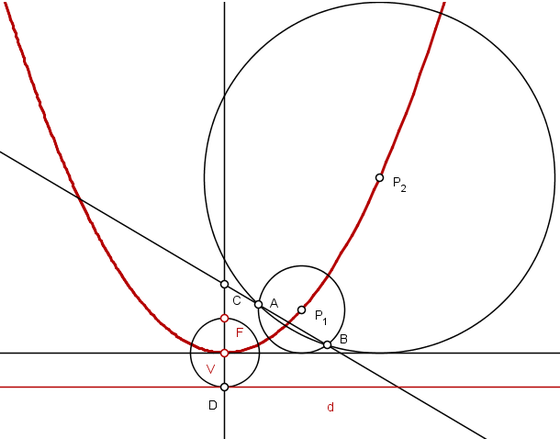
Escolhendo qualquer ponto da parábola, temos que a distância até o foco é a mesma até a reta diretriz.
Construção geométrica de uma parábola pelo método de Ibn Sinan
Construção geométrica de uma parábola pelo método de Werner
Construção geométrica de uma parábola pelo método das mediatrizes

- Gráfico Da Função Do 2º Grau
Gráfico da Função do 2º GrauMarcos Noé ParábolaO gráfico de uma função do 2º grau é dado por uma parábola com concavidade voltada para cima ou para baixo. A parábola intersecciona ou não, o eixo das abscissas (x),...
- Parábola
. Parábola Definição Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d. PF = Pd Elementos principais...
- Geometria Analítica, Parábola
1 - Introdução Se você consultar o Novo Dicionário Brasileiro Melhoramentos - 7ª edição, obterá a seguinte definição para a parábola: "Curva plana, cujos pontos são eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz) ou curva...
- Construção Geométrica Da Parábola Pelo Método De Werner
No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque nessa...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
Matemática
Como encontrar o foco e a diretriz de uma parábola com régua e compasso
Neste artigo veremos como encontrar o foco e a reta diretriz de uma parábola dada, utilizando para isso, apenas régua não-graduada e compasso.

Para a construção da parábola, dispomos de $4$ métodos apresentados aqui no blog. Veja no rodapé deste artigo.
Dada uma parábola com sua concavidade voltada para cima e seu vértice $V$, traçamos seu eixo de simetria e a perpendicular passando por $V$. Se pensarmos no plano cartesiano, o eixo de simetria é o eixo dos $y$ e a perpendicular por $V$ é o eixo dos $x$ e o vértice da parábola está na origem.

Descreva duas circunferências tangentes ao eixo horizontal de modo que seus centros sejam pontos de um mesmo ramo da parábola. Marque os pontos de intersecção dessas circunferências como $A$ e $B$.

Trace um segmento passando pelos pontos $A$ e $B$ e marque a intersecção com o eixo de simetria como $C$. O ponto médio do segmento $\overline{VC}$ é o foco $F$ da parábola.

Para encontrarmos a reta diretriz, usamos a definição da parábola, que diz que a medida da parábola ao foco é igual à distância da parábola à reta diretriz. Centrada no vértice $V$, descrevemos uma circunferência de raio $\overline{VF}$. Pela intersecção com o eixo de simetria passa a reta diretriz, perpendicular a esta.

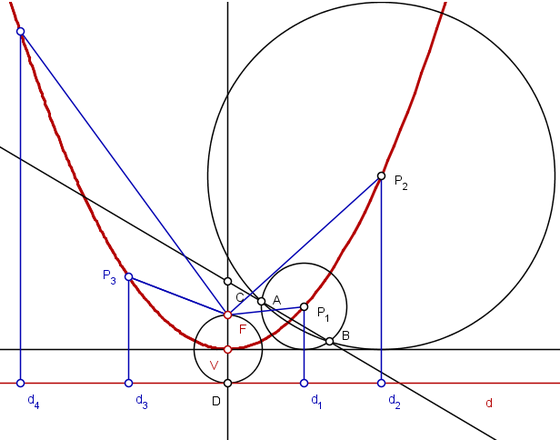
Escolhendo qualquer ponto da parábola, temos que a distância até o foco é a mesma até a reta diretriz.

Construção elaborada por: Bruno Henrique de Abreu
Compilador cristão
Compilador cristão
Veja mais:
Construção geométrica de uma parábola com régua e compassoConstrução geométrica de uma parábola pelo método de Ibn Sinan
Construção geométrica de uma parábola pelo método de Werner
Construção geométrica de uma parábola pelo método das mediatrizes

- Gráfico Da Função Do 2º Grau
Gráfico da Função do 2º GrauMarcos Noé ParábolaO gráfico de uma função do 2º grau é dado por uma parábola com concavidade voltada para cima ou para baixo. A parábola intersecciona ou não, o eixo das abscissas (x),...
- Parábola
. Parábola Definição Considerando um ponto F (foco) e uma reta d (diretriz), sendo F ∉ d, pertencentes a um mesmo plano, definimos parábola como o lugar geométrico dos pontos P do plano eqüidistante do ponto F e da reta d. PF = Pd Elementos principais...
- Geometria Analítica, Parábola
1 - Introdução Se você consultar o Novo Dicionário Brasileiro Melhoramentos - 7ª edição, obterá a seguinte definição para a parábola: "Curva plana, cujos pontos são eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz) ou curva...
- Construção Geométrica Da Parábola Pelo Método De Werner
No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque nessa...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
