Matemática

Werner produziu uma obra importante para a Geometria sobre Elementos de Cônicas, em latim, dividida em $22$ volumes, impressa em Nüremberg em $1522$.
Veja mais:
Construção Geométrica da Parábola com Régua e Compasso
Construção Geométrica da Parábola pelo Método de Ibn Sinan
Construção Geométrica da Hipérbole com Régua e Compasso

- Como Achar O Centro Do Círculo, Por Euclides
No livro $III$ dos Elementos, Proposição $1$, Euclides nos mostra como achar o centro de um círculo dado de maneira muito elementar e elegante. Proposição $1$ do Livro $III$: Achar o centro do círculo dado. Seja o círculo $C_1$. Tracemos através...
- Construção Geométrica Da Parábola Pelo Método Das Mediatrizes
Este método, permite a construção de uma parábola a partir de seu foco $F$ e da reta diretriz $d$. Quando traçamos as mediatrizes do ponto $F$ e dos pontos $P_N$ sobre a diretriz, a envoltória criada pelas mediatrizes gera a parábola. Dado um foco...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
Matemática
Construção Geométrica da Parábola pelo Método de Werner
No século $XVI$, as contribuições em Geometria foram menos espetaculares do que em Álgebra ou em Trigonometria, mas alguns nomes como Francesco Maurolico e Pacioli, na Itália, e Albrecht Dürer e Johannes Werner, na Alemanha, tiveram destaque nessa época.

Werner produziu uma obra importante para a Geometria sobre Elementos de Cônicas, em latim, dividida em $22$ volumes, impressa em Nüremberg em $1522$.
Werner estava preocupado com o problema da duplicação do cubo e, então, concentrou-se muito com curvas como a parábola e a hipérbole. Ele dá uma construção interessante, utilizando apenas régua e compasso:
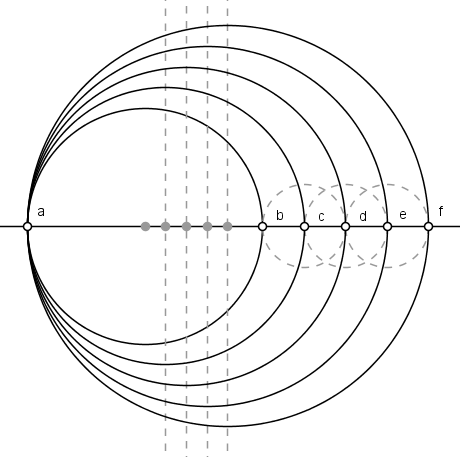
$1)$ Num eixo horizontal, descrevemos um feixe de circunferências tangentes entre si no ponto $a$, cortando o eixo normal nos pontos $b$, $c$, $d$, $e$, $f$, $\cdots$, de modo que as distâncias $\overline{bc}=\overline{cd}=\overline{de}=\cdots$.

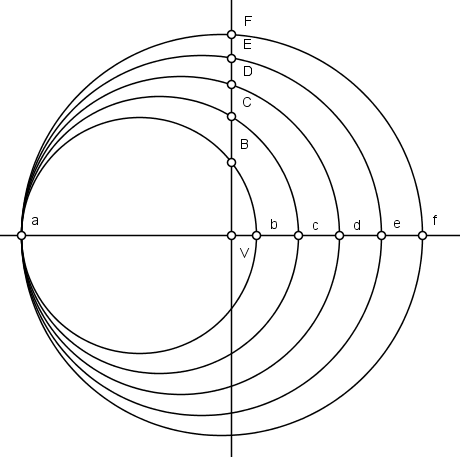
$2)$ Marcamos uma distância $\overline{aV}$ igual a um parâmetro desejado sobre a normal e por $V$ traçamos uma perpendicular, cortando as circunferências nos pontos $B$, $C$, $D$, $E$, $F$, $\cdots$, respectivamente.

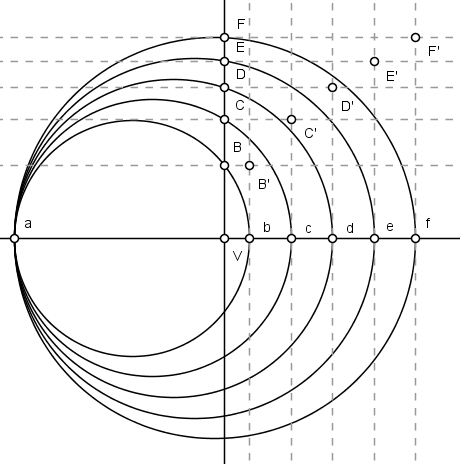
$3)$ Por $b$, traçamos os segmentos $\overline{bB'}$ e $\overline{bB''}$, perpendiculares à normal e de comprimento igual à $\overline{VB}$. Obtemos facilmente traçando paralelas à normal no ponto $B$. Por $c$, traçamos os segmentos $\overline{cC'}$ e $\overline{cC''}$, perpendiculares à normal e de comprimento igual à $\overline{VC}$. Procedemos analogamente para os pontos $d$, $e$, $f$, $\cdots$

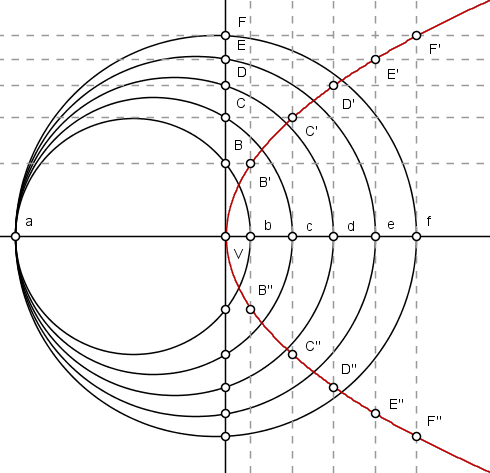
$4)$ Os pontos $B'$, $B''$, $C'$, $C''$, $D'$, $D''$, $\cdots$ estão sobre a parábola de vértice $V$, cujo eixo de simetria é a normal.

Referências:
[1] História da Matemática - Carl Boyer
[1] História da Matemática - Carl Boyer
Veja mais:
Construção Geométrica da Parábola com Régua e Compasso
Construção Geométrica da Parábola pelo Método de Ibn Sinan
Construção Geométrica da Hipérbole com Régua e Compasso

- Como Achar O Centro Do Círculo, Por Euclides
No livro $III$ dos Elementos, Proposição $1$, Euclides nos mostra como achar o centro de um círculo dado de maneira muito elementar e elegante. Proposição $1$ do Livro $III$: Achar o centro do círculo dado. Seja o círculo $C_1$. Tracemos através...
- Construção Geométrica Da Parábola Pelo Método Das Mediatrizes
Este método, permite a construção de uma parábola a partir de seu foco $F$ e da reta diretriz $d$. Quando traçamos as mediatrizes do ponto $F$ e dos pontos $P_N$ sobre a diretriz, a envoltória criada pelas mediatrizes gera a parábola. Dado um foco...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...
- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...
