Matemática
1 - O uso do Determinante de terceira ordem na Geometria Analítica
1.1 - Área de um triângulo
Seja o triângulo ABC de vértices A(xa , ya) , B(xb , xc) e C(xc , yc) . A área S desse triângulo é dada por
S = 1/2 . | D | onde ½ D½ é o módulo do determinante formado pelas coordenadas dos vértices A , B e C .
Temos portanto:
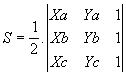
A área S é normalmente expressa em u.a. (unidades de área)
Para o cálculo do determinante de terceira ordem, utilizamos a conhecida e prática regra de Sarrus.
1.2 - Condição de alinhamento de três pontos
Três pontos estão alinhados se são colineares , isto é , se pertencem a uma mesma reta .
É óbvio que se os pontos A , B e C estão alinhados , então o triângulo ABC não existe , e podemos pois considerar que sua área é nula ( S = 0 ) .
Fazendo S = 0 na fórmula de área do item 1.1 , concluímos que a condição de alinhamento dos 3 pontos é que o determinante D seja nulo , ou seja : D = 0 .
a) 4
b) 3
c) 3,5
d) 4,5
e) 2
Solução:
Para que estes pontos estejam alinhados (pontos colineares), deveremos ter:
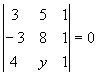
Desenvolvendo o determinante pela Regra de Sarrus, obtemos:
- 32 - 3y + 15 + 24 - 3y + 20 = 0 \ y = 9/2 = 4,5.
Portanto a alternativa correta é a letra D.
2 - Equação geral da reta.
Seja r a reta que passa pelos pontos A(xa , ya) e B(xb , yb).
Seja P(x , y) um ponto qualquer desta reta . Pela condição de alinhamento de 3 pontos , podemos escrever:
Desenvolvendo o determinante acima obtemos:
(Ya - Yb) . x + (Xa - Xb) . y + (XaYb - XbYa) = 0 .
Fazendo Ya - Yb = a , Xa - Xb = b e XaYb - XbYa = c , decorre que todo ponto P(x,y) pertencente à reta , deve verificar a equação :
ax + by + c = 0
que é chamada equação geral da reta r .
Exemplos:
2x + 5y - 4 = 0 (a = 2 , b = 5 , c = -4)
3x - 4y = 10 (a = 3 , b = -4 , c = -10); observe que podemos escrever 3x - 4y - 10 = 0.
3y + 12 = 0 (a = 0 , b = 3 , c = 12)
7x + 14 = 0 (a = 7 , b = 0 , c = 14)
x = 0 (a = 1 , b = 0 , c = 0) ordenadas .® equação do eixo Oy - eixo das
y = 0 (a = 0 , b = 1 , c = 0) ® equação do eixo Ox - eixo das abscissas .
Observações:a) a = 0 ® y = - c/b (reta paralela ao eixo dos x )
b) b = 0 ® x = - c/a (reta paralela ao eixo dos y)
3 - Posição relativa de duas retas
Sabemos da Geometria que duas retas r e s no plano podem ser :
Paralelas : r Ç s = Æ
Concorrentes : r Ç s = { P } , onde P é o ponto de interseção .
Coincidentes : r = s.
Dadas as retas r : ax + by + c = 0 e s : a’x + b’y + c’ = 0 , temos os seguintes casos :
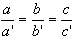® as retas são coincidentes .
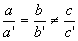® as retas são paralelas .
a) elas são paralelas
b) elas são concorrentes
c) r Ç t Ç s = R
d) r Ç s Ç t = R2
e) as três equações representam uma mesma reta .
Solução:
Primeiro vamos verificar as retas r e s: 3 / 9 = 2 / 6 = -15 / -45 (primeiro caso acima) e portanto as
retas r e s são coincidentes.
Comparando agora, por exemplo a reta r com a reta t , teremos:
3 / 12 = 2 / 8 = -15 / -60 (primeiro caso acima);
Portanto as retas r, s e t são coincidentes, ou seja, representam a mesma reta.
Logo a alternativa correta é a letra E.
3) Para se determinar o ponto de interseção de duas retas , basta resolver o sistema de equações formado pelas equações das retas. Nestas condições , pede-se calcular as coordenadas do ponto de interseção das retas r : 2x + 5y - 18 = 0 e s : 6x - 7y - 10 = 0.
Solução:Da equação da reta r tiramos: x = (18 - 5y) / 2 (eq. 1);
substituindo na equação da reta s vem:
6[(18-5y) / 2] - 7y -10 = 0 \ 54 - 15y - 7y - 10 = 0 \ 44 - 22y = 0 \ 44 = 22y \ y = 2;
substituindo o valor de y na eq. 1 fica: .x = (18 - 5.2) / 2 = 4.
Portanto o ponto de interseção é o ponto P(4,2).
Agora resolva esta:
Qual a área do triângulo ABC de vértices A(2,5), B(0,3) e C(1,1)?
Resposta: S = 3 u.a. (3 unidades de área)
www.algosobre.com.br
- Retas Paralelas
No estudo analítico da reta não podemos deixar de falar das posições relativas entre retas. Dadas duas ou mais retas do plano, elas podem ser paralelas, concorrentes, coincidentes ou concorrentes perpendiculares. Abordaremos aqui o paralelismo de...
- Condição De Concorrência De Duas Retas
Dado um ponto P qualquer de coordenadas (x0,y0) comum a duas retas r e s, dizemos que as retas são concorrentes em P. Dessa forma, as coordenadas do ponto P satisfazem a equação das retas r e s. Dada as retas r: a1x + b1y + c1 = 0 e s:a2x + b2y + c2...
- Retas
Quando representamos uma reta no plano cartesiano ela poderá, em alguns casos, formar com o eixo Ox ou com o Oy um ângulo de 90°. Essas retas recebem um nome especifico: Retas verticais e retas horizontais. • Retas verticais São retas que interceptam...
- Equação Da Reta
Em um plano cartesiano as retas podem ser paralelas ou coincidentes, se no ponto comum as duas retas formarem um ângulo de 90° graus podemos dizer que são perpendiculares, para que isso seja verdade os seus coeficientes deverão ser o oposto do inverso...
- Equação Geral Da Reta
Equação geral da retaMarcelo Rigonatto Equação geralVamos considerar uma reta s que passe pelos pontos A(x1, y1) e B(x2, y2), sendo P(x, y) um ponto qualquer dessa mesma reta s. Como os pontos A, B e P pertencem a uma mesma...
Matemática
Geometria Analítica
1 - O uso do Determinante de terceira ordem na Geometria Analítica
1.1 - Área de um triângulo
Seja o triângulo ABC de vértices A(xa , ya) , B(xb , xc) e C(xc , yc) . A área S desse triângulo é dada por
S = 1/2 . | D | onde ½ D½ é o módulo do determinante formado pelas coordenadas dos vértices A , B e C .
Temos portanto:
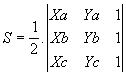
A área S é normalmente expressa em u.a. (unidades de área)
Para o cálculo do determinante de terceira ordem, utilizamos a conhecida e prática regra de Sarrus.
1.2 - Condição de alinhamento de três pontos
Três pontos estão alinhados se são colineares , isto é , se pertencem a uma mesma reta .
É óbvio que se os pontos A , B e C estão alinhados , então o triângulo ABC não existe , e podemos pois considerar que sua área é nula ( S = 0 ) .
Fazendo S = 0 na fórmula de área do item 1.1 , concluímos que a condição de alinhamento dos 3 pontos é que o determinante D seja nulo , ou seja : D = 0 .
Exercício resolvido:
Se os pontos P(3 , 5) , Q(-3 , 8) e C(4 , y) são colineares , então o valor de y é : a) 4
b) 3
c) 3,5
d) 4,5
e) 2
Solução:
Para que estes pontos estejam alinhados (pontos colineares), deveremos ter:
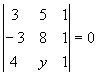
Desenvolvendo o determinante pela Regra de Sarrus, obtemos:
- 32 - 3y + 15 + 24 - 3y + 20 = 0 \ y = 9/2 = 4,5.
Portanto a alternativa correta é a letra D.
2 - Equação geral da reta.
Seja r a reta que passa pelos pontos A(xa , ya) e B(xb , yb).
Seja P(x , y) um ponto qualquer desta reta . Pela condição de alinhamento de 3 pontos , podemos escrever:
Desenvolvendo o determinante acima obtemos:
(Ya - Yb) . x + (Xa - Xb) . y + (XaYb - XbYa) = 0 .
Fazendo Ya - Yb = a , Xa - Xb = b e XaYb - XbYa = c , decorre que todo ponto P(x,y) pertencente à reta , deve verificar a equação :
ax + by + c = 0
que é chamada equação geral da reta r .
Exemplos:
2x + 5y - 4 = 0 (a = 2 , b = 5 , c = -4)
3x - 4y = 10 (a = 3 , b = -4 , c = -10); observe que podemos escrever 3x - 4y - 10 = 0.
3y + 12 = 0 (a = 0 , b = 3 , c = 12)
7x + 14 = 0 (a = 7 , b = 0 , c = 14)
x = 0 (a = 1 , b = 0 , c = 0) ordenadas .® equação do eixo Oy - eixo das
y = 0 (a = 0 , b = 1 , c = 0) ® equação do eixo Ox - eixo das abscissas .
Observações:a) a = 0 ® y = - c/b (reta paralela ao eixo dos x )
b) b = 0 ® x = - c/a (reta paralela ao eixo dos y)
3 - Posição relativa de duas retas
Sabemos da Geometria que duas retas r e s no plano podem ser :
Paralelas : r Ç s = Æ
Concorrentes : r Ç s = { P } , onde P é o ponto de interseção .
Coincidentes : r = s.
Dadas as retas r : ax + by + c = 0 e s : a’x + b’y + c’ = 0 , temos os seguintes casos :
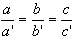® as retas são coincidentes . 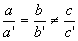® as retas são paralelas .  | as retas são concorrentes . |
Exercícios resolvidos
1 - OSEC-SP - Qual a posição relativa das retas r : x + 2y + 3 = 0 e s: 4x + 8y + 10 = 0 ?
Solução:
Temos que: 1 / 4 = 2 / 8 ¹ 3 / 10 (segundo caso acima) e, portanto as retas são paralelas.
2 - Dadas as retas r : 3x + 2y - 15 = 0 ; s : 9x + 6y - 45 = 0 e t : 12x + 8y - 60 = 0 , podemos afirmar:1 - OSEC-SP - Qual a posição relativa das retas r : x + 2y + 3 = 0 e s: 4x + 8y + 10 = 0 ?
Solução:
Temos que: 1 / 4 = 2 / 8 ¹ 3 / 10 (segundo caso acima) e, portanto as retas são paralelas.
a) elas são paralelas
b) elas são concorrentes
c) r Ç t Ç s = R
d) r Ç s Ç t = R2
e) as três equações representam uma mesma reta .
Solução:
Primeiro vamos verificar as retas r e s: 3 / 9 = 2 / 6 = -15 / -45 (primeiro caso acima) e portanto as
retas r e s são coincidentes.
Comparando agora, por exemplo a reta r com a reta t , teremos:
3 / 12 = 2 / 8 = -15 / -60 (primeiro caso acima);
Portanto as retas r, s e t são coincidentes, ou seja, representam a mesma reta.
Logo a alternativa correta é a letra E.
3) Para se determinar o ponto de interseção de duas retas , basta resolver o sistema de equações formado pelas equações das retas. Nestas condições , pede-se calcular as coordenadas do ponto de interseção das retas r : 2x + 5y - 18 = 0 e s : 6x - 7y - 10 = 0.
Solução:Da equação da reta r tiramos: x = (18 - 5y) / 2 (eq. 1);
substituindo na equação da reta s vem:
6[(18-5y) / 2] - 7y -10 = 0 \ 54 - 15y - 7y - 10 = 0 \ 44 - 22y = 0 \ 44 = 22y \ y = 2;
substituindo o valor de y na eq. 1 fica: .x = (18 - 5.2) / 2 = 4.
Portanto o ponto de interseção é o ponto P(4,2).
Agora resolva esta:
Qual a área do triângulo ABC de vértices A(2,5), B(0,3) e C(1,1)?
Resposta: S = 3 u.a. (3 unidades de área)
www.algosobre.com.br
- Retas Paralelas
No estudo analítico da reta não podemos deixar de falar das posições relativas entre retas. Dadas duas ou mais retas do plano, elas podem ser paralelas, concorrentes, coincidentes ou concorrentes perpendiculares. Abordaremos aqui o paralelismo de...
- Condição De Concorrência De Duas Retas
Dado um ponto P qualquer de coordenadas (x0,y0) comum a duas retas r e s, dizemos que as retas são concorrentes em P. Dessa forma, as coordenadas do ponto P satisfazem a equação das retas r e s. Dada as retas r: a1x + b1y + c1 = 0 e s:a2x + b2y + c2...
- Retas
Quando representamos uma reta no plano cartesiano ela poderá, em alguns casos, formar com o eixo Ox ou com o Oy um ângulo de 90°. Essas retas recebem um nome especifico: Retas verticais e retas horizontais. • Retas verticais São retas que interceptam...
- Equação Da Reta
Em um plano cartesiano as retas podem ser paralelas ou coincidentes, se no ponto comum as duas retas formarem um ângulo de 90° graus podemos dizer que são perpendiculares, para que isso seja verdade os seus coeficientes deverão ser o oposto do inverso...
- Equação Geral Da Reta
Equação geral da retaMarcelo Rigonatto Equação geralVamos considerar uma reta s que passe pelos pontos A(x1, y1) e B(x2, y2), sendo P(x, y) um ponto qualquer dessa mesma reta s. Como os pontos A, B e P pertencem a uma mesma...