Matemática
(x-a)^2+(y-b)^2=r^2
\end{equation}
x^2+y^2=r^2
\end{equation}
x^2+(y-2)^2=4\\
(x-1)^2+y^2=1
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2+y^2-4y=0\\
x^2-2x+y^2=0
\end{matrix}\right.$$
y_1=0 \Rightarrow x_1=0\\
y_2=\frac{4}{5} \Rightarrow x_2=\frac{8}{5}
\end{matrix}
P_1=(0,0) \qquad \text{e} \qquad P_2=\left(\frac{8}{5},\frac{4}{5} \right)
\end{equation*}
C_1 \cap C_2=\left \{ (0,0),\left(\frac{8}{5},\frac{4}{5}\right)\right \}
\end{equation*}
x^2+y^2=4\\
(x-4)^2+y^2=36
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2+y^2=4\\
x^2-8x+y^2=20
\end{matrix}\right.$$
x=-2 \Rightarrow y=0
\end{equation*}
P_1=(-2,0)
\end{equation*}
O conjunto solução é:
\begin{equation*}
C_1 \cap C_2={(-2,0)}
\end{equation*}
Graficamente, temos:
(x-2)^2+(y-2)^2=1\\
x^2+(y-2)^2=49
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2-4x+y^2-4y=-7\\
x^2+y^2-4y=45
\end{matrix}\right.$$
Resolvendo o sistema, encontramos:
\begin{equation*}
x=13
\end{equation*}
y=\frac{4\pm \sqrt{-480}}{2}
\end{equation*}
O conjunto solução é:
\begin{equation*}
C_1 \cap C_2 ={\phi}
\end{equation*}
Graficamente, temos:
Veja mais:
Como Encontrar o centro de uma Circunferência
Retificando uma Circunferência
Ângulo entre Circunferências e Circunferências Ortogonais

- Razão De Secção
Consideremos três pontos: $A(x_a,y_a)$, $B(x_b,y_b)$ e $C(x_c,y_c)$, pertencentes a uma mesma reta $r$, oblíqua aos eixos $x$ e $y$ e ainda sendo $B$ e $C$ distintos. Definição:A razão $k$ das medidas algébricas de $\overline{AC}$ e $\overline{CB}$...
- Resolução Da Integral $\int \frac{1}{(x^2-1)^2}dx$
Integrais por frações parciais às vezes podem ser complicadas de serem resolvidas. Às vezes é mais complicado encontrar as frações parciais equivalente ao integrando do que resolver as integrais obtidas após este processo. Este é um exemplo interessante...
- Os $10$ Problemas De Apolônio: Problema $1:[ppp]$ Problema Dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares. Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
Matemática
Intersecção de Circunferências
A equação da circunferência é dada por:
\begin{equation}(x-a)^2+(y-b)^2=r^2
\end{equation}
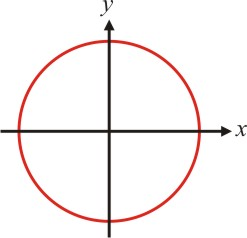
Onde $a$ e $b$ são as coordenadas do centro da circunferência e $r$ é o raio da circunferência. Se a circunferência for centrada na origem, a equação $(1)$ se transforma em:
\begin{equation}x^2+y^2=r^2
\end{equation}
Graficamente, temos:

Sejam duas circunferências $C_1$ e $C_2$. A intersecção dessas duas circunferências é determinada pelos pontos $P(x,y)$ que pertencem a ambas as curvas, satisfazendo o sistema formado por suas equações. Podemos encontrar $3$ situações possíveis:
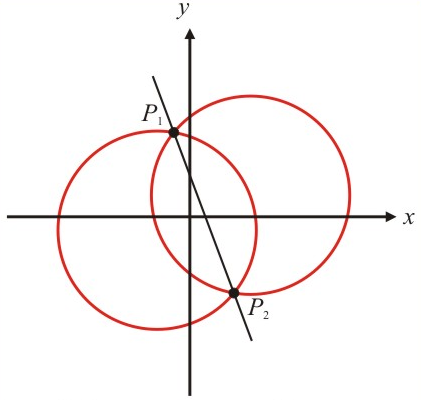
$1)$ Dois pontos em comum $P_1$ e $P_2$. Isso implica que o sistema de equações admite duas soluções: $P_1(x_1,y_1)$ e $P_2(x_2,y_2)$. Graficamente:

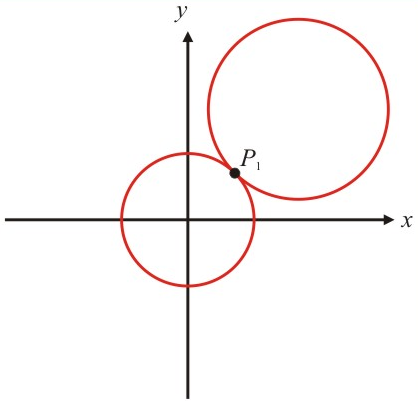
$2)$ Um ponto em comum $P(x,y)$. Isso implica que o sistema de equações admite apenas uma solução real: $P(x,y)$. Graficamente:

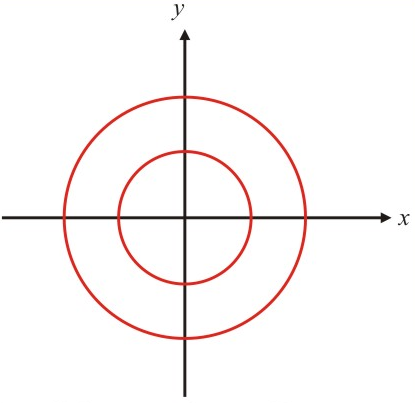
$3)$ Nenhum ponto em comum, ou seja, $C_1 \cap C_2 = \phi $. Isso implica que o sistema de equações é impossível. Graficamente:

Vamos resolver alguns exemplos para melhor esclarecimento.
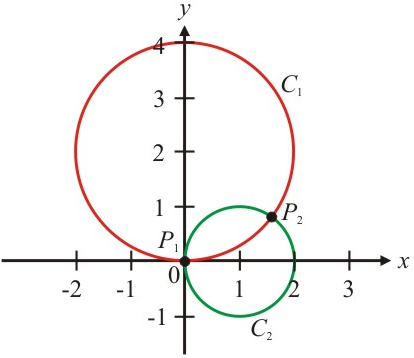
Exemplo $1$: Seja obter a intersecção entre as circunferências $C_1$ e $C_2$, cujas equações são: $C_1: \: x^2+(y-2)^2=4$ e $C_2: \: (x-1)^2+y^2=1$.
Podemos montar o seguinte sistema com as equações:
$$\left\{\begin{matrix}x^2+(y-2)^2=4\\
(x-1)^2+y^2=1
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2+y^2-4y=0\\
x^2-2x+y^2=0
\end{matrix}\right.$$
Resolvendo o sistema, encontramos os valores:
\begin{matrix}y_1=0 \Rightarrow x_1=0\\
y_2=\frac{4}{5} \Rightarrow x_2=\frac{8}{5}
\end{matrix}
Desta forma, as circunferências interceptam-se nos pontos:
\begin{equation*}P_1=(0,0) \qquad \text{e} \qquad P_2=\left(\frac{8}{5},\frac{4}{5} \right)
\end{equation*}
O conjunto solução é:
\begin{equation*}C_1 \cap C_2=\left \{ (0,0),\left(\frac{8}{5},\frac{4}{5}\right)\right \}
\end{equation*}
Graficamente, temos:

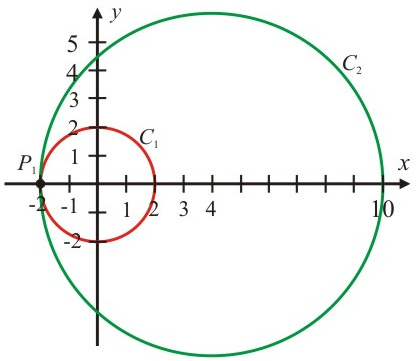
Exemplo $2$: Seja obter a intersecção entre as circunferências $C_1$ e $C_2$, cujas equações são: $C_1: \: x^2+y^2=4$ e $C_2: \: (x-4)^2+y^2=36$.
Podemos montar o seguinte sistema de equações:
$$\left\{\begin{matrix}x^2+y^2=4\\
(x-4)^2+y^2=36
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2+y^2=4\\
x^2-8x+y^2=20
\end{matrix}\right.$$
Resolvendo o sistema, encontramos apenas um valor para $x$:
\begin{equation*}x=-2 \Rightarrow y=0
\end{equation*}
Logo, as circunferências interceptam-se em apenas um ponto:
\begin{equation*}P_1=(-2,0)
\end{equation*}
O conjunto solução é:
\begin{equation*}
C_1 \cap C_2={(-2,0)}
\end{equation*}
Graficamente, temos:

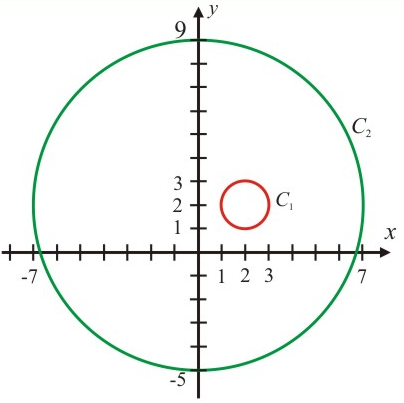
Exemplo $3$: Seja obter a intersecção entre as circunferências $C_1$ e $C_2$, cujas equações são: $C_1: \: (x-2)^2+(y-2)^2=1$ e $C_2: \: x^2+(y-2)^2=49$.
Podemos montar o seguinte sistema de equações:
$$\left\{\begin{matrix}(x-2)^2+(y-2)^2=1\\
x^2+(y-2)^2=49
\end{matrix}\right.
\Rightarrow
\left\{\begin{matrix}
x^2-4x+y^2-4y=-7\\
x^2+y^2-4y=45
\end{matrix}\right.$$
Resolvendo o sistema, encontramos:
\begin{equation*}
x=13
\end{equation*}
Se substituirmos este valor de $x$ na primeira equação, chegamos a uma equação do segundo grau, cujo discriminante $\Delta$ é negativo:
\begin{equation*}y=\frac{4\pm \sqrt{-480}}{2}
\end{equation*}
Isso implica dizer que o sistema é impossível. Logo, não há intersecção entre as circunferências.
O conjunto solução é:
\begin{equation*}
C_1 \cap C_2 ={\phi}
\end{equation*}
Graficamente, temos:

Veja mais:
Como Encontrar o centro de uma Circunferência
Retificando uma Circunferência
Ângulo entre Circunferências e Circunferências Ortogonais

- Razão De Secção
Consideremos três pontos: $A(x_a,y_a)$, $B(x_b,y_b)$ e $C(x_c,y_c)$, pertencentes a uma mesma reta $r$, oblíqua aos eixos $x$ e $y$ e ainda sendo $B$ e $C$ distintos. Definição:A razão $k$ das medidas algébricas de $\overline{AC}$ e $\overline{CB}$...
- Resolução Da Integral $\int \frac{1}{(x^2-1)^2}dx$
Integrais por frações parciais às vezes podem ser complicadas de serem resolvidas. Às vezes é mais complicado encontrar as frações parciais equivalente ao integrando do que resolver as integrais obtidas após este processo. Este é um exemplo interessante...
- Os $10$ Problemas De Apolônio: Problema $1:[ppp]$ Problema Dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares. Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
