Matemática
“Eu vi um professor de Matemática, só porque foi grande em sua vocação, ser enterrado como um rei que tivesse feito o bem para seus súditos.”
Foi assim que Voltaire se pronunciou após haver assistido aos funerais de Newton. De fato, o respeito pela obra científica de Newton conseguira transcender em muito o âmbito da comunidade especializada. Tanto que um sentimento de admiração generalizada cercou as últimas décadas de sua vida. Um episódio, porém, tinha turvado em parte a glória que pôde colher ainda em vida: a polêmica com Leibniz sobre a primazia da criação do cálculo.

Gottfried Wilhelm Leibniz $(1646-1716)$ nasceu em Leipzig, filho de um jurista, professor da universidade local. Órfão de pais aos $6$ anos de idade, foi em grande parte o responsável pela própria educação. Assim é que, revelando extrema precocidade intelectual, ainda em criança conseguiu aprender latim e grego sozinho. Já graduado em Direito em Leipzig, em $1667$ obtém o grau de doutor em Filosofia na Universidade de Altdorf com a tese Ars combinatória (A arte da combinação), uma tentativa de criar um método universal de raciocínio, através de uma espécie de cálculo, numa antecipação da Álgebra de Boole do século $XIX$. Mas sua formação matemática ainda era precária, como ele próprio reconheceria futuramente.
Esta tese valeu um convite para ser professor de Direito na própria Universidade de Altdorf. Mas sua aspiração era a carreira pública diplomática, que efetivamente veio a exercer por toda a vida, os últimos $40$ anos junto à corte de Hanover.
A primeira missão diplomática de Leibniz no exterior, que acabou se estendendo de $1672$ a $1676$, em Paris, se politicamente não deixou marcas, no campo da matemática foi da mais alta importância. Dois fatores, principalmente, pesaram muito nesse sentido: a amizade que Leibniz travou com Huygens, que na época morava em Paris e se tornou seu orientador em matemática; e uma viagem que fez a Londres em $1673$, na qual tomou conhecimento da obra de Barrow e, talvez, da primeira versão do cálculo de Newton (aí o embrião da futura controvérsia). Numa segunda ida a Londres em $1676$, Leibniz já desenvolvera os principais aspectos e notações do seu cálculo.
Se para Newton a ideia central do cálculo era a de taxa de variação (velocidade), para Leibniz era a de diferencial. Embora sem dar uma definição precisa (nem havia como), diferencial para Leibniz era uma diferença entre dois valores infinitamente próximos de uma variável. Muito mais preocupado do que Newton com simbologia, fórmulas e regras, Leibniz acabou optando pela notação $dx$, $dy$, $\cdots$ para as diferenciais de $x$, $y$, $\cdots$, respectivamente. E num artigo de $1682$ estabeleceu regras como:
\begin{gather}
da=a, \quad \text{se}\ a\ \text{é constante}\\
d(u+v)=du+dv\\
d(uv) = udv+vdu
\end{gather}
Na dedução de $(3)$ desprezou $(du)(dv)$ (sempre procedia assim com produtos de diferenciais)
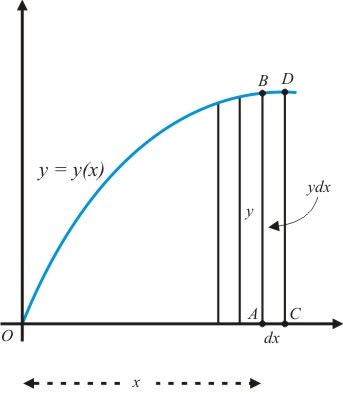
Seu cálculo integral foi explicado noutro artigo, dois anos depois. A relação deste com o cálculo diferencial, cerne da questão, é focalizada em termos de somatórios de áreas infinitesimais. Cada uma destas sob a curva $y = y(x)$ é dada por é dada por $y\ dx$. Para a soma de todas inventou o símbolo $\displaystyle \int$ (um $S$ alongado). Logo a área total sob a curva $y = y(x)$ é:
\begin{equation}
\int y\ dx
\end{equation}
Sendo a $\text{Área} (OCD) - \text{Área} (OAB) = y\ dx$ a diferencial da área, então:
\begin{equation}
d\int y\ dx = y\ dx
\end{equation}
O que mostra a invertibilidade de $d$ e $\displaystyle \int$.
Hoje não há dúvidas de que Newton e Leibniz seguiram linhas diferentes na criação do cálculo. Mas o segundo levou a pior na polêmica entre ambos, o que contribuiu para que tivesse um fim obscuro. O que diria Voltaire se assistisse ao enterro de Leibniz, no qual o único acompanhante era o fiel secretário do falecido?
Método de Integração por Partes
O Cálculo de Leibniz Parte 1, Parte 2 e Parte 3 no Blog Fatos Matemáticos

- Leibniz
O matemático e filósofo alemão Gottfried Wilhelm von Leibniz, nasceu em 1º de julho de 1646, e morreu em 14 de novembro de 1716. Foi um gênio universal e um fundador de ciência moderna. Ele antecipou o desenvolvimento de lógica simbólica...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
- O Cálculo Integral: O Cálculo Da Áreas
A busca de processos exatos ou mesmo aproximados para o cálculo de área $S$ da região limitada por uma curva fechada deu a Arquimedes (século $IIIa.C.$ aproximadamente) a glória de ser considerado um dos maiores matemáticos de todos os tempos. Com...
Matemática
Leibniz e as Diferenciais
“Eu vi um professor de Matemática, só porque foi grande em sua vocação, ser enterrado como um rei que tivesse feito o bem para seus súditos.”
Foi assim que Voltaire se pronunciou após haver assistido aos funerais de Newton. De fato, o respeito pela obra científica de Newton conseguira transcender em muito o âmbito da comunidade especializada. Tanto que um sentimento de admiração generalizada cercou as últimas décadas de sua vida. Um episódio, porém, tinha turvado em parte a glória que pôde colher ainda em vida: a polêmica com Leibniz sobre a primazia da criação do cálculo.

Gottfried Wilhelm Leibniz $(1646-1716)$ nasceu em Leipzig, filho de um jurista, professor da universidade local. Órfão de pais aos $6$ anos de idade, foi em grande parte o responsável pela própria educação. Assim é que, revelando extrema precocidade intelectual, ainda em criança conseguiu aprender latim e grego sozinho. Já graduado em Direito em Leipzig, em $1667$ obtém o grau de doutor em Filosofia na Universidade de Altdorf com a tese Ars combinatória (A arte da combinação), uma tentativa de criar um método universal de raciocínio, através de uma espécie de cálculo, numa antecipação da Álgebra de Boole do século $XIX$. Mas sua formação matemática ainda era precária, como ele próprio reconheceria futuramente.
Esta tese valeu um convite para ser professor de Direito na própria Universidade de Altdorf. Mas sua aspiração era a carreira pública diplomática, que efetivamente veio a exercer por toda a vida, os últimos $40$ anos junto à corte de Hanover.
A primeira missão diplomática de Leibniz no exterior, que acabou se estendendo de $1672$ a $1676$, em Paris, se politicamente não deixou marcas, no campo da matemática foi da mais alta importância. Dois fatores, principalmente, pesaram muito nesse sentido: a amizade que Leibniz travou com Huygens, que na época morava em Paris e se tornou seu orientador em matemática; e uma viagem que fez a Londres em $1673$, na qual tomou conhecimento da obra de Barrow e, talvez, da primeira versão do cálculo de Newton (aí o embrião da futura controvérsia). Numa segunda ida a Londres em $1676$, Leibniz já desenvolvera os principais aspectos e notações do seu cálculo.
Se para Newton a ideia central do cálculo era a de taxa de variação (velocidade), para Leibniz era a de diferencial. Embora sem dar uma definição precisa (nem havia como), diferencial para Leibniz era uma diferença entre dois valores infinitamente próximos de uma variável. Muito mais preocupado do que Newton com simbologia, fórmulas e regras, Leibniz acabou optando pela notação $dx$, $dy$, $\cdots$ para as diferenciais de $x$, $y$, $\cdots$, respectivamente. E num artigo de $1682$ estabeleceu regras como:
\begin{gather}
da=a, \quad \text{se}\ a\ \text{é constante}\\
d(u+v)=du+dv\\
d(uv) = udv+vdu
\end{gather}
Na dedução de $(3)$ desprezou $(du)(dv)$ (sempre procedia assim com produtos de diferenciais)

Seu cálculo integral foi explicado noutro artigo, dois anos depois. A relação deste com o cálculo diferencial, cerne da questão, é focalizada em termos de somatórios de áreas infinitesimais. Cada uma destas sob a curva $y = y(x)$ é dada por é dada por $y\ dx$. Para a soma de todas inventou o símbolo $\displaystyle \int$ (um $S$ alongado). Logo a área total sob a curva $y = y(x)$ é:
\begin{equation}
\int y\ dx
\end{equation}
Sendo a $\text{Área} (OCD) - \text{Área} (OAB) = y\ dx$ a diferencial da área, então:
\begin{equation}
d\int y\ dx = y\ dx
\end{equation}
O que mostra a invertibilidade de $d$ e $\displaystyle \int$.
Hoje não há dúvidas de que Newton e Leibniz seguiram linhas diferentes na criação do cálculo. Mas o segundo levou a pior na polêmica entre ambos, o que contribuiu para que tivesse um fim obscuro. O que diria Voltaire se assistisse ao enterro de Leibniz, no qual o único acompanhante era o fiel secretário do falecido?
Veja mais:
O Cálculo IntegralMétodo de Integração por Partes
O Cálculo de Leibniz Parte 1, Parte 2 e Parte 3 no Blog Fatos Matemáticos

- Leibniz
O matemático e filósofo alemão Gottfried Wilhelm von Leibniz, nasceu em 1º de julho de 1646, e morreu em 14 de novembro de 1716. Foi um gênio universal e um fundador de ciência moderna. Ele antecipou o desenvolvimento de lógica simbólica...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Teste Da Integral Para Convergência De Séries
O teorema conhecido como teste da integral (ou teste de Leibniz) para verificar convergências de séries, faz uso da teoria de integrais impróprias. Teorema $1$:Se $f(n)$ representa o termo geral $u_n$ de uma série numérica infinita de termos positivos,...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
- O Cálculo Integral: O Cálculo Da Áreas
A busca de processos exatos ou mesmo aproximados para o cálculo de área $S$ da região limitada por uma curva fechada deu a Arquimedes (século $IIIa.C.$ aproximadamente) a glória de ser considerado um dos maiores matemáticos de todos os tempos. Com...
