Matemática
Depois de uma longa interrupção, retornamos com mais problemas!
1 - (Putnam) Seja f polinômio em Z[x], e defina
,
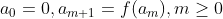
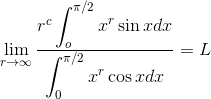
- Matemática Através De Problemas - Vi
Oi, pessoal! Dada a falta de tempo dos administradores do blog, não estamos conseguindo postar muito conteúdo. Para compensar a falta de material novo, apresentamos aqui mais uma leva de problemas interessantes: 1 - Ache todas as funções contínuas...
- Matemática Através De Problemas - Iv
Trazemos aqui mais uma seção de problemas interessantes: 1 - Seja f uma função real duas vezes diferenciável tal que, para todo x real, vale que Onde g é uma função mensurável e positiva. Prove que f é limitada. ...
- Matemática Através De Problemas - Ii
Oi, pessoal. Como prometido, vamos mostrar aqui mais alguns problemas interessantes. Relembrando que, aos interessados em ver ou enviar soluções dos problemas anteriores, nos mandem uma mensagem no e-mail [email protected] Problema...
- Matemática Através De Problemas - I
Oi, pessoal! Pra quem acompanha o blog com certa frequência, sabe que tínhamos, antes da paralisação da atividade, uma Seção de Problemas, onde postávamos problemas separados pela área olímpica da qual pertenceriam. Desse modo, não postávamos...
- Transformações Lineares Em Espaços De Dimensão Infinita - Parte I
Hoje vamos falar de Transformações Lineares, com um foco específico nas transformações onde o espaço domínio (aqui sempre tratado como E) tem dimensão infinita. Um espaço vetorial nada mais é que um conjunto fechado por somas e por multiplicação...
Matemática
Matemática Através de Problemas - III
Depois de uma longa interrupção, retornamos com mais problemas!
1 - (Putnam) Seja f polinômio em Z[x], e defina
Mostre que, se existir k tal que
2 - (Putnam) Seja P um poliedro. Mostre que existe uma constante C(P) > 0 tal que, se uma coleção de n bolas, cuja soma dos volumes é V, cobre a superfície de P, então
3 - Chamamos uma sequência crescente de números reais positivos 
de sequência limite absoluto se, dado um intervalo [a,b] e uma função f contínua tal que existe um intervalo [c,d] com a < c < d < b com
Então o limite
Existe e é finito.
Mostre que uma sequência crescente de reais positivos é sequência limite absoluto se, e só se, o limite
Mostre que uma sequência crescente de reais positivos é sequência limite absoluto se, e só se, o limite
Existe e é finito.
4 - (Putnam) Seja f : R -> R função contínua tal que
Prove que f = 0 em [-1,1].
5 - (Putnam) Encontre c, L tais que
~ Dicas e Soluções Parciais ~
1 - Use que, se P tem coeficientes inteiros e a,b são inteiros distintos, então
Utilize tal propriedade repetidas vezes.
2 - Considere uma face de P, veja qual a área máxima que a interseção de uma bola com uma tal face pode ser, e então use uma desigualdade entre as médias de ordem 2 e 3 para concluir.
3 - Use uma desigualdade de Hölder na integral do denominador, com expoente 
. Note que, se
Para terminar, mostre que a propriedade desejada é equivalente a
Existir e ser finito
4 - Mostre que f (0) = 0, escreva 
, e itere o processo. Você pode precisar provar que vale primeiro para x da forma 
, e usar um argumento de densidade.
5 - Calcule a integral de cima por partes. c = - 1 deve funcionar. Para achar L apropriado, separe a integral entre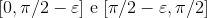 
, e faça algumas estimativas. Talvez mudar coordenadas seja interessante.
- Matemática Através De Problemas - Vi
Oi, pessoal! Dada a falta de tempo dos administradores do blog, não estamos conseguindo postar muito conteúdo. Para compensar a falta de material novo, apresentamos aqui mais uma leva de problemas interessantes: 1 - Ache todas as funções contínuas...
- Matemática Através De Problemas - Iv
Trazemos aqui mais uma seção de problemas interessantes: 1 - Seja f uma função real duas vezes diferenciável tal que, para todo x real, vale que Onde g é uma função mensurável e positiva. Prove que f é limitada. ...
- Matemática Através De Problemas - Ii
Oi, pessoal. Como prometido, vamos mostrar aqui mais alguns problemas interessantes. Relembrando que, aos interessados em ver ou enviar soluções dos problemas anteriores, nos mandem uma mensagem no e-mail [email protected] Problema...
- Matemática Através De Problemas - I
Oi, pessoal! Pra quem acompanha o blog com certa frequência, sabe que tínhamos, antes da paralisação da atividade, uma Seção de Problemas, onde postávamos problemas separados pela área olímpica da qual pertenceriam. Desse modo, não postávamos...
- Transformações Lineares Em Espaços De Dimensão Infinita - Parte I
Hoje vamos falar de Transformações Lineares, com um foco específico nas transformações onde o espaço domínio (aqui sempre tratado como E) tem dimensão infinita. Um espaço vetorial nada mais é que um conjunto fechado por somas e por multiplicação...