Matemática
***

- Post Sexcentésimo Sexagésimo Sexto
?Aqui há sabedoria. Aquele que tem entendimento, calcule o número da besta; porque é o número de um homem, e o seu número é seiscentos e sessenta e seis.? Apocalipse 13:18 O livro das Revelações no Novo Testamento apresenta um número que causa...
- Bruxaria Matemática: Elevado Ao Quadrado
Poliedro e Belinha estão resolvendo questões de potência: *** A situação descrita acima foi baseada nesta tirinha meme: Na realidade o Poliedro não esta realizando nenhum truque. Não é tão complicado de provar que este processo...
- Supremo Quadrado Mágico Pitagórico
O triângulo da Figura 1 é um triângulo retângulo, desta forma podemos aplicar o Teorema de Pitágoras. Figura 1: Quadrado Mágico Pitagórico Se você examinar a Figura 1 com o devido cuidado verá que temos três quadrados mágicos, onde...
- O Quadrado Mágico Da Hipotenusa De Um Triângulo Retângulo
O grande Pitágoras de Samos cometeu um grande erro ao formular seu famoso teorema: ele não levou em conta que algum dia o triângulo retângulo poderia cair em mãos de um MateMágico!! Segundo seu teorema: o quadrado da Hipotenusa é igual à soma...
- Curiosidade
Se você somar 1 ao produto de quatro números inteiros consecutivos, o resultado sempre será um quadrado perfeito. Em outros termos, o que devemos demonstrar é: Dado um número x inteiro qualquer o resultado da operação R = x(x + 1)(x + 2)(x + 3)...
Matemática
NewMerologia
Lee Sallows é um matemático especialista em quadrados mágicos e sugeriu um método baseado em palavras que denotam números denominado ?NewMerologia? (?new merology?, em inglês) para substituir o tradicional método de gematria que relaciona números a nomes.
A gematria define como A = 1, B = 2, C = 3 até Z = 26 na sequência soma-se todos os valores correspondentes as letras do nome.
Observe por exemplo o número 1 que em inglês é ONE em gematria temos: 15 + 14 + 5 = 34. Mas o número que corresponde a ONE deveria ser 1.
Os raros números em que seu total na gematria é igual ao seu valor numérico são chamados números perfeitos. Em inglês não apresenta nenhum número que na gematria seja perfeito.
Sallows se perguntou o que ocorreria se associarmos um número inteiro a cada letra, de modo que a maior quantidade possível dos numerais ONE, TWO, etc ... sejam perfeitos.
Para tornar o problema mais interessante, letras diferentes devem ter valores diferentes. E assim, obtemos uma série de equações como:
O + N + E = 1
T + W + O = 2
T + H + R + E + E = 3
As variáveis algébricas O, N, E, T, W, H, R, ... que devemos considerar como números inteiros, todos diferentes.
Iniciamos supondo que E = 1 e N = 2, então em O + N + E = 1, obtemos O = ?2. Continuando o raciocínio e aplicando os valores encontrados determinamos os valores para as demais letras para resolução: em N + I + N + E = 9, obtemos I = 4; para T + E + N = 10, obtemos T = 7; para T + W + O = 2, obtemos W = ?2.
Em T + H + R + E + E = 3 temos uma nova situação onde temos que considerar H = 3 e obtemos R = ?9; em F + O + U + R = 4 considerando F = 5, obtemos U = 10.
Agora obtemos V = ?5, em F + I + V + E = 5. Em S + I + X = 6 para obter o valor de X devemos antes resolver S + E + V + E + N = 7, obtendo S = 8 e X = ?6.
Para completar a perfeição de ONE a TEN resta apenas E + I + G + H + T = 8, obtendo G = ?7.
O problema esta em começar a considerar os valores iniciais de algumas de algumas das letras.
No nosso caso ao considerar E = 1 e N = 2, não conseguimos deixar perfeito o numero zero. Z + E + R + O = 0, obtemos Z = 10, ou seja, Z = U = 10 violando a regra em que as letras devem ter valores diferentes.
Lee Sallows também aplicou a Newmerologiaem seus quadrados mágicos, inventando um truque bem interessante.
Escolha qualquer número do quadrado mágico a seguir.
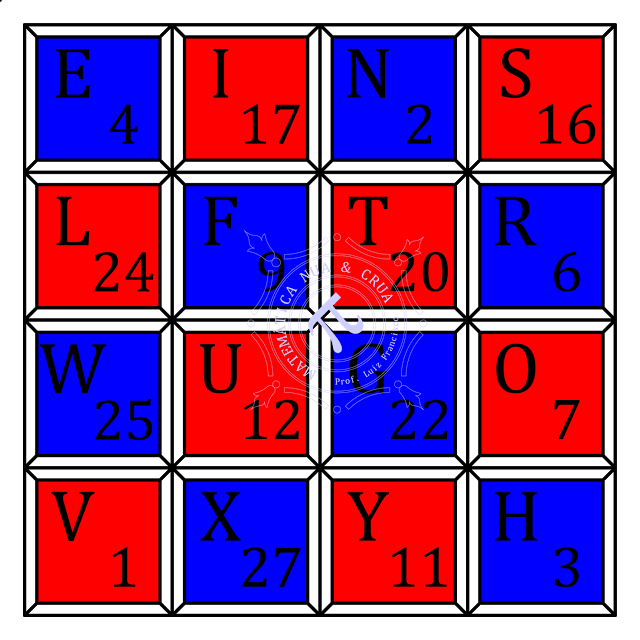 |
| Quadrado Mágico de Lee Sallows |
Soletre o número escolhido em inglês, letra por letra. Realize um soma aritmética com os números correspondentes a cada letra no quadro. As letras nos quadrados azuis devem ser subtraídos e os números das casas vermelhas devem ser somados. O resultado será mais ou menos o número que você escolheu.
Por exemplo: 22 ? TWENTY ? TWO: T + W + E + N + T + Y + T + W + O
20 ? 25 ? 4 ? 2 + 20 ? 25 + 7 = 22
Temos uma boa oportunidade de realizar uma atividade em sala de aula unindo o ensino da matemática com o ensino do idioma inglês.
Para aqueles que tem dificuldades em lembrar dos números em inglês temos:
1 ? ONE
2 ? TWO
3 ? THREE
4 ? FOUR
6 ? SIX
7 ? SEVEN
9 ? NINE
11 ? ELEVEN
12 ? TWELVE
16 ? SIXTEEN
17 ? SEVENTEEN
20 ? TWENTY
22 ? TWENTY?TWO
24 ? TWENTY?FOUR
25 ? TWENTY?FIVE
27 ? TWENTY?SEVEN
Fonte:STEWART, Ian. Almanaque das Curiosidades Matemáticas. Rio de Janeiro: Zahar, 2.009.
 Professor compartilhe sua criatividade! |  Compartilhe esta ideia de divulgar a Matemática! |

- Post Sexcentésimo Sexagésimo Sexto
?Aqui há sabedoria. Aquele que tem entendimento, calcule o número da besta; porque é o número de um homem, e o seu número é seiscentos e sessenta e seis.? Apocalipse 13:18 O livro das Revelações no Novo Testamento apresenta um número que causa...
- Bruxaria Matemática: Elevado Ao Quadrado
Poliedro e Belinha estão resolvendo questões de potência: *** A situação descrita acima foi baseada nesta tirinha meme: Na realidade o Poliedro não esta realizando nenhum truque. Não é tão complicado de provar que este processo...
- Supremo Quadrado Mágico Pitagórico
O triângulo da Figura 1 é um triângulo retângulo, desta forma podemos aplicar o Teorema de Pitágoras. Figura 1: Quadrado Mágico Pitagórico Se você examinar a Figura 1 com o devido cuidado verá que temos três quadrados mágicos, onde...
- O Quadrado Mágico Da Hipotenusa De Um Triângulo Retângulo
O grande Pitágoras de Samos cometeu um grande erro ao formular seu famoso teorema: ele não levou em conta que algum dia o triângulo retângulo poderia cair em mãos de um MateMágico!! Segundo seu teorema: o quadrado da Hipotenusa é igual à soma...
- Curiosidade
Se você somar 1 ao produto de quatro números inteiros consecutivos, o resultado sempre será um quadrado perfeito. Em outros termos, o que devemos demonstrar é: Dado um número x inteiro qualquer o resultado da operação R = x(x + 1)(x + 2)(x + 3)...
