Matemática

O Plano no Espaço Tridimensional

Por Profº Paulo Sérgio - Blog Fatos Matemáticos

O estudo do plano é importante no estudo das funções de duas váriaveis. O conceito de plano tangente a superfície está intimamente relacionado ao conceito de derivada e diferenciabilidade destas funções. Portanto, o estudo desta classe de superfícies é o primeiro passo para compreender o Cálculo de funções de várias variáveis.

Uma das formas clássicas de obter a equação de um plano $[;\alpha;]$ no $[;\mathbb{R}^3;]$ é através de um vetor normal (ortogonal) $[;\vec{N} = (a,b,c);]$ a $[;\alpha;]$ e de um ponto [;P_0(x_0,y_0,z_0);]

sobre este plano conforme a figura acima.

é um ponto qualquer sobre $[;\alpha;]$ , então $[;\vec{N} \perp \vec{P_0P};]$ , de modo que

$[;\vec{N}\cdot \vec{P_0P} = 0 \quad \Rightarrow \quad (a,b,c)\cdot (x - x_0,y - y_0,z - z_0) = 0;]$

$[; a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 \quad \Rightarrow;]$

Denotando por [;d = -ax_0 -by_0 - cz_0;]

, obtemos a equação cartesiana ou geral do plano $[;\alpha;]$ , isto é,

$[;\alpha: \quad ax + by + cz + d = 0 \qquad (1);]$

Observe que os coeficientes [;a;]

de $[;x\ ;]$ , [;y;]

são as componentes do vetor normal $[;\vec{N};]$ .

Exemplo 1: Determine a equação geral do plano que passa pelos pontos

Resolução: Sejam os vetores $[;\vec{AB} = B - A = (2,0,3) - (-1,2,1) = (3,-2,4);]$ e $[;\vec{AC} = C - A = (1,3,2) - (-1,2,1) = (2,1,1);]$ . Como esses vetores pertencem ao plano, então o vetor normal é dado por;

$[;\vec{N} = \vec{AB}\times \vec{AC} = (-6,5,7);]$

Assim, segue da equação [;(1);]

, que o plano procurado $[;\alpha;]$ é [;-6x + 5y + 7z + d = 0;]

. Para determinar [;d;]

, subtituímos as coordenadas de quaisquer um dos pontos acima. Por exemplo, para o ponto [;A(-1,2,1);]

, temos:

$[;-6\cdot (-1) + 5\cdot 2 + 7\cdot 1 + d = 0 \quad \Rightarrow \quad d = -23;]$

Logo,

$[;\alpha: \ -6x + 5y + 7z - 23 = 0;]$

é a equação do plano procurado.

Conforme as componentes do vetor normal a um plano é nula, obtemos planos paralelos aos eixos coordenados ou planos paralelos aos planos coordenados se duas componentes são nulas.

Se apenas uma das componentes do vetor normal $[;\vec{N};]$ ao plano $[;\alpha;]$ é nula, por exemplo, [;c = 0;]

, é fácil ver que este plano é paralelo ao eixo [;z;]

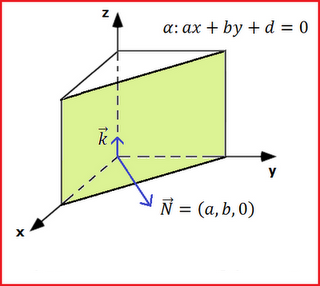
De fato, sendo $[;\vec{N} = (a,b,0);]$ então $[;\vec{N} \in x0y;]$ de modo que $[;\vec{N} \perp Oz;]$ e por definição de vetor normal, segue que $[;\alpha \ \parallel \ 0z;]$ , conforme a figura abaixo.

Neste caso, a sua equação cartesiana é dada por $[;\alpha: \quad ax + by + d = 0;]$ . De forma análoga, um plano paralelo ao eixo $[;x\ ;]$ é dado por $[;\beta: \ by + cz + d = 0;]$ e um plano paralelo ao eixo [;y;]

é dado por $[;\gamma:\ ax + cz + d = 0;]$ .

Temos também que se um plano é paralelo ao plano [;xOy;]

, então sua equação geral é dada por $[;\alpha\ cz + d = 0;]$ . De fato, neste caso,

$[;\vec{N} \parallel \vec{k} \quad \Rightarrow \quad a = b = 0;]$

Os outros casos são análogos.

Exemplo 2: Determine a equação geral do plano paralelo ao eixo [;z;]

e que passa pelos pontos [;(2,0,0);]

paralelo ao eixo [;z;]

.

Resolução: Usando expressão $[; \alpha: \ ax + by + d = 0;]$ , para o ponto [;(2,0,0);]

temos

$[;2\cdot a + b\cdot 0 + d = 0 \quad \Rightarrow \quad d = -2a;]$

e para o ponto [;(1,1,0);]

, obtemos

$[;1\cdot a + 1\cdot b -2a = 0 \quad \Rightarrow \quad b = a;]$

Logo,

$[;\alpha:\ ax + ay - 2a = 0 \quad \text{ou} \quad x + y - 2 = 0;]$

- Plano Cartesiano
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...

- Equação Geral Da Reta No Plano
Equação Geral da Reta no PlanoMarcos Noé Reta no planoAs equações na forma ax + by + c = 0 são expressões representativas de retas do plano. Os coeficientes a, b e c são números reais constantes, considerando a e b valores...

- Geometria Analítica, Parábola
1 - Introdução Se você consultar o Novo Dicionário Brasileiro Melhoramentos - 7ª edição, obterá a seguinte definição para a parábola: "Curva plana, cujos pontos são eqüidistantes de um ponto fixo (foco) e de uma reta fixa (diretriz) ou curva...

- Projeção Ortogonal De Um Segmento De Reta Sobre Um Plano
$1)$ Projeção de um ponto Definição $1$: Chama-se projeção ortogonal de um ponto $P$ sobre um plano $\alpha$ o pé da perpendicular ao plano conduzida pelo ponto. O plano $\alpha$ é chamado de plano de projeção e a reta perpendicular é chamada...

- Distância Entre Dois Pontos No Plano
Nesta postagem, veremos como determinar a distância entre dois pontos distintos no plano cartesiano. Definição: Sejam dois pontos distintos $A(x_A,y_A)$ e $B(x_B,y_B)$ no plano cartesiano. Distância é a medida do segmento de reta que tem os pontos...

Matemática