Matemática
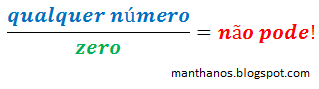Este é outro fato que, apesar de ser muito conhecido, dificilmente encontramos um indivíduo que o saiba esclarecer. Esta postagem tentará então explicá-lo.
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Solução Do Problema Dos Ovos De Páscoa.
[veja o problema aqui] Vamos à explicação: Inicialmente observe a soma de algumas frações: 1/2 + 1/2 = 2/2 = 1O fato de a soma acima totalizar 1 significa que se você for dividir uma quantidade qualquer entre duas pessoas, de modo que uma fique...
- Por Que Todo Número Elevado A Zero Dá Um?
Inicialmente esclareço que a finalidade desta postagem é responder por que todo número, diferente de zero, elevado a zero é igual a um?. A importante restrição diferente de zero não foi mencionada no título para não estendê-lo demais. Resposta...
- Equação De 2º Grau
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:a) x² + 9 x + 8 = 0 (R:-1 e -8) b) 9 x² - 24 x + 16 = 0 (R:4/3) c) x² - 2 x...
Matemática
Por que não existe divisão por zero?
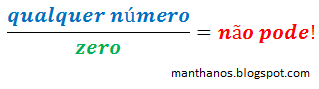
Primeiramente vamos relembrar o que significa dividir:
Sejam a e b números reais quaisquer.
Dividir a por b significa achar um número c tal que b.c = a:
Assim, por exemplo, dividir 32 por 4 significa achar um número c tal que 4.c = 32:
No caso acima, c = 8.
Deste modo, se queremos dividir o número a por 0, temos que achar um número c tal que 0.c = a:
Observe que não importa qual seja o valor escolhido para c, o produto 0.c será sempre igual a 0 e nunca igual a a, logo é impossível dividir a por 0 (pois não existe c tal que 0.c = a, desde que a seja diferente de zero).
Observe que no caso em que a = 0 (zero dividido por zero) teremos uma expressão indeterminada, pois se quisermos efetuar tal divisão teremos que encontrar c, tal que 0.c = 0:
Pergunta: Qual é o valor que deve assumir c para cumprir a condição acima?
Resposta: Qualquer um! Você pode escolher c = 1 ou c = 17 ou c = 19586, (de um modo mais geral você pode pôr c = qualquer número real), logo a divisão por zero não está bem definida (pois há mais de um valor para c que cumpre a condição).
Vamos aproveitar e explicar também porque zero dividido por qualquer número é zero:
De acordo com o significado da divisão acima expresso, dividir o número 0 por b significa achar um número c tal que b.c = 0:
Observe que, para qualquer que seja o número b teremos, necessariamente, que escolher c = 0. Por isso zero dividido por qualquer número é zero (pois se queremos um produto que resulte em zero, um dos fatores deverá ser zero, mas estamos excluindo a possibilidade de ser b = 0, pois já mostramos que se o denominador é zero então a divisão não existe, logo nos resta pôr c = 0 independentemente dos possíveis valorer de b).
Referência:
LIMA, Elon Lages. Meu Professor de matemática e Outras Histórias, Sociedade Brasileira de Matemática, 1991.
*Erros podem ser apontados aqui.
_______________________________________________________
FIQUE SABENDO OUTROS PORQUÊS:
Por que racionalizar o denominador?
Por que menos vezes menos dá mais?
Por que fatorial de zero é um?
_______________________________________________________
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Solução Do Problema Dos Ovos De Páscoa.
[veja o problema aqui] Vamos à explicação: Inicialmente observe a soma de algumas frações: 1/2 + 1/2 = 2/2 = 1O fato de a soma acima totalizar 1 significa que se você for dividir uma quantidade qualquer entre duas pessoas, de modo que uma fique...
- Por Que Todo Número Elevado A Zero Dá Um?
Inicialmente esclareço que a finalidade desta postagem é responder por que todo número, diferente de zero, elevado a zero é igual a um?. A importante restrição diferente de zero não foi mencionada no título para não estendê-lo demais. Resposta...
- Equação De 2º Grau
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:a) x² + 9 x + 8 = 0 (R:-1 e -8) b) 9 x² - 24 x + 16 = 0 (R:4/3) c) x² - 2 x...