Matemática
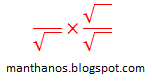
Uma prática comum a todo usuário de matemática (ao menos a boa parte deles) é racionalizar o denominador. Por exemplo, ao se depararem com uma fração do tipo
^{2}}=\frac{\sqrt{2}}{2} "\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\cdot1=\frac{1}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{\sqrt{2}}{\left (\sqrt{2} \right )^{2}}=\frac{\sqrt{2}}{2}")
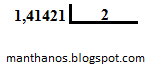
ou equivalentemente
Agora se você optou por deixar raiz de dois no divisor terá que efetuar
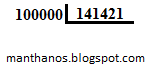
- Por Que Não Existe Divisão Por Zero?
Este é outro fato que, apesar de ser muito conhecido, dificilmente encontramos um indivíduo que o saiba esclarecer. Esta postagem tentará então explicá-lo. Primeiramente vamos relembrar o que significa dividir: Sejam a e b números reais quaisquer....
- Por Que Todo Número Elevado A Zero Dá Um?
Inicialmente esclareço que a finalidade desta postagem é responder por que todo número, diferente de zero, elevado a zero é igual a um?. A importante restrição diferente de zero não foi mencionada no título para não estendê-lo demais. Resposta...
- Por Que "menos Vezes Menos Dá Mais"?
As pessoas sabem desde muito cedo (talvez desde o fundamental) que as regras de sinais para a multiplicação podem ser representadas por algo como uma tabelinha: + + = +- - = ++ - = -- + = - Se alguma das regras acima pode causar perplexidade é a segunda:...
- Fração
Frações de frações Definição: Fração de fração é uma ou mais partes de uma fração Regra - Para se calcular uma fração, basta fazer a multiplicação das frações. Redução de fração Reduzir inteiros a fração imprópria Regra – Para...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...
Matemática
Por que racionalizar o denominador?
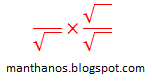
Uma prática comum a todo usuário de matemática (ao menos a boa parte deles) é racionalizar o denominador. Por exemplo, ao se depararem com uma fração do tipo
é comum adotarem o seguinte procedimento:
O que certamente é menos comum é encontrarmos um indivíduo que saiba explicar o motivo de se fazer isso (ainda que execute perfeitamente o procedimento). Possivelmente ele dirá que foi ensinado deste modo.
Esta postagem se dedica então a justificar a ação de racionalizar os denominadores de simples frações numéricas, tais quais a do exemplo acima.
A explicação é bastante singela, e é possível apresentar dois argumentos:
Em primeiro lugar há quem diga que a fração fica mais bonita com o denominador racionalizado. Será mesmo?!
De qualquer modo há um argumento bem melhor: o costume de racionalizar os denominadores das frações remonta a época em que não existia calculadoras, ou seja, era uma questão operacional; de fato, a racionalização facilita os cálculos manuais.
Voltando ao nosso exemplo, realmente nos parece mais fácil efetuar
em vez de efetuar
Além disso, se você quiser obter mais casas decimais exatas, no primeiro caso o trabalho não será perdido já no segundo caso você terá que refazer a conta toda.
Na prática, se fossemos resolver a conta acima, de acordo com o processo que já estamos acostumados, efetuaríamos a seguinte operação:
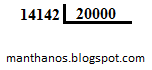
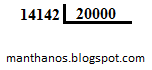
Supõe então que você efetue a divisão mas verifique que necessita de mais exatidão, ou seja, você precisa do seguinte resultado:
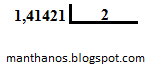
ou equivalentemente
Observe que o trabalho que você teve na conta anterior não seria perdido, ele poderia ser aproveitado:
Agora se você optou por deixar raiz de dois no divisor terá que efetuar
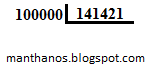
que dará muito mais trabalho, pois ainda que as primeiras casas do quociente sejam as mesmas os restos serão diferentes e deverão ser recalculados e, portanto, neste sentido o trabalho não será aproveitado.
Deste modo, atualmente não há a mínima necessidade de racionalizar o denominador visto que os cálculos podem ser efetuados nas calculadoras. Contudo este costume está de tal modo incrustado nos indivíduos que dificilmente encontramos (se é que encontramos) um livro que não traga a resposta racionalizada, logo o procedimento não pode ser ignorado e os alunos devem aprendê-lo. Mas isto também não é motivo para o professor marcar como errada uma questão em alguma prova só porque o aluno deixou de racionalizar (a menos, é claro, que o enunciado diga explicitamente que é para racionalizar).
Observação: acima representamos uma conta cujo divisor é 200000 e cujo dividendo é 141421 afirmando que ela é mais simples que a outra. Observe que para dividir por 200000 basta dividir por 2 e então deslocar a vírgula cinco casas para a esquerda. Isso significa que realmente esta divisão é mais fácil de ser realizada do que a outra.
(Eu particularmente gosto de racionalizar, e pretendo continuar racionalizando. Deixe sua opinião nos comentários ou outra justificativa caso conheça alguma).
Que fique claro então que não é errado deixar de racionalizar o denominador.
Que fique claro então que não é errado deixar de racionalizar o denominador.
Referências:
LIMA, Elon Lages; WAGNER, Eduardo. et al. Perguntas e Respostas - Seção 1. Rio de Janeiro: IMPA (Instituto Nacional de Matemática Pura e Aplicada), 2010. PAPEM (Programa de Aperfeiçoamento de Professores de Matemática do Ensino Médio). Vídeoaula disponível para download em: <http://video.impa.br/index.php?page=janeiro-de-2010>.
*Erros podem ser apontados aqui.
_______________________________________________________
FIQUE SABENDO OUTROS PORQUÊS:
Por que todo número elevado a zero dá um?
Por que menos vezes menos dá mais?
_______________________________________________________
- Por Que Não Existe Divisão Por Zero?
Este é outro fato que, apesar de ser muito conhecido, dificilmente encontramos um indivíduo que o saiba esclarecer. Esta postagem tentará então explicá-lo. Primeiramente vamos relembrar o que significa dividir: Sejam a e b números reais quaisquer....
- Por Que Todo Número Elevado A Zero Dá Um?
Inicialmente esclareço que a finalidade desta postagem é responder por que todo número, diferente de zero, elevado a zero é igual a um?. A importante restrição diferente de zero não foi mencionada no título para não estendê-lo demais. Resposta...
- Por Que "menos Vezes Menos Dá Mais"?
As pessoas sabem desde muito cedo (talvez desde o fundamental) que as regras de sinais para a multiplicação podem ser representadas por algo como uma tabelinha: + + = +- - = ++ - = -- + = - Se alguma das regras acima pode causar perplexidade é a segunda:...
- Fração
Frações de frações Definição: Fração de fração é uma ou mais partes de uma fração Regra - Para se calcular uma fração, basta fazer a multiplicação das frações. Redução de fração Reduzir inteiros a fração imprópria Regra – Para...
- Números Decimais
NÚMEROS DECIMAIS FRAÇÃO DECIMAL Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100... como: a) 7/10 b) 3/100 c) 27/1000 NÚMEROS DECIMAIS a) 7/10 = 0,7 b) 3/100 = 0,03 c) 27/1000 = 0,027 nos números decimais...