Matemática
 Considere as informações para responder às questões de números 31 e 32.
Considere as informações para responder às questões de números 31 e 32.
***

- Questão 21 E 22 ? Vestibulinho Etec ? 2° Semestre De 2.014
Considere as informações para responder às questões de números 21 e 22. Um técnico em móveis projetou uma estante conforme a figura 1. A figura 2 apresenta o esquema da parte frontal da estante. No esquema da figura 2, tem-se que: D é ponto...
- Questão 44 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Para determinar a altura de um prédio, um estudante, que estava sem instrumento de medida de comprimento, e com ajuda de um instrumento que ele construiu, mediu de forma aproximada o ângulo de elevação do prédio a partir de A, obtendo 45°. Em seguida,...
- Questão 36 ? Formação Básica Do Professor E Formação Específica Do Professor ? 2.007 ? Estado De São Paulo
Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfí-cie. Na figura, os ângulos ABC e BCD medem, respectiva-mente, 90º...
- Sistema Solar
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Aceleração Centrípeta
No movimento circular, a partícula tem a direção da velocidade linear constantemente alterada. Isto ocorre porque sobre ela, atua uma aceleração chamada de Aceleração Centrípeta Considerando o caso de um satélite que orbita em torno da Terra....
Matemática
Questão 31 e 32 ? Vestibulinho Etec ? Centro Paula Souza ? 1° Semestre de 2.013
As órbitas dos satélites de comunicação são geoestacionárias e devem ser equatoriais, isto é, estar no plano da linha do Equador terrestre.
Como o nome sugere, um satélite geoestacionário (geo = Terra, estacionário = parado) deve acompanhar a rotação do planeta de forma a car sempre parado em relação a um ponto fixo na superfície da Terra.
A Figura 1 ilustra a ideia do ?campo de visão? de um satélite geoestacionário, ou seja, mostra a região do planeta que o satélite é capaz de cobrir, ?enxergar?.
O satélite envia sinais eletromagnéticos para a Terra, e o que delimita a região coberta pelos sinais é o fato de o planeta ser esférico. Desta forma, os sinais recebidos ou transmitidos, entre o satélite e a Terra, ficam confinados num cone cuja intersecção com a superfície da Terra determina a área de cobertura do satélite.
É nesta região da superfície da Terra que podemos colocar antenas capazes de trocar sinais eletromagnéticos com o satélite.
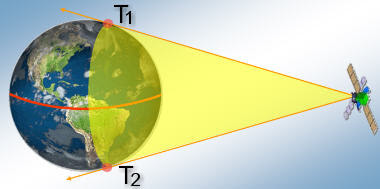 |
| Figura 1 |
No exemplo da Figura 1, os sinais emitidos pelo satélite, no limite, ?tocam? o planeta nos pontos T1 e T2.
Na Figura 2, apresenta-se um modelo matemático simplificado da posição do satélite S em relação à Terra.
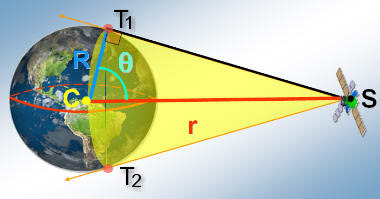 |
| Figura 2 |
Na Figura 2, temos:
- Ponto S: satélite (considerado como um ponto no espaço).
- As semirretas ST1 e ST2 tangentes à superfície da Terra nos pontos T1 e T2, respectivamente.
- Ponto C: centro da Terra e da órbita do satélite S.
- Quadrilátero ST1CT2: figura plana.
- R: medida do raio da Terra.
- r: medida do raio da órbita do satélite S.
- ?: medida do ângulo SCT1.
Note que ? corresponde à latitude máxima que o sinal do satélite pode alcançar.
Considerando os valores aproximados de 6400 km para o raio da Terra e 42000 km para o raio da órbita do satélite geoestacionário S, determina-se que ?= 81,2°.
Conclusão: um satélite geoestacionário cobre uma região entre as latitudes 81,2° N e 81,2° S.
Essa região não chega aos polos geográficos da Terra. Mas chega quase lá. E isso não é nenhum problema porque ninguém, aparentemente, vai querer transmitir sinais de TV ou internet para ursos polares ou pinguins, vai?!
(fisicamoderna.blog.uol.com.br/arch2008-03-16_2008-03-22.html Acesso em: 12.08.2012. Adaptado)
***
Questão 31
De acordo com o texto, conclui-se que a medida do ângulo T1ST2 é
(A) 8,8°.
(B) 13,2°.
(C) 17,6°.
(D) 22,0°.
(E) 26,4°.
Solução: (C)
Segundo a Figura 2 os triângulos ST1C e ST2C são congruentes (iguais).
O ângulo T1ST2 é a soma do ângulo T1SC e do ângulo T2SC.
Sabemos que a soma dos ângulos internos de um triângulo é sempre 180°.
No triângulo ST1C, temos dois ângulos indicados ? = 81,2° e 90°, então:
T1SC + 90° + 81,2° = 180°
T1SC = 180° ? 90° ? 81,2° = 8,8°
Então T1SC = T2SC = 8,8°:
T1ST2 = T1SC + T2SC = 8,8° + 8,8° = 17,6°
***
Questão 32
Considerando uma estação receptora no ponto T1, a distância de T1 a S é, Em quilômetros, aproximadamente,
Admita que a altura da estação receptora é desprezível em relação ao raio da Terra e em relação à distância do satélite até o centro da Terra.
Adote: ?172304 = 415
(A) 4,15 · 101.
(B) 4,15 · 102.
(C) 4,15 · 103.
(D) 4,15 · 104.
(E) 4,15 · 105.
Solução: (D)
O triângulo ST1C é retângulo no ponto T1, ou seja, no ponto T1 temos um ângulo de 90°.
Segundo o texto e a Figura 2, temos:
- T1C é igual ao raio da Terra que mede 6400 km, e que T1C é um dos catetos do triângulo ST1C;
- SC é igual ao raio da orbita do satélite Terra que mede 42000 km, e que SC é a hipotenusa do triângulo ST1C, e;
- T1C é outro cateto do triângulo ST1C.
Aplicando o Teorema de Pitágoras no triângulo ST1C, temos:
(SC)2 = (T1C)2 + (T1S)2
(T1S)2 = (SC)2 ? (T1C)2
(T1S) = ? [(SC)2 ? (T1C)2]
(T1S) = ? [(42000)2 ? (6400)2]
Aqui é que vai complicar muito os cálculos, pois vamos trabalhar com números grandes. Vou resolver da forma que considero mais fácil e que apresenta o menor risco de errar, mas nada impede o leitor de resolver da forma de considerar mais fácil.
Vou transformar 42000 no produto de 420 × 100 e 6400 no produto de 64 × 100. Escolhi 100 como um dos fatores para ajudar nos cálculos:
(T1S) = ? [(420 × 100)2 ? (64 × 100)2]
(T1S) = ? [(4202 × 1002) ? (642 × 1002)]
(T1S) = ? [(176400 × 10000) ? (4096 × 10000)]
(T1S) = ? [(176400 × 104) ? (4096 × 104)]
(T1S) = ? [(176400 ? 4096) × 104]
(T1S) = ? (172304 × 104)
(T1S) = ? (172304) × ?(104)
(T1S) = 415 × 102
(T1S) = 4,15 × 104
Como citei anteriormente nada impede de realizar os cálculos da seguinte forma:
(T1S) = ? [(42000)2 ? (6400)2]
(T1S) = ? [(1764000000) ? (40960000)]
(T1S) = ? (1723040000)
(T1S) = ? (172304 × 10000)
(T1S) = ? (172304 × 104)
(T1S) = ? (172304) × ?(104)
(T1S) = 415 × 102
(T1S) = 4,15 × 104
(T1S) = 4,15 × 104
 Professor compartilhe sua criatividade! |  Compartilhe esta ideia de divulgar a Matemática! |

POSTAR UM COMENTÁRIO
- Questão 21 E 22 ? Vestibulinho Etec ? 2° Semestre De 2.014
Considere as informações para responder às questões de números 21 e 22. Um técnico em móveis projetou uma estante conforme a figura 1. A figura 2 apresenta o esquema da parte frontal da estante. No esquema da figura 2, tem-se que: D é ponto...
- Questão 44 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Para determinar a altura de um prédio, um estudante, que estava sem instrumento de medida de comprimento, e com ajuda de um instrumento que ele construiu, mediu de forma aproximada o ângulo de elevação do prédio a partir de A, obtendo 45°. Em seguida,...
- Questão 36 ? Formação Básica Do Professor E Formação Específica Do Professor ? 2.007 ? Estado De São Paulo
Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfí-cie. Na figura, os ângulos ABC e BCD medem, respectiva-mente, 90º...
- Sistema Solar
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Aceleração Centrípeta
No movimento circular, a partícula tem a direção da velocidade linear constantemente alterada. Isto ocorre porque sobre ela, atua uma aceleração chamada de Aceleração Centrípeta Considerando o caso de um satélite que orbita em torno da Terra....
