Matemática

Questão 58 ? Processo de Promoção ? QM ? Professor de Matemática ? SEE/SP ? 2.015

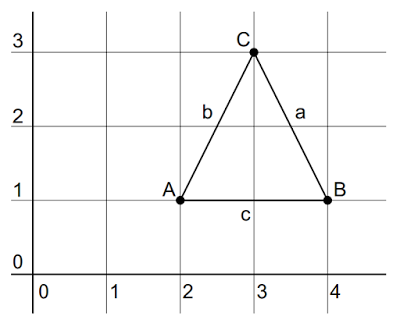
Um dos cadernos do Professor para o 3° ano do Ensino Médio, da Secretaria de Educação de São Paulo, discute algumas inovações curriculares para o ensino dos números complexos: apresenta-se, por exemplo, a correspondência das operações com números complexos com movimentos no plano de Argand Gauss.

Considere a região triangular do plano complexo, indicada na figura. Cada ponto da região é a imagem de um número complexo.

Se cada ponto dessa região triangular for multiplicada pelo número imaginário z = 2iconclui-se que a região triangular sofrerá uma rotação de

(A) 90°, correspondente a multiplicação por i, e seus lados serão ampliados por meio do fator 2, tendo sua área, portanto, duplicada.

(B) 90°, correspondente a multiplicação por i, e seus lados serão ampliados por meio do fator 2, tendo sua área, portanto, quadruplicada.

(C) 180°, correspondente a multiplicação por i, e seus lados serão ampliados por meio do fator 2, tendo sua área, portanto, duplicada.

(D) 180°, correspondente a multiplicação por i, e seus lados serão ampliados por meio do fator 2, tendo sua área, portanto, quadruplicada.

(E) 360°, correspondente a multiplicação por i, e seus lados serão ampliados por meio do fator 2, tendo sua área, portanto quadruplicada.

Solução: (B)

Segundo o Caderno do Professor 3° ano do Ensino Médio Matemática (2.014, p.85):

?(...)

quando se multiplica um número real por ?1, sua imagem na reta real é deslocada segundo um arco de 180º, passando da semirreta positiva para a negativa, e vice-versa: N · (?1) = ?N (resultado: rotação de 180º);
quando se multiplica um número real por i², ou seja, por ?1, é como se tivéssemos multiplicado o número real por i e multiplicássemos o resultado novamente por i: N · (?1) = N · i · i = ?N;
se o resultado das duas multiplicações idênticas e sucessivas foi uma rotação de 180º, seria natural considerar o resultado de cada uma das multiplicações parciais por i como o resultado de uma rotação de 90º: N · i = Ni (rotação de 90º);
assim, multiplicar um número real por i corresponderia a representar tal número em um eixo perpendicular ao eixo real.?

Segundo o Caderno do Professor 3° ano do Ensino Médio Matemática (2.014, p.96):

?d) Cada ponto da região será multiplicado pelo número real 2.

Cada ponto da região terá seu módulo multiplicado por 2; logo, a região será ampliada, tendo cada segmento multiplicado por 2, e sua área multiplicada por 4. Como as distâncias de cada ponto até a origem serão multiplicadas por 2, haverá uma translação (afastamento da origem) com a ampliação.?

Segundo o Caderno do Professor 3° ano do Ensino Médio Matemática (2.014, p.97):

?12.Considere a região do plano complexo, indicada na figura. Cada ponto da região é a imagem de um complexo e será objeto de uma transformação. Represente no plano complexo a região resultante após a multiplicação de cada ponto da região pelo imaginário i.

De maneira geral, ao multiplicar um número complexo z por i, seu módulo permanece o mesmo, mas seu argumento aumenta de ^?/₂.

Em decorrência, ao multiplicarmos por i todos os pontos da região indicada, ela manterá seu tamanho, mas sofrerá uma rotação de 90º, (...).?

Obs.: esta é uma questão que verifica se o professor está utilizando os cadernos enviados pelo governo ou se está seguindo a proposta curricular do governo.

Fonte: São Paulo (Estado) Secretaria da Educação. Material de apoio ao Currículo do Estado de São Paulo ? Caderno do Professor de Matemática ? Ensino Médio ? 3° Ano. São Paulo: SEE, 2014.

***

Professor compartilhe sua criatividade!

Compartilhe esta ideia de divulgar a Matemática!

POSTAR UM COMENTÁRIO

- Questão 55 ? Processo De Promoção ? Qm ? Professor De Matemática ? See/sp ? 2.015
Em um dos Cadernos do Professor da Secretaria da Educação do Estado de São Paulo, da 3ª série do Ensino Médio, há um destaque para o estudo das cônicas. Nesse caderno, as cônicas são apresentadas e caracterizadas por meio de propriedades...

- Questão 50 ? Processo De Promoção ? Qm ? Professor De Matemática ? See/sp ? 2.015
Os conteúdos disciplinares de Matemática do Currículo da Secretaria da Educação do Estado de São Paulo para o Ensino Fundamental II e Ensino Médio estão organizados segundo os blocos temáticos: (A) Números e Operações; Espaço e Forma; Grandezas...

- Questão 44 ? Processo De Promoção ? Qm ? Professor De Matemática ? See/sp ? 2.015
Os Cadernos do Professor da Secretaria da Educação do Estado de São Paulo apresentam antes de cada Situação de Aprendizagem um quadro no qual constam as estratégias, competências e habilidades relacionadas àquela situação. Considere as competências...

- Uma Aplicação Dos Números Complexos à Geometria
Nesta postagem queremos apresentar alguns fatos sobre números complexos a fim de podermos resolver o problema do tesouro. O ponto crucial é como utilizar os números complexos para rotacionar um vetor segundo um ângulo de 90º. Forma algébrica dos...

- Área De Uma Região Plana
Algumas regiões planas se assemelham a polígonos conhecidos como triângulo, quadrado, retângulo, losango, paralelogramo, trapézio, pentágono, hexágono, entre outros, onde cada um possui uma fórmula específica para determinar a área de sua superfície....

Matemática