Matemática
Semelhança de PolígonosIntrodução
Observe as figuras:
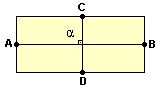


Dizemos que esse mapas são figuras semelhantes.
Nessas figuras podemos identificar:
AB - distância entre A e B (comprimento do retângulo)
CD - distância entre C e D (largura do retângulo)
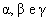 - ângulos agudos formados pelos segmentos
- ângulos agudos formados pelos segmentos 
Medindo os segmentos de reta e
e  e os ângulos (
e os ângulos (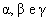 ) das figuras, podemos organizar a seguinte tabela:
) das figuras, podemos organizar a seguinte tabela:
Observe que:


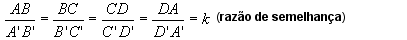


- Questão 36 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
É correto afirmar que são sempre semelhantes dois (A) quadriláteros cujos lados são respectivamente proporcionais. (B) quadriláteros cujos lados têm medidas iguais. (C) quadriláteros cujos ângulos internos são retos. (D) triângulos retângulos...
- Questão 36 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Seguem três afirmações sobre semelhança de polígonos: I. se os lados de dois triângulos são respectivamente paralelos dois a dois, então esses triângulos são semelhantes; II. todos os losangos que têm as medidas das duas diagonais iguais entre...
- Questão 36 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Analise as três afirmações sobre semelhança de polígonos. I. Dois quadrados são sempre semelhantes. II. Se os ângulos de dois quadriláteros são respectivamente congruentes, então eles são semelhantes. III. Se os ângulos de dois...
- Semelhança De Polígonos
Polígonos são regiões planas fechadas, constituídas de lados, vértices e ângulos. Dizemos que dois polígonos são semelhantes quando eles possuem o mesmo número de lados e se adéquam às seguintes condições: Ângulos iguais. Lados correspondentes...
- Semelhança De Triângulos
Identificando dois triângulos semelhantesSabemos que triângulos são polígonos. Sendo assim, o estudo que é feito para identificar a semelhança defiguras poligonais será válido para o estudo da semelhança de triângulos. Com isso, dois triângulos...
Matemática
Semelhança de Polígonos
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
www.accbarrosogestar.wordpress.com
Semelhança de Polígonos
Observe as figuras:

Figura A

Figura B

Figura C
Elas representam retângulos com escalas diferentes. Observe que os três retângulos tem a mesma forma, mas de tamanhos diferentes.Dizemos que esse mapas são figuras semelhantes.
Nessas figuras podemos identificar:
AB - distância entre A e B (comprimento do retângulo)
CD - distância entre C e D (largura do retângulo)
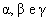 - ângulos agudos formados pelos segmentos
- ângulos agudos formados pelos segmentos 
Medindo os segmentos de reta
 e
e  e os ângulos (
e os ângulos (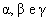 ) das figuras, podemos organizar a seguinte tabela:
) das figuras, podemos organizar a seguinte tabela:m ( ) ) | m ( ) ) | ângulo | |
| Fig. C | 3,9 cm | 1,3 cm | 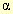 = 90º = 90º |
| Fig. B | 4,5 cm | 1,5 cm | 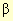 = 90º = 90º |
| Fig. A | 6,0 cm | 2,0 cm |  = 90º = 90º |
- Os ângulos correspondente nas três figuras têm medidas iguais;
- As medidas dos segmentos correspondentes são proporcionais;
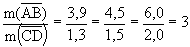
Desse exemplo, podemos concluir que duas ou mais figuras são semelhantes em geometria quando:
- os ângulos correspondentes têm medidas iguais ;
- as medidas dos segmentos correspondentes são proporcionais;
- os elementos das figuras são comuns.
Outro exemplos de figuras semelhantes:



têm formas iguais e tamanhos diferentes.
Polígonos Semelhantes
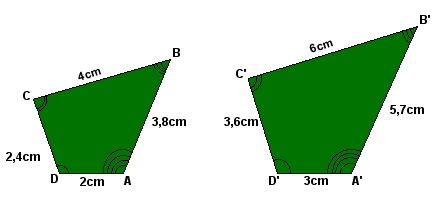
Considere os polígonos ABCD e A'B'C'D', nas figuras:

Observe que:
- os ângulos correspondentes são congruentes:

- os lados correspondentes (ou homólogos) são proporcionais:
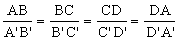
ou
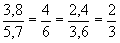
Podemos concluir que os polígonos ABCD e A'B'C'D' são semelhantes e indicamos:
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")
Ou seja:
| Dois polígonos são semelhantes quando os ângulos correspondentes são congruentes e os lados correspondentes são proporcionais. |
A razão entre dois lados correspondentes em polígonos semelhante denomina-se razão de semelhança, ou seja:
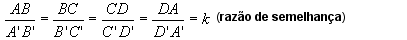
A razão de semelhança dos polígonos considerados é 

Obs: A definição de polígonos semelhantes só é válida quando ambas as condições são satisfeitas: Ângulos correspondentes congruentes e lados correspondentes proporcionais. Apenas uma das condições não é suficiente para indicar a semelhança entre polígonos.
Propriedades
| Se dois polígonos são semelhantes, então a razão entre seus perímetros é igual à razão entre as medidas de dois lados homólogos quaisquer dos polígonos. |
Demonstração:
Sendo ABCD ~ A'B'C'D', temos que:


Os perímetros desses polígonos podem ser assim representados:
Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:

Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:

Exemplo:
- Os lados de um triângulo medem 3,6 cm, 6,4 cm e 8 cm. Esse triângulo é semelhante a um outro cujo perímetro mede 45 cm. calcule os lados do segundo triângulo.
Solução
Razão de semelhança =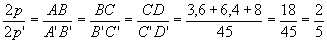

Razão de semelhança =
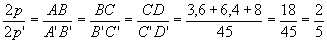

Logo, os lados do segundo triângulo são 9cm, 16cm e 20cm.
www.somatematica.com.br
- Questão 36 ? Processo De Promoção ? Professor De Matemática ? See ? São Paulo ? 2.013
É correto afirmar que são sempre semelhantes dois (A) quadriláteros cujos lados são respectivamente proporcionais. (B) quadriláteros cujos lados têm medidas iguais. (C) quadriláteros cujos ângulos internos são retos. (D) triângulos retângulos...
- Questão 36 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Seguem três afirmações sobre semelhança de polígonos: I. se os lados de dois triângulos são respectivamente paralelos dois a dois, então esses triângulos são semelhantes; II. todos os losangos que têm as medidas das duas diagonais iguais entre...
- Questão 36 ? Prova Do Estado ? (ofa) 2.012 ? Professor De Educação Básica Ii
Analise as três afirmações sobre semelhança de polígonos. I. Dois quadrados são sempre semelhantes. II. Se os ângulos de dois quadriláteros são respectivamente congruentes, então eles são semelhantes. III. Se os ângulos de dois...
- Semelhança De Polígonos
Polígonos são regiões planas fechadas, constituídas de lados, vértices e ângulos. Dizemos que dois polígonos são semelhantes quando eles possuem o mesmo número de lados e se adéquam às seguintes condições: Ângulos iguais. Lados correspondentes...
- Semelhança De Triângulos
Identificando dois triângulos semelhantesSabemos que triângulos são polígonos. Sendo assim, o estudo que é feito para identificar a semelhança defiguras poligonais será válido para o estudo da semelhança de triângulos. Com isso, dois triângulos...
