Matemática
CLASSIFICAÇÃO
Quanto à razão, as progressões aritméticas podem ser classificadas em:
1. Crescentes – São aquelas cuja razão é positiva.
Exemplo:
(4, 8, 12...) →r = 4 > 0 (positiva)
2. Decrescentes – São aquelas cuja razão é negativa.
Exemplo:
(10, 7, 4, 1, –2, –5)→ r = – 3 < 0 (negativa) 3. Constantes – São aquelas cuja razão é nula. Exemplo: (6, 6, 6, 6) →r = 0 FÓRMULA DO TERMO GERAL Para obter o enésimo termo de uma P.A., basta somar (n – 1) vezes a razão ao primeiro termo. Com isso, podemos achar qualquer termo dentro de uma PA pela expressão: an = a1 + (n - 1) . r Em que: an é o enésimo termo (termo geral); a1 é o primeiro termo; n é o número de termos; r é a razão. Aplicação Qual é o quinto termo da P. A. (3, 6...)? Solução: a1 = 3 r = 6 – 3 = 3 n = 5 an = a1 + (n - 1) . r a20 = 3 + (5 – 1). 3 a20 = 3 + 4.3 a20 = 15 INTERPOLAÇÃO ARITMÉTICA Interpolar ou inserir k meios aritméticos entre dois termos extremos a e b de uma progressão aritmética significa obter uma P. A. com (k + 2) termos.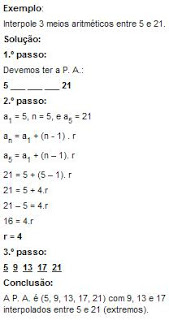
http://ensinodematemtica.blogspot.com
- Progressão Geometrica
Progressão geométrica é uma seqüencia numérica que cresce ou decresce pelo produto por uma taxa constante. Nessa progressão, os seus termos a partir do segundo é igual ao produto do termo anterior por uma constante denominada razão q. Por exemplo:...
- Progressão Aritmetica
O estudo sobre sequências numéricas desperta o conhecimento das Progressões Aritméticas ou Geométricas. As relações existentes nas progressões são estudadas e analisadas no intuito de descobrir termos, razão e soma de termos. Nosso estudo será...
- Progressão Aritmética
Definição: uma Progressão Aritmética (ou P.A.) é uma sequência numérica em que a diferença entre qualquer termo (a partir do 2º) e o termo anterior é sempre a mesma (constante). A essa constante...
- ProgressÃo AritimÉtica
DEFINÇÃO Consideremos a seqüência ( 2, 4, 6, 8, 10, 12, 14, 16). Observamos que, a partir do segundo termo, a diferença entre qualquer termo e seu antecessor é sempre a mesma: 4 – 2 = 6 – 4 = 10 – 8 = 14 – 12 = 16 – 14 = 2 Seqüências...
- Progressão Geométrica (p.g.)
Definição: uma sequência numérica é chamada de Progressão Geométrica (P.G.) se o quociente entre qualquer termo (a partir do 2º) e o termo antecessor for sempre o mesmo (constante). A essa constante...
Matemática
Sequências PA
CLASSIFICAÇÃO
Quanto à razão, as progressões aritméticas podem ser classificadas em:
1. Crescentes – São aquelas cuja razão é positiva.
Exemplo:
(4, 8, 12...) →r = 4 > 0 (positiva)
2. Decrescentes – São aquelas cuja razão é negativa.
Exemplo:
(10, 7, 4, 1, –2, –5)→ r = – 3 < 0 (negativa) 3. Constantes – São aquelas cuja razão é nula. Exemplo: (6, 6, 6, 6) →r = 0 FÓRMULA DO TERMO GERAL Para obter o enésimo termo de uma P.A., basta somar (n – 1) vezes a razão ao primeiro termo. Com isso, podemos achar qualquer termo dentro de uma PA pela expressão: an = a1 + (n - 1) . r Em que: an é o enésimo termo (termo geral); a1 é o primeiro termo; n é o número de termos; r é a razão. Aplicação Qual é o quinto termo da P. A. (3, 6...)? Solução: a1 = 3 r = 6 – 3 = 3 n = 5 an = a1 + (n - 1) . r a20 = 3 + (5 – 1). 3 a20 = 3 + 4.3 a20 = 15 INTERPOLAÇÃO ARITMÉTICA Interpolar ou inserir k meios aritméticos entre dois termos extremos a e b de uma progressão aritmética significa obter uma P. A. com (k + 2) termos.
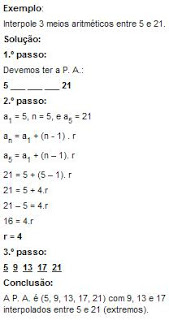
http://ensinodematemtica.blogspot.com
- Progressão Geometrica
Progressão geométrica é uma seqüencia numérica que cresce ou decresce pelo produto por uma taxa constante. Nessa progressão, os seus termos a partir do segundo é igual ao produto do termo anterior por uma constante denominada razão q. Por exemplo:...
- Progressão Aritmetica
O estudo sobre sequências numéricas desperta o conhecimento das Progressões Aritméticas ou Geométricas. As relações existentes nas progressões são estudadas e analisadas no intuito de descobrir termos, razão e soma de termos. Nosso estudo será...
- Progressão Aritmética
Definição: uma Progressão Aritmética (ou P.A.) é uma sequência numérica em que a diferença entre qualquer termo (a partir do 2º) e o termo anterior é sempre a mesma (constante). A essa constante...
- ProgressÃo AritimÉtica
DEFINÇÃO Consideremos a seqüência ( 2, 4, 6, 8, 10, 12, 14, 16). Observamos que, a partir do segundo termo, a diferença entre qualquer termo e seu antecessor é sempre a mesma: 4 – 2 = 6 – 4 = 10 – 8 = 14 – 12 = 16 – 14 = 2 Seqüências...
- Progressão Geométrica (p.g.)
Definição: uma sequência numérica é chamada de Progressão Geométrica (P.G.) se o quociente entre qualquer termo (a partir do 2º) e o termo antecessor for sempre o mesmo (constante). A essa constante...
