Matemática

Solucionando o Problema do Gato e Rato (parte 1)

Nesta postagem começaremos a resolver o Problema do Gato e Rato.

Vamos chamar de a a distância inicial entre o gato e o rato e inserir um sistema de coordenadas cartesianas de forma que a origem do sistema coincida com a localização inicial do rato e de tal modo que a localização inicial do gato fique sobre eixo-x.

Nestas condições, no momento inicial, o rato estará localizado no ponto (0, 0) de nosso sistema de coordenadas enquanto que o gato estará no ponto (a, 0).

É claro que passado algum tempo, tanto o rato (que fugiu) quanto o gato (que perseguiu) possuem localizações diferentes de suas respectivas localizações iniciais. Afim de estudarmos o problema, consideremos passados t segundos a partir do instante inicial (isto é, a partir de t = 0).

Vamos chamar de (0, b) a localização do rato no instante t;
Vamos chamar de (z, w) a localização do gato no instante t;

Vamos chamar de f a função cujo gráfico é a curva descrita pelo gato;
Vamos chamar de g a função cujo gráfico é a reta que indica a direção em que o gato se desloca.

Observe que se chamarmos de k a distância que o rato percorreu até o instante t e de v a sua velocidade (que é constante) então obtemos k = vt. Olhando para a figura acima não é difícil ver que k = b, portanto podemos escrever b = vt. Mas olhando para a figura também vê-se claramente que g(0) = b, logo temos g(0) = vt.

Vamos calcular g(0). Para tanto lembremos que a equação de uma reta pode ser dada pela expressão g(x?) ? g(x) = m(x? ? x), onde (x? , g(x?)) é um ponto pertencente a reta e m é a sua inclinação (geralmente chamado de coeficiente angular). Neste caso, o ponto (z, w) pertence a reta, portanto podemos por x? = z e obter:

g(z) ? g(x) = m(z ? x)

w ? g(x) = m(z ? x)

g(x) = w ? m(z ? x)

Agora, para determinar m, consideremos o seguinte: quando o enunciado do problema diz que "o gato sempre corre na direção em que o rato está", ele está querendo dizer que esta direção é sempre tangente ao caminho do gato no ponto em que ele se encontra (em outros termos: no instante t, a reta azul é tangente à curva verde no ponto (z, w)). Segue-se, do Cálculo, que m = f '(z) e, portanto, podemos escrever g(x) = w ? f '(z)(z ? x). Pondo x = 0, obtemos, enfim, g(0) = w ? f '(z)z. Notando ainda que w = f(z), podemos escrever g(0) = f(z) ? f '(z)z. Em face disto, concluímos que:

f(z) ? f '(z)z = vt

Analogamente ao que fizemos no primeiro parágrafo após a segunda figura, se chamarmos de d a distância que o gato percorreu até o instante t e de u a sua velocidade (que também é constante) obtemos d = ut, donde segue que t = d/u. Deste modo: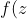

$f(z)-f'(z)z=v\;\frac{d}{u}=\frac{v}{u}\;d$

Notemos agora que d é o comprimento da curva verde, entre z e a. Segue-se, também do Cálculo, o seguinte resultado:

$d=\int_z^a\sqrt{1+[f'(x)]^2} \;\;dx=-\int_a^z\sqrt{1+[f'(x)]^2} \;\;dx$

Combinando as últimas duas igualdades, obtemos:

$f(z)-f'(z)z=-\frac{v}{u}\int_a^z\sqrt{1+[f'(x)]^2} \;\;dx$

Observe que z não é constante. De fato, por ser z o valor da abscissa do ponto que designa a posição do gato no instante t, ele depende do tempo (conforme o tempo muda a posição do gato também muda - e consequentemente o valor de z). Deste modo podemos olhar para z como sendo uma variável. Derivando, então, ambos os lados da última igualdade com relação à variável z obtemos:
$\frac{d}{dz}\left [f(z)-f'(z)z \right ]=\frac{d}{dz}\left [-\frac{v}{u}\int_a^z\sqrt{1+[f'(x)]^2} \;\;dx \right ]$
Regra da diferença no primeiro membro e regra da constante no segundo:
$\frac{d}{dz}\left [f(z) \right ]-\frac{d}{dz}\left [f'(z)z \right ]=-\frac{v}{u}\;\frac{d}{dz}\left [\int_a^z\sqrt{1+[f'(x)]^2} \;\;dx \right ]$
Regra do produto no primeiro membro e Teorema Fundamental do Cálculo no segundo:
$\frac{d}{dz}\left [f(z) \right ]-\left (f'(z)\frac{d}{dz}\left [z \right ]+z\frac{d}{dz}\left [f'(z) \right ] \right )=-\frac{v}{u}\;\sqrt{1+[f'(z)]^2}$
Regra básica de derivação e álgebra elementar no primeiro membro:

$\frac{d}{dz}\left [f(z) \right ]-f'(z)-z\frac{d}{dz}\left [f'(z) \right ] =-\frac{v}{u}\;\sqrt{1+[f'(z)]^2}$
Mudando a notação:

$f'(z)-f'(z)-zf''(z) =-\frac{v}{u}\;\sqrt{1+[f'(z)]^2}$
Simplificando a expressão:
$zf''(z) =\frac{v}{u}\;\sqrt{1+[f'(z)]^2}$
Temos, pois, uma equação diferencial de segunda ordem na variável z. O próximo passo é resolvê-la, tarefa esta que continua aqui.

Referências: na última postagem da série.
Relate erros aqui.

Veja + sobre EDO:

Parte 1 / Parte 2 / Parte 3 / Parte 4 (separáveis)

Parte 1 (homogênias)

- O Peso De Um Elefante é Igual Ao Peso De Um Rato?
Se x é do peso de um elefante, e y é o peso de um rato, consideremos a soma dos dois pesos de 2? v, então, matematicamente: x + y = 2 ? v ...

- Questão 55 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Na figura mostrada a seguir, é apresentado um trecho da reta numérica. Os pontos destacados dividem o segmento de reta em intervalos de tamanhos iguais. Se x +2 é o número real correspondente ao ponto K, é correto afirmar que o valor de x é (A)...

- Solucionando O Problema Do Gato E Rato (parte 2)
Em postagem anterior, analisamos o problema e concluímos que o próximo passo seria resolver a seguinte equação diferencial:Observemos, inicialmente, que o valor de f em a é 0, ou seja, f(a) = 0. Isto é fácil ver, basta olhar para a figura: Além...

- Noções De Lógica - Exercícios Resolvidos
Noções de Lógica - Exercícios resolvidos 01. Sendo p a proposição Paulo é paulista e q a proposição Ronaldo é carioca, traduzir para a linguagem corrente as seguintes proposições: a) ~q b) p ^ q c) p v q d) p " q e) p " (~q) RESOLUÇÃO:...

- Equação Fundamental Da Reta
Com um ponto e um ângulo podemos indicar e construir uma reta. E se a reta formada não for vertical (reta vertical é perpendicular ao eixo Ox) com o ponto pertencente a ela mais o seu coeficiente angular (tangente do ângulo de inclinação) é possível...

Matemática