Matemática
- Construção Geométrica De Phi Em Circunferências (parte 8)
Esta construção foi elaborada por Jo Niemeyr e publicada no Forum Geometricorum, volume 11 de 2011. 1) Para esta construção, inicie com uma circunferência de dentro D e diâmetro AB. 2) Trace uma reta tangente ao ponto A, prolongando-a. 3) Descreva...
- Construção Geométrica De Phi Em Circunferências (parte 7)
Esta construção foi elaborada por Michael Bataille e publicada no Forum Geometricorum em 2011. Seja um triângulo equilátero ABC, onde em um de seus lados, externamente, construa um quadrado, cujos lados também serão de comprimento AB. Com centro...
- Construção Geométrica De Phi Em Circunferências (parte 6)
Esta construção geométrica de PHI foi elaborada por Kurt Hofsteller, em 5 passos utilizando apenas régua e compasso. [Figura 1] Construção: 1) Descreva uma circunferência C1 de raio AB com centro em A; 2) Descreva uma circunferência C2 de raio...
- Construção Geométrica De Phi Em Circunferências (parte 2)
Esta é uma construção com três circunferências concêntricas, cujos raios estão numa proporção de 1 : 2 : 4, onde podemos encontrar a razão áurea: Sejam três circunferências concêntricas de raios 1, 2 e 4. Traçar uma tangente à circunferência...
- Construção Geométrica De Phi Em Circunferências (parte 1)
Há diversas construções geométricas utilizando circunferências onde podemos encontrar a constante Φ (PHI), ou o número de ouro. Sejam três circunferências de diâmetros iguais a 1, cujos centros são colineares e tangentes entre si duas a duas....
Matemática
Construção Geométrica de PHI em Circunferências (Parte 5)
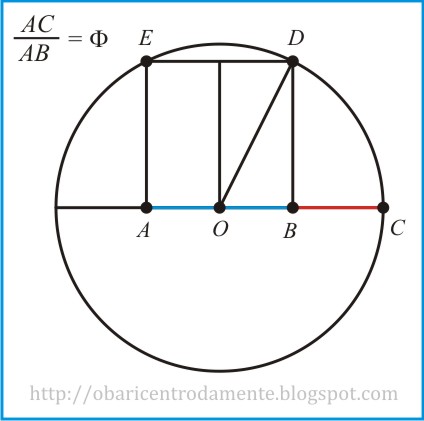
Esta talvez seja a construção mais conhecida da Razão Áurea e consiste em inscrever um quadrado numa semicircunferência. A razão entre os segmentos AC e AB é a Razão Áurea.

Como já temos o segmento AB, vamos escrever o segmento AC em função de AB. Como o quadrilátero ABDE é um quadrado por construção, temos que AB = BD. Pelo teorema pitagórico, temos que:





Vejam que o segmento AC = OC + AO. Desta forma temos:



Veja mais:
Construções Geométrica de PHI em Circunferências (Parte 1)
Construções Geométrica de PHI em Circunferências (Parte 2)
Construções Geométrica de PHI em Circunferências (Parte 3)
Construções Geométrica de PHI em Circunferências (Parte 4)
Construções Geométrica de PHI em Circunferências (Parte 1)
Construções Geométrica de PHI em Circunferências (Parte 2)
Construções Geométrica de PHI em Circunferências (Parte 3)
Construções Geométrica de PHI em Circunferências (Parte 4)
- Construção Geométrica De Phi Em Circunferências (parte 8)
Esta construção foi elaborada por Jo Niemeyr e publicada no Forum Geometricorum, volume 11 de 2011. 1) Para esta construção, inicie com uma circunferência de dentro D e diâmetro AB. 2) Trace uma reta tangente ao ponto A, prolongando-a. 3) Descreva...
- Construção Geométrica De Phi Em Circunferências (parte 7)
Esta construção foi elaborada por Michael Bataille e publicada no Forum Geometricorum em 2011. Seja um triângulo equilátero ABC, onde em um de seus lados, externamente, construa um quadrado, cujos lados também serão de comprimento AB. Com centro...
- Construção Geométrica De Phi Em Circunferências (parte 6)
Esta construção geométrica de PHI foi elaborada por Kurt Hofsteller, em 5 passos utilizando apenas régua e compasso. [Figura 1] Construção: 1) Descreva uma circunferência C1 de raio AB com centro em A; 2) Descreva uma circunferência C2 de raio...
- Construção Geométrica De Phi Em Circunferências (parte 2)
Esta é uma construção com três circunferências concêntricas, cujos raios estão numa proporção de 1 : 2 : 4, onde podemos encontrar a razão áurea: Sejam três circunferências concêntricas de raios 1, 2 e 4. Traçar uma tangente à circunferência...
- Construção Geométrica De Phi Em Circunferências (parte 1)
Há diversas construções geométricas utilizando circunferências onde podemos encontrar a constante Φ (PHI), ou o número de ouro. Sejam três circunferências de diâmetros iguais a 1, cujos centros são colineares e tangentes entre si duas a duas....
