Matemática
(A) 1/20.
(B) 1/16.
(C) 1/12.
(D) 1/10.
(E) 1/8.
1º método de resolução:
Considerando os triângulos NCD e NIC temos: o ângulo NCI é côngruo ao ângulo NDC; o ângulo DNC é côngruo ao ângulo INC (este ângulo é comum aos triângulos NCD e NIC).
2º método de resolução:
Baseado na resolução de Elcioschin (http://www.soensino.com.br/foruns/viewtopic.php?f=5&t=28490).
Coloque o quadrado num sistema cartesiano de ponto (x,y) com os pontos dos vértices do quadrado em D(0, 0), C(1, 0), M(1/2, 1) e N(1, 1/2)
Resolução a pedido da Profª. Cleonice.
- Questão 46 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
O eneágono da figura é regular e o ponto O é o centro desse polígono. A medida do ângulo OAB, assinalado na figura, é (A) 45°. (B) 60°. (C) 70°. (D) 75°. (E) 80°. Solução: (C) Aplicando o Método de Resolução de Problemas segundo...
- Questão 40 ? Concurso See ? 2.010 ? Professor De Educação Básica Ii ? Matemática
Com relação à figura abaixo, sabe-se que: ? A, B, C, D são pontos pertencentes à reta r; ? E, F, G são pontos pertencentes à reta s; ? r é paralela à s; ? EF=FG=2.AB=2.BC=2.CD=2; ? dos sete pontos, os únicos pares de pontos alinhados verticalmente...
- Questão 50 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
A figura indica uma mesa de tampo AB (paralelo ao solo), pernas AE e BD, e pivô de fixação em C, que é deslizante ao longo de BD. Se AE = BD = 1 m, e o ângulo entre AE e BD, em graus, mede ?, então, a altura da mesa em relação ao solo, em metros,...
- Questão 36 ? Formação Básica Do Professor E Formação Específica Do Professor ? 2.007 ? Estado De São Paulo
Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfí-cie. Na figura, os ângulos ABC e BCD medem, respectiva-mente, 90º...
- Geométria Plana Resumo
1) Ângulos em retas paralelas 2) Triângulos # Classificação: Equilátero 3 lados iguais. Isósceles 2 lados iguais. Escaleno 3 lados desiguais. # Ângulos: A soma dos ângulos internos de um triângulo é igual a 180º. A soma dos ângulos externos...
Matemática
Questão 66 ? Formação Básica do Professor e Formação Específica do Professor ? 2.007 ? Estado de São Paulo
Seja ABCD um quadrado de lado unitário. Sendo M e N os pontos médios dos lados AB e BC, respectivamente, e I a in-tersecção dos segmentos DN e CM, a área do triângulo NIC é
(A) 1/20.
(B) 1/16.
(C) 1/12.
(D) 1/10.
(E) 1/8.
Solução: (A)
Seguindo os dados do exercício obtemos a figura:
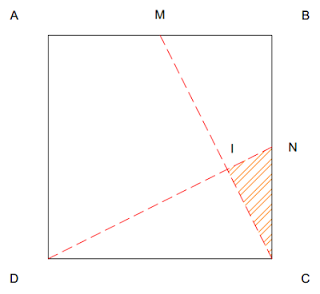 |
| Figura 1: Cosntrução obtida conforme os dados do problema. |
1º método de resolução:
Considerando os triângulos NCD e NIC temos: o ângulo NCI é côngruo ao ângulo NDC; o ângulo DNC é côngruo ao ângulo INC (este ângulo é comum aos triângulos NCD e NIC).
Portanto, pelo critério de dois ângulos congruente os triângulos NCD e NIC são semelhantes, assim, o ângulo NIC é reto (90º).
No triângulo NCD, reto em C, temos: NC = 1 / 2 e CD = 1, pelo Teorema de Pitágoras determina-se DN:
DN2 = NC2 + CD2 = 12 + (1 / 2)2
DN2 = 1 + (1 / 4) = 5 / 4
DN = ? (5 / 4) = (? 5) / 2
Utilizando a razão de semelhança sabemos que:
DN / NC = CD / IC
[(? 5) / 2] / (1 /2) = 1 / IC
IC = 1 / ?5
DN / NC = NC / NI
[(? 5) / 2] / (1 /2) = (1 / 2) / NI
NI = 1 / (2 ? ? 5)
A área do triângulo é o metade do produto da base pela altura.
Atriângulo= (IC ? NI) / 2
Atriângulo= {[1 / ?5] ? [1 / (2 ? ? 5)]} / 2 = {1 / [2 ? (? 5)2]} / 2 =
Atriângulo= {1 / 10} / 2 = 1 / 20
2º método de resolução:
Baseado na resolução de Elcioschin (http://www.soensino.com.br/foruns/viewtopic.php?f=5&t=28490).
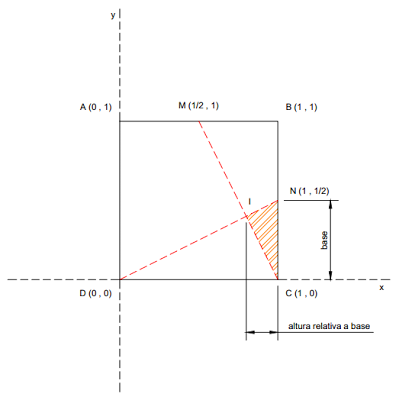 |
| Figura 2: Quadrado inserido no plano cartesiano. |
Coloque o quadrado num sistema cartesiano de ponto (x,y) com os pontos dos vértices do quadrado em D(0, 0), C(1, 0), M(1/2, 1) e N(1, 1/2)
Na geometria analítica podemos determinar a reta que passa por dois pontos:
Reta DN ? y = x / 2
Reta CM ? y = (? 2) ? (x ? 1) ? y = ? 2x + 2
As coordenadas do ponto I são obtidas igualando as equações da reta DN e da reta CM:
I ? x / 2 = ? 2x + 2 ? xI = 4 / 5 ? yI = 2 / 5
I (4 / 5, 2 / 5)
Base do triângulo = NC = 1/2
Altura do triângulo relativa à esta base é obtida calculando a distância entre a abscissa do ponto C e do ponto I
xC? xI = 1 ? 4 / 5 = 1 / 5
S = [(1 / 2) ? (1 / 5)] / 2 ? S = 1 / 20
Resolução a pedido da Profª. Cleonice.
- Questão 46 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
O eneágono da figura é regular e o ponto O é o centro desse polígono. A medida do ângulo OAB, assinalado na figura, é (A) 45°. (B) 60°. (C) 70°. (D) 75°. (E) 80°. Solução: (C) Aplicando o Método de Resolução de Problemas segundo...
- Questão 40 ? Concurso See ? 2.010 ? Professor De Educação Básica Ii ? Matemática
Com relação à figura abaixo, sabe-se que: ? A, B, C, D são pontos pertencentes à reta r; ? E, F, G são pontos pertencentes à reta s; ? r é paralela à s; ? EF=FG=2.AB=2.BC=2.CD=2; ? dos sete pontos, os únicos pares de pontos alinhados verticalmente...
- Questão 50 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
A figura indica uma mesa de tampo AB (paralelo ao solo), pernas AE e BD, e pivô de fixação em C, que é deslizante ao longo de BD. Se AE = BD = 1 m, e o ângulo entre AE e BD, em graus, mede ?, então, a altura da mesa em relação ao solo, em metros,...
- Questão 36 ? Formação Básica Do Professor E Formação Específica Do Professor ? 2.007 ? Estado De São Paulo
Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfí-cie. Na figura, os ângulos ABC e BCD medem, respectiva-mente, 90º...
- Geométria Plana Resumo
1) Ângulos em retas paralelas 2) Triângulos # Classificação: Equilátero 3 lados iguais. Isósceles 2 lados iguais. Escaleno 3 lados desiguais. # Ângulos: A soma dos ângulos internos de um triângulo é igual a 180º. A soma dos ângulos externos...
