Matemática

Questão 75 ? Prova do Estado ? (OFA) 2.014 ? Professor de Educação Básica II

Analise a seguir a resolução da inequação

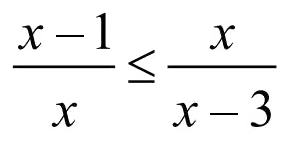
onde se conclui que x ? 3/4.

Analisando a resolução da inequação apresentada, é correto afirmar que

(A) todas as passagens e a conclusão estão corretas.

(B) a passagem de (I) para (II) está incorreta, o que compromete o resto da resolução.

(D) a passagem de (III) para (IV) está incorreta, o que compromete o resto da resolução.

(E) a passagem de (VII) para (VIII) está incorreta, o que se faz chegar a uma conclusão incorreta.

Solução: (D)

Aplicando o Método de Resolução de Problemas segundo Polya:

1° ? Compreensão do Problema

Quando temos a incógnita no denominador de uma inequação, costumamos classifica-la como uma inequação quociente.

Neste tipo de inequação é muito importante lembrar que não existe denominador nulo então x ? 0, pois de outra forma teríamos um denominador nulo na fração (x ? 1) / x, pelo mesmo motivo x ? 3, pois de outra forma teríamos um denominador nulo na fração x / (x ? 3).

A conclusão x ? 3/4 (lê se: ?x é maior que 3/4? ou ?x é maior que 0,75?) inclui o 3 na solução o que não é correto.

2° ? Estabelecimento de um Plano

Na análise inicial concluímos que a resolução está incorreta então devemos verificar onde está o erro.

3° ? Execução do Plano

Verificando onde está o erro:

(I)

x ? 1	?	x
x	?	x ? 3

(II)

(x ? 1) · (x ? 3)	?	x · x
x · (x ? 3)	?	x · (x ? 3)

(III)

x² ? 4 · x + 3	?	x²
x · (x ? 3)	?	x · (x ? 3)

(IV)

x² ? 4 · x + 3	?	x²	?	0
x · (x ? 3)		x · (x ? 3)

(V)

? 4 · x + 3	?	0
x · (x ? 3)

Observe que o erro esta na passagem do passo (III) para o passo (IV) quando realizou o procedimento de cancelar os denominadores, apenas realizamos esta operação quando temos uma equação, em inequações cuja solução é muitas vezes um intervalo de números no qual pode conter um ou mais números que não são soluções.

4° ? Avaliação

Questões envolvendo inequações ou equações quociente sempre envolve uma restrição pela própria característica da fração de representar uma divisão e não permitir o denominar nulo.

Prosseguindo com a resolução teríamos que realizar o estudo dos sinais para a equação do numerador e do denominador

Na equação do numerador: ? 4 · x + 3, sabemos que a raiz desta equação é x = 3/4, sabemos também que é uma equação decrescente, pois o coeficiente que acompanha o x (? 4) é negativo.

Esta equação gera como gráfico uma reta que cruza o eixo das abscissas no ponto de x = 3/4, então segundo o estudo de sinais para valores anteriores a x = 3/4 são positivos e para valores posteriores a x = 3/4 são negativos.

Na equação do numerador: x · (x ? 3), sabemos que as raízes desta equação é x = 0 e x = 3, sabemos também que é uma equação do segundo grau x · (x ? 3) = x² ? 3 · x, com a concavidade voltada para cima, pois o coeficiente que acompanha o x² é positivo.

Esta equação gera como gráfico uma parábola que cruza o eixo das abscissas nos pontos de x = 0 e de x = 3, então segundo o estudo de sinais para valores anterior a x = 0 são positivos, para valores entre x = 0 e x = 3 são negativos e para valores posteriores a x = 3 são positivos.

		0		3/4		3
?4 · x + 3		+	+	+	?	?	?
x · (x ? 3)		+	?	?	?	?	+
	?4 · x + 3	+	?	?	+	+	?
	x · (x ? 3)

A solução então é x < 0 e 3/4 ? x < 3.

- Questão 51 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
O gráfico a seguir representa uma função polinomial do 2.º grau. Analisando-se as informações do gráfico, é correto afirmar que a função representada é dada por: (A) y = x2+ 5x + 4. (B) y = x2? 4x + 5. (C) y = ? x2 ? 5x ? 4. (D) y = ?...

- Questão 49 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
A equação x2 + (y ? 1)2 = 25 representa uma (A) circunferência. (B) elipse. (C) hipérbole. (D) parábola. (E) reta. Solução: (A) Aplicando o Método de Resolução de Problemas segundo Polya: 1° ? Compreensão do Problema Segundo a teoria...

- Questão 41 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Os pares ordenados (0, 0) e (1, 3) pertencem ao gráfico de uma função polinomial do 2.º grau. O máximo dessa função tem abscissa x = 2. Logo, o valor da função no ponto de abscissa x = ?1 é (A) 5.(B) 4.(C) 0.(D) ?4.(E) ?5. Solução: (E) Aplicando...

- Questão 52 ? Formação Básica Do Professor E Formação Específica Do Professor ? 2.007 ? Estado De São Paulo
Dados os conjuntosA = {x ? R : x2 < 1} e B = {x ? R : 1 / x < 2} pode-se afirmar que (A) A ? B = ]1/2 , 1[(B) A ? B = ] ?1 , 0[ È ]1/2 , 1[(C) A ? B = ] ?1...

- Questão 31 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Ao resolver a inequação 2x ? 3 / 2 ? (x + 2) (x ? 1) / x, um aluno concluiu que x ? 4 / 5 e para isso resolveu da forma como está descrita a seguir, de I a VI: Analisando a forma de resolver, pode-se afirmar que (A) todas as passagens e a conclusão...

Matemática