Matemática
Considere uma P.A. qualquer de razão r.
(a1, a2, a3, a4, a5, ...)
A soma dos n primeiros termos dessa P.A. será dada por:
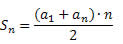
Onde,
a1 → é o primeiro termo da P.A.
an → é último termo a ser somado na P.A.
n → é o número de termos a serem somados na P.A.
Exemplo 1. Calcule a soma dos 20 primeiros termos da P.A. abaixo:
(5, 8, 11, 14, 17, ...)
Solução: Note que para a utilização da fórmula da soma dos termos é necessário conhecer o valor de a1 e a20. Temos que
a1 = 5; r = 8 – 5 = 3; n = 20;
Precisamos determinar qual é o 20º termo dessa P.A., ou a20. Para isso, iremos utilizar a fórmula do termo geral.
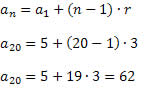
Agora, podemos utilizar a fórmula da soma dos n primeiros termos da P.A.
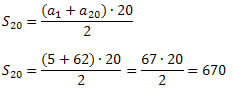
Exemplo 2. Calcule a soma dos 50 primeiros números naturais ímpares.
Solução: (1, 3, 5, 7, ...) é a sequência dos números ímpares. É fácil ver que a1 = 1 e r = 2. Precisamos determinar o 50º termo dessa sequência (a50). Para isso, iremos utilizar a fórmula do termo geral.
a50 = 1 + (50 - 1)∙2 = 1 + 49∙2 = 99
Agora podemos utilizar a fórmula da soma dos n primeiros termos da P.A.
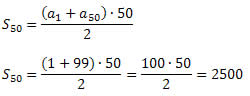
Exemplo 3. O primeiro termo de uma P.A. vale 0,7 e a soma de seus vinte primeiros termos é igual a 71. Determine o vigésimo termo dessa P.A.
Solução: Temos que
a1 = 0,7 S20 = 71 a20 = ?
Para solução desse problema devemos utilizar a fórmula da soma dos n primeiros termos de uma P.A.
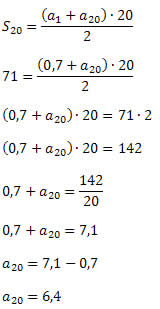
- Pa E Pg
Exercícios com PA e PG 1. Calcule a razão da P.G. onde a1 = e a8 = 48. 2. Em uma P.G. crescente tem-se a2 = 576. Calcule a razão e o 1º termo. 3. Sabendo que em uma P.G. a2 + a4 = 60 e a3 + a5 = 180, calcule a6 . 4. Somando o 1º termo com...
- Progressão Aritmética Propriedades
PROPRIEDADES DAS PROGRESSÕES ARITMÉTICAS 1.a propriedade (termos eqüidistantes dos extremos) Numa P.A. finita, de dois termos eqüidistantes dos extremos é igual à soma dos extremos. Exemplo: Seja a P. A. (8, 10, 12, 14, 16). Observa-se que: Os termos...
- Soma Dos Termos De Uma Progressão Aritmética
Considere (a1, a2, a3, ..., an) como sendo uma P.A. de razão r. A soma dos n primeiros termos dessa P.A. será dada por: Onde, a1 → é o primeiro termo da P.A. n → é o número de termos a serem somados an → é o último termo a ser somado Vamos...
- Progressão Aritmética
Marcos Noé P.AA sequência numérica que envolve números reais em que a partir do 2º elemento a diferença entre qualquer termo e seu antecessor seja um número constante recebe o nome de Progressão Aritmética...
- Soma Dos Termos De Uma Progressão Geométrica Finita
Onde a1 → é o primeiro termo da P.G. q → é a razão da P.G. n → é o número de termos Vamos fazer alguns exemplos para entender o uso correto da fórmula acima. Exemplo 1. Considere a P.G. (3, 6, 12, 24, ...). Determine a soma dos 15 primeiros...
Matemática
Soma dos termos de uma P.A
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email [email protected]
Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com
http://accbarrosogestar.blogspot.com.br
Extraído de http://www.alunosonline.com.br
Soma dos termos de uma P.A.
Marcelo RigonattoP.A.
(a1, a2, a3, a4, a5, ...)
A soma dos n primeiros termos dessa P.A. será dada por:
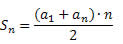
Onde,
a1 → é o primeiro termo da P.A.
an → é último termo a ser somado na P.A.
n → é o número de termos a serem somados na P.A.
Exemplo 1. Calcule a soma dos 20 primeiros termos da P.A. abaixo:
(5, 8, 11, 14, 17, ...)
Solução: Note que para a utilização da fórmula da soma dos termos é necessário conhecer o valor de a1 e a20. Temos que
a1 = 5; r = 8 – 5 = 3; n = 20;
Precisamos determinar qual é o 20º termo dessa P.A., ou a20. Para isso, iremos utilizar a fórmula do termo geral.
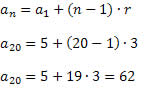
Agora, podemos utilizar a fórmula da soma dos n primeiros termos da P.A.
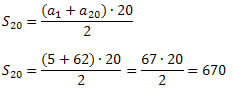
Exemplo 2. Calcule a soma dos 50 primeiros números naturais ímpares.
Solução: (1, 3, 5, 7, ...) é a sequência dos números ímpares. É fácil ver que a1 = 1 e r = 2. Precisamos determinar o 50º termo dessa sequência (a50). Para isso, iremos utilizar a fórmula do termo geral.
a50 = 1 + (50 - 1)∙2 = 1 + 49∙2 = 99
Agora podemos utilizar a fórmula da soma dos n primeiros termos da P.A.
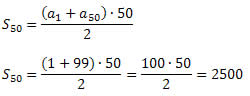
Exemplo 3. O primeiro termo de uma P.A. vale 0,7 e a soma de seus vinte primeiros termos é igual a 71. Determine o vigésimo termo dessa P.A.
Solução: Temos que
a1 = 0,7 S20 = 71 a20 = ?
Para solução desse problema devemos utilizar a fórmula da soma dos n primeiros termos de uma P.A.
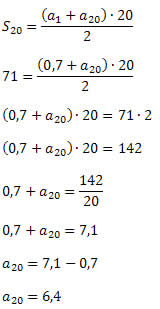
- Pa E Pg
Exercícios com PA e PG 1. Calcule a razão da P.G. onde a1 = e a8 = 48. 2. Em uma P.G. crescente tem-se a2 = 576. Calcule a razão e o 1º termo. 3. Sabendo que em uma P.G. a2 + a4 = 60 e a3 + a5 = 180, calcule a6 . 4. Somando o 1º termo com...
- Progressão Aritmética Propriedades
PROPRIEDADES DAS PROGRESSÕES ARITMÉTICAS 1.a propriedade (termos eqüidistantes dos extremos) Numa P.A. finita, de dois termos eqüidistantes dos extremos é igual à soma dos extremos. Exemplo: Seja a P. A. (8, 10, 12, 14, 16). Observa-se que: Os termos...
- Soma Dos Termos De Uma Progressão Aritmética
Considere (a1, a2, a3, ..., an) como sendo uma P.A. de razão r. A soma dos n primeiros termos dessa P.A. será dada por: Onde, a1 → é o primeiro termo da P.A. n → é o número de termos a serem somados an → é o último termo a ser somado Vamos...
- Progressão Aritmética
Marcos Noé P.AA sequência numérica que envolve números reais em que a partir do 2º elemento a diferença entre qualquer termo e seu antecessor seja um número constante recebe o nome de Progressão Aritmética...
- Soma Dos Termos De Uma Progressão Geométrica Finita
Onde a1 → é o primeiro termo da P.G. q → é a razão da P.G. n → é o número de termos Vamos fazer alguns exemplos para entender o uso correto da fórmula acima. Exemplo 1. Considere a P.G. (3, 6, 12, 24, ...). Determine a soma dos 15 primeiros...
